69. x 的平方根

题目：

69. x 的平方根

题解：

1. 题解一：暴力法(实用)

暴力循环即可。

2. 题解二：二分法(优选)

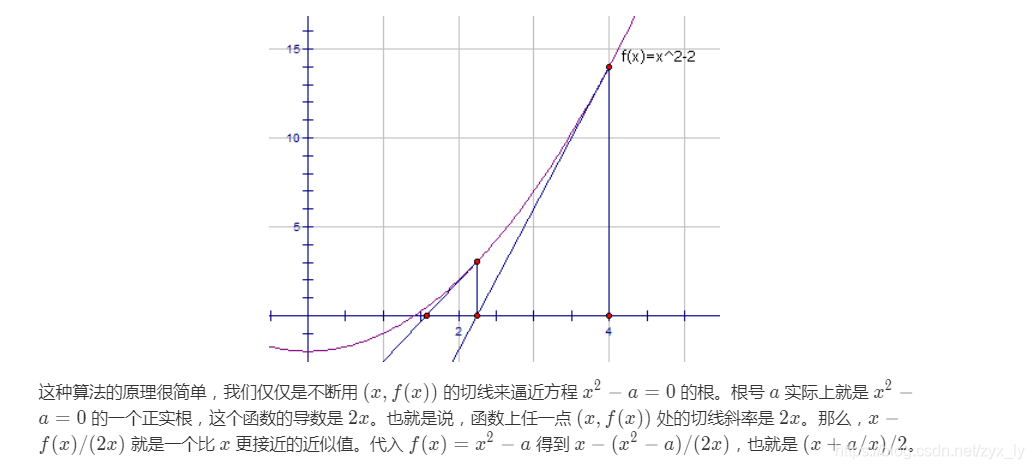
3. 题解三：牛顿法(技巧)

代码：

1. 代码一：暴力法(实用)

import java.util.Scanner;

public class lc_69 {

    public static int mySqrt(int x) {
        long ans = 0;
        for(long i = 0; i <= Math.sqrt(x); i++)
        {
            if(i * i <= x && (i + 1) * (i + 1) > x)
            {
                ans = i;
            }
        }
        return (int)ans;
    }

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        while (sc.hasNextInt()) {
            int x = sc.nextInt(); // x == 2147395600
            int res = mySqrt(x); // res == 46340
            System.out.println(res);
        }
        sc.close();
    }
}

2. 代码二：二分法(优选)

import java.util.Scanner;

public class lc_69_solution2 {

    public static int mySqrt(int x) {
        if (x == 0) {
            return 0;
        }
        long right = x;
        long left = 1;
        long mid;
        while (left <= right) {
            mid = left + (right - left) / 2;
            if (mid * mid > x) {
                right = mid - 1;
            } else if (mid * mid < x) {
                if ((mid + 1) * (mid + 1) > x) {
                    return (int) mid;
                }
                left = mid + 1;
            } else if (mid * mid == x) {
                return (int) mid;
            }
        }
        return (int) left;
    }

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        while (sc.hasNextInt()) {
            int x = sc.nextInt(); // x == 2147395600
            int res = mySqrt(x); // res == 46340
            System.out.println(res);
        }
        sc.close();
    }
}

3. 代码三：牛顿法(技巧)

/**
 * code69
 */
import java.util.*;

public class code69 {

    // x = (x + a / x) / 2
    public static int mySqrt(int x) {
        long res = x;
        while (res * res > x) {
            res = (res + x / res) / 2;
        }
        return (int) res;
    }

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        while (sc.hasNextInt()) {
            int x = sc.nextInt(); // x == 2147395600
            int res = mySqrt(x); // res == 46340
            System.out.println(res);
        }
        sc.close();
    }
}

参考：

1. 二分查找 + 牛顿法（Python 代码、Java 代码）
2. 牛顿迭代法
3. 牛顿迭代法
4. 牛顿法与拟牛顿法