进阶算法04

无后效性问题：

• 不管通过什么方式到达某个状态，其返回值都一样。

1. 换钱的方法数

暴力递归

• 以arr = [5, 10, 25, 1]，aim = 15为例：
  
  节点中的内容表示：
  • 从下标为[i~j]的数组中取任意张，可以换到aim的方法数

class Solution{

public:
    int coins(int *arr, int len, int aim)
    {
        if (!arr || len == 0 || aim < 0)
            return 0;
            
        return help(arr, len, 0, aim);
    }

private:
    //从下标为[index~len-1]的数组中取任意张，可以换到aim的方法数
    int help(int *arr, int len, int index, int aim)
    {
        int ret = 0;
        if (index == len)
            ret = (aim == 0) ? 1 : 0;
        else{
            for (int i = 0; arr[index] * i <= aim; i++)
            {
                ret += help(arr, len, index + 1, aim - arr[index] * i);
            }
        }

        return ret;
    }
};

可以发现 暴力递归 有许多重复性计算，可以使用记忆化搜索

class Solution{

public:
    int coins(int *arr, int len, int aim)
    {
        if (!arr || len == 0 || aim < 0)
            return 0;

        memo = vector<vector<int>>(len + 1, vector<int>(aim + 1, -1));

        return help(arr, len, 0, aim);
    }

private:
    vector<vector<int>> memo;       //memo[i][j]：从下标为[i...len-1]处选取任意张，可以换到j的方法数

    //从下标为[index~len-1]的数组中取任意张，可以换到aim的方法数
    int help(int *arr, int len, int index, int aim)
    {
        int ret = 0;
        if (index == len)
            ret = (aim == 0) ? 1 : 0;
        else{
            for (int i = 0; arr[index] * i <= aim; i++)
            {
                if (memo[index + 1][aim - arr[index] * i] != -1)
                    ret += memo[index + 1][aim - arr[index] * i];
                else
                    ret += help(arr, len, index + 1, aim - arr[index] * i);
            }
        }

        memo[index][aim] = ret;

        return ret;
    }
};

动态规划

从暴力递归的递归函数可以看出：

• 要计算当前（index，aim）的返回值，需要通过（index+1， aim-xxx）来获得

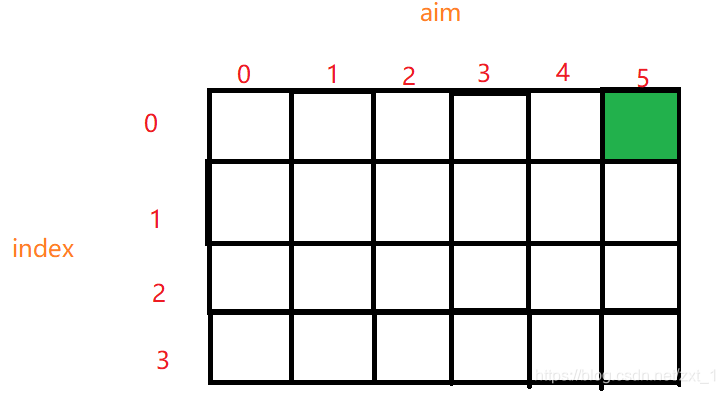
以arr=[5,3,2]，aim = 5为例

最终要求得绿色位置的值。

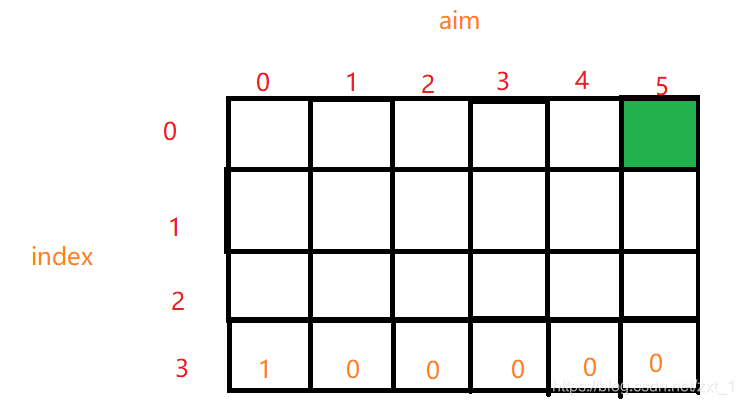
1.首先填写最后一排

2.依次往上填
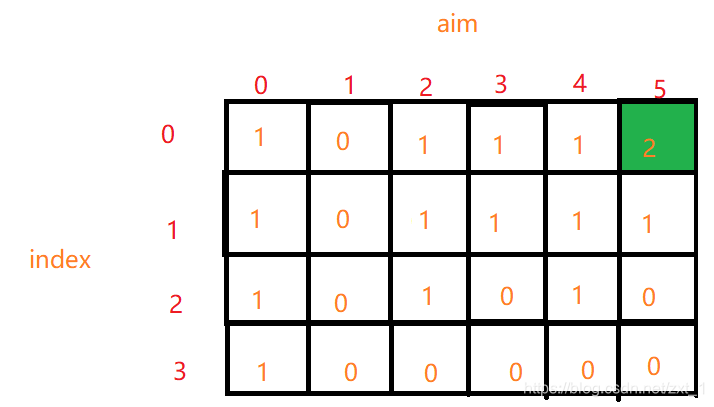
比如想计算 index=2,aim=4 的值：
memo[2][4] = memo[3][4] + memo[3][2] + memo[3][0]
(前一个是arr[2]取0张，中间是arr[2]取1张，后一个是arr[2]取2张）

• 最终结果：
  

class Solution{

public:
    int coins(int *arr, int len, int aim)
    {
        if (!arr || len == 0 || aim < 0)
            return 0;

        memo = vector<vector<int>>(len + 1, vector<int>(aim + 1, 0));

        memo[len][0] = 1;

        for (int i = len - 1; i >= 0; i--)
        {
            for (int j = 0; j <= aim; j++)
            {
                for (int k = 0; j - k*arr[i] >= 0; k++)
                    memo[i][j] += memo[i + 1][j - k*arr[i]];
            }
        }

        return memo[0][aim];
    }

private:
    vector<vector<int>> memo;       //memo[i][j]：从下标为[i...len-1]处选取任意张，可以换到j的方法数

};

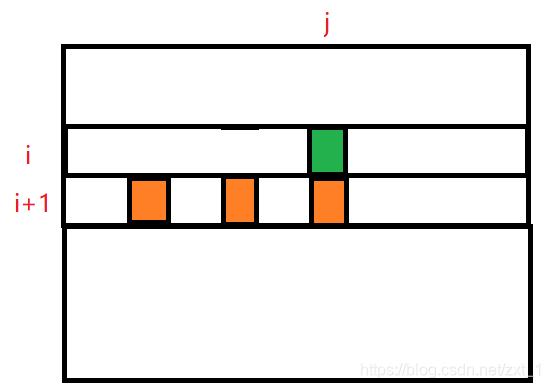
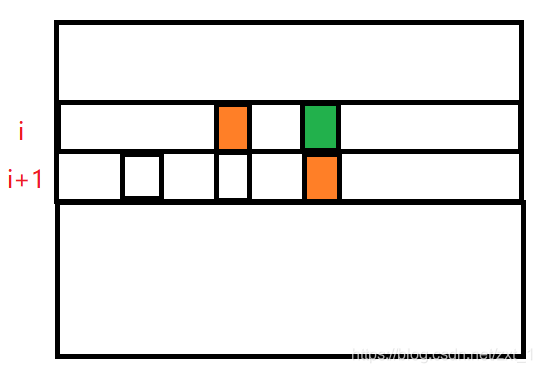
假设现在要计算 memo[i][j] 位置上的值，按照上述方法，要通过橙色方块求得。

• 优化：可以通过下图橙色方块求得
  

class Solution{

public:
    int coins(int *arr, int len, int aim)
    {
        if (!arr || len == 0 || aim < 0)
            return 0;

        memo = vector<vector<int>>(len + 1, vector<int>(aim + 1, 0));

        memo[len][0] = 1;

        for (int i = len - 1; i >= 0; i--)
        {
            for (int j = 0; j <= aim; j++)
            {
                /*for (int k = 0; j - k*arr[i] >= 0; k++)
                    memo[i][j] += memo[i + 1][j - k*arr[i]];
                */
                int n = (j - arr[i] >= 0) ? memo[i][j - arr[i]] : 0;
                memo[i][j] = memo[i + 1][j] + n;
            }
        }

        return memo[0][aim];
    }

private:
    vector<vector<int>> memo;       //memo[i][j]：从下标为[i...len-1]处选取任意张，可以换到j的方法数

};

2. 机器人走到指定位置的方法数

在一个长度为N的路上，下标为[1~N]。一个机器人初始在M位置，它可以走P步，如果在1位置则只能往右走，在N位置则只能往左走，请问机器人走P步后，停在K位置上的走法有多少种

暴力递归

int ways(int N, int M, int P, int K)
{
    if (N < 2 || M < 1 || M > N || P < 0 || K < 1 || K > N)
        return 0;

    if (P == 0)
        return (M == K) ? 1 : 0;

    int ret = 0;
    if (M == 1)
        ret = ways(N, M + 1, P - 1, K);
    else if (M == N)
        ret = ways(N, M - 1, P - 1, K);
    else
        ret = ways(N, M + 1, P - 1, K) + ways(N, M - 1, P - 1, K);

    return ret;
}

动态规划

memo[P][M] = memo[P-1][M-1] + memo[P-1][M+1]

int ways(int N, int M, int P, int K)
{
    if (N < 2 || M < 1 || M > N || P < 0 || K < 1 || K > N)
        return 0;

    vector<vector<int>> memo = vector<vector<int>>(P + 1, vector<int>(N + 1, 0));       //memo[i][j]：走了i步，到达j位置的方法数

    memo[0][K] = 1;

    for (int i = 1; i <= P; i++)
    {
        for (int j = 1; j <= N; j++)
        {
            memo[i][j] += (j - 1 < 1) ? 0 : memo[i - 1][j - 1];        //从左边一个位置往右走
            memo[i][j] += (j + 1 > N) ? 0 : memo[i - 1][j + 1];        //从右边一个位置往左走
        }
    }

    return memo[P][K];
}

更多动态规划例题