LeetCode典型题——动态规划

最新推荐文章于 2022-02-27 17:02:47 发布
最新推荐文章于 2022-02-27 17:02:47 发布
阅读量236 收藏
点赞数
CC 4.0 BY-SA版权
分类专栏： # 【02】刷题
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/zxt_1/article/details/90414939
本文探讨了LeetCode中涉及动态规划的典型题目，包括343, 62, 198, 213, 337和300等，解析了动态规划的解题思路，如状态转移方程，并提及了两种优化方法：优化1和优化2，旨在减少内存使用。" 132771506,19687618,使用Python与OpenCV在图像上叠加标签图,"['计算机视觉', '图像处理', 'Python编程', 'OpenCV库']

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

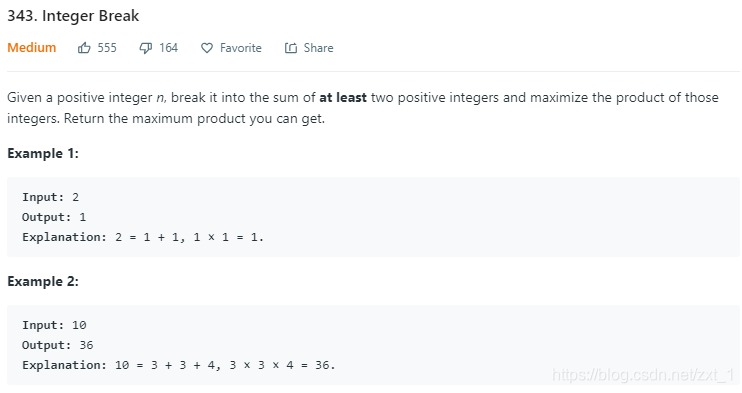
在这里插入图片描述
在这里插入图片描述

343

在这里插入图片描述
在这里插入图片描述

class Solution {
private:
    vector<int> memo;

    int breakInteger(int n){

        if(n == 1)
            return 1;

        if(memo[n] != -1)
            return memo[n];

        int res = -1;
        for(int i = 1 ; i < n ; i ++)
        {
            int tmp = max(i * (n - i) , i * breakInteger(n - i));	//别忘记  i*（n-i）
            res = max(res, tmp);
        }
           
        memo[n] = res;
        return res;
    }

public:
    int integerBreak(int n) {
       
        memo = vector<int>(n+1, -1);
        return breakInteger(n);
    }
};

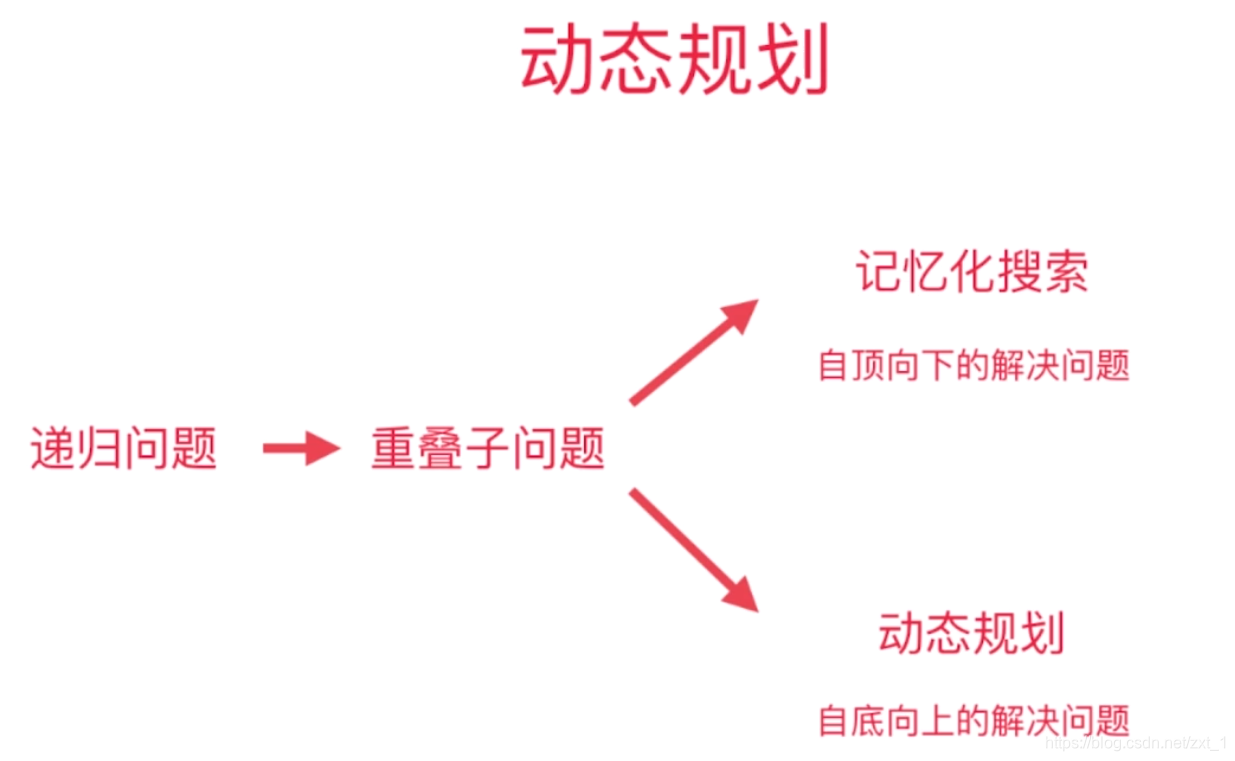
动态规划

class Solution {
private:
    vector<int> memo;


public:
    int integerBreak(int n) {
       
        memo = vector<int>(n+1, -1);
        
        memo[1] = 1;
        for(int i=2; i<=n; i++)
        {
            for(int j=1; j<=i-1; j++)
            {
                int tmp = max(j*(i-j), j*memo[i-j]);
                memo[i] = max(memo[i], tmp);
            }
        }
        
        return memo[n];
    }
};

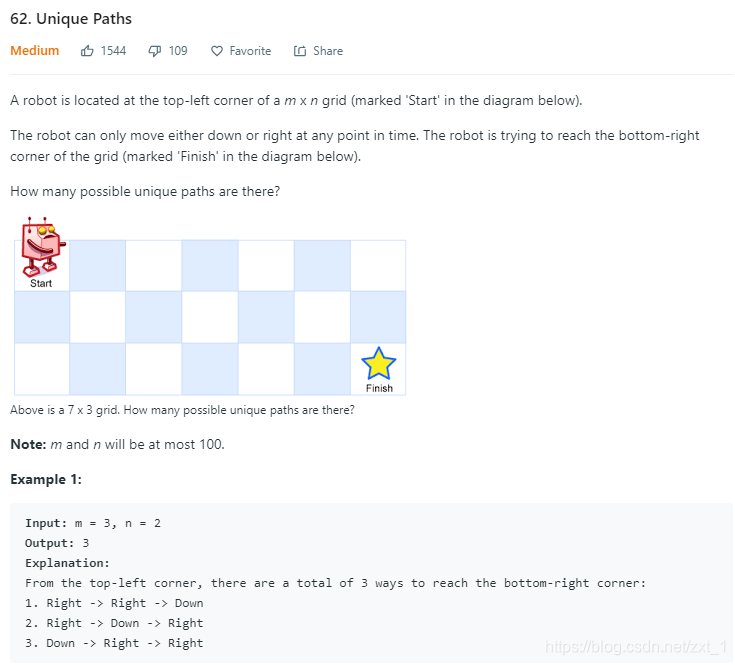
62

在这里插入图片描述

class Solution {
public:
    int uniquePaths(int m, int n) {
        
        memo = vector<vector<int>>(m, vector<int>(n, 1));       //memo[i][j] 保存到 节点[i][j] 的路径个数
                                                                //memo[i][j] = memo[i-1][j] + memo[i][j-1]
        for(int i=1; i<m; i++)
           for(int j=1; j<n; j++)
               memo[i][j] = memo[i-1][j] + memo[i][j-1];
        
        return memo[m-1][n-1];
        
    }
    
private:
    vector<vector<int>> memo;
};

198

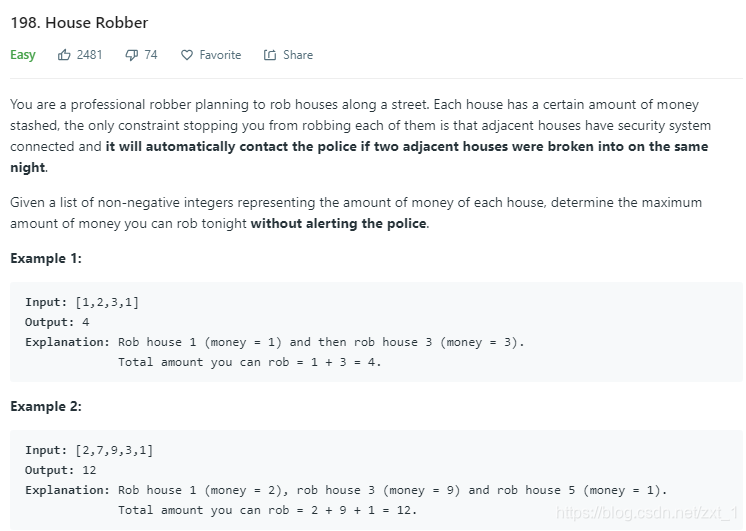
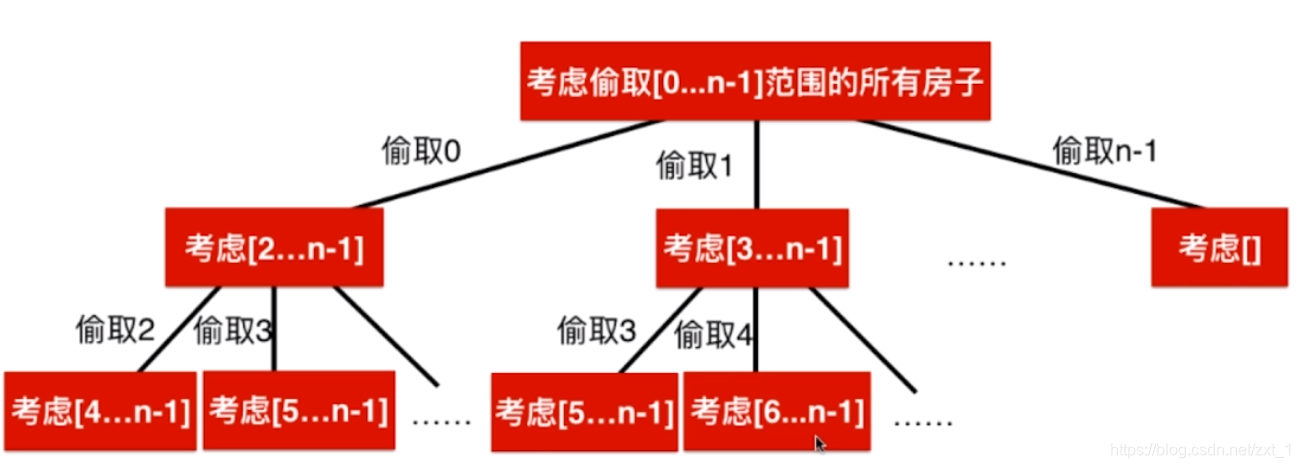
在这里插入图片描述
在这里插入图片描述

class Solution {
public:
    int rob(vector<int>& nums) {
        
        memo = vector<int>(nums.size(), -1);
        
        return help(nums, 0);
        
    }
    
private:
    vector<int> memo;
    
    int help(vector<int>& nums, int index)
    {
        if(index >= nums.size())
            return 0;
        
        if(memo[index] != -1)
            return memo[index];
        
        int ret = 0;
        for(int i=index; i<nums.size(); i++)
        {
            ret = max(nums[i]+help(nums, i+2), ret);
        }
        
        memo[index] = ret;
        return ret;
    }
};

动态规划

class Solution {
public:
    int rob(vector<int>& nums) {
        int n = nums.size();
        if( n == 0 )
            return 0;

        // the max profit for robbing nums[0...i]
        vector<int> memo(n, 0);
        memo[0] = nums[0];
        for(int i = 1 ; i < n ; i ++)
            memo[i] = max(memo[i - 1],
                          nums[i] + (i - 2 >= 0 ? memo[i - 2] : 0));

        return memo[n-1];
    }
    
private:
    vector<int> memo;    
};

213

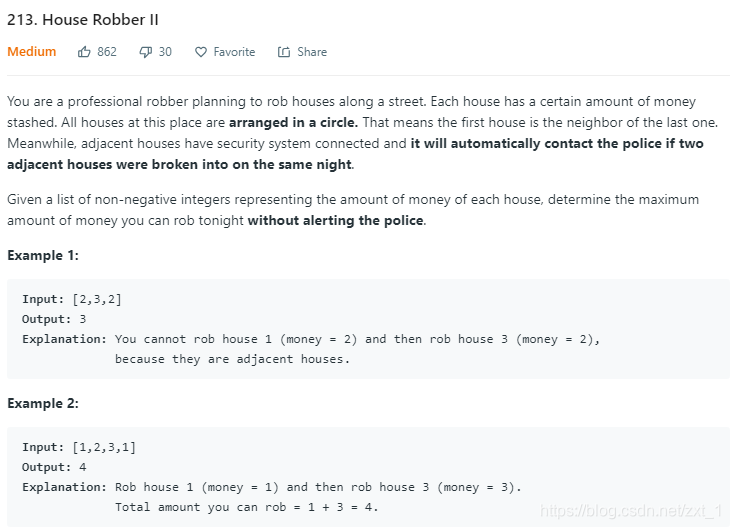
在这里插入图片描述

class Solution {
public:
    int rob(vector<int>& nums) {
        
        int n = nums.size();
        if( n == 0 )
            return 0;
        if(n == 1)
            return nums[0];

        // the max profit for robbing nums[0...i-1]
        vector<int> memo(n, 0);
        memo[0] = nums[0];
        for(int i = 1 ; i < n-1 ; i ++)
            memo[i] = max(memo[i - 1],
                          nums[i] + (i - 2 >= 0 ? memo[i - 2] : 0));

        // the max profit for robbing nums[1...i]
        vector<int> memo1(n, 0);
        memo1[0] = 0;
        for(int i = 1 ; i < n; i ++)
            memo1[i] = max(memo1[i - 1],
                          nums[i] + (i - 2 >= 0 ? memo1[i - 2] : 0));

        return max(memo[n-2], memo1[n-1]);
    }
    
private:
    vector<int> memo;
    vector<int> memo1;
    
};

337

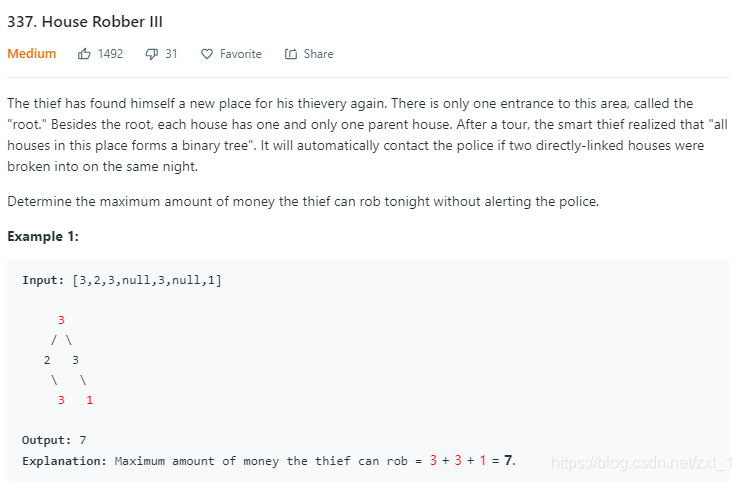
在这里插入图片描述

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int rob(TreeNode* root) {
        
        if(!root)
            return 0;
        
        int ret = help(root);
        return ret;
    }
    
private:
    unordered_map<TreeNode*, int> memo;
    
    int help(TreeNode *node)
    {
        if(!node)
            return 0;
        
        if(memo.find(node) != memo.end())
            return memo[node];
        
        int tmp = 0;
        if(node->left)
            tmp += help(node->left->left) + help(node->left->right);
        if(node->right)
            tmp += help(node->right->left) + help(node->right->right);
        
        tmp = max(node->val+tmp, help(node->left)+help(node->right));      //比较：当前节点+左、右节点的子树  左子树+右子树
        memo[node] = tmp;
        
        return tmp;
    }
};

300

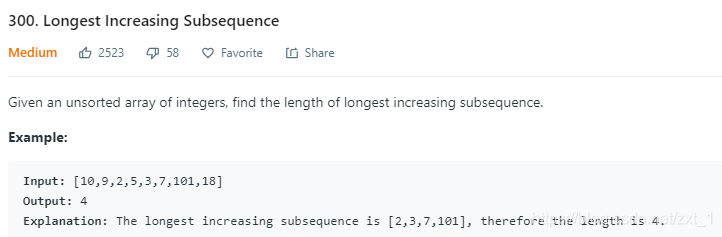
在这里插入图片描述

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        
        if(nums.size() == 0)
            return 0;
        
        memo = vector<int>(nums.size(), 1);     //memo[i]：以 nums[i] 为结尾的最长上升子序列的长度
        
        for(int i=1; i<nums.size(); i++)
            for(int j=0; j<i; j++)
            {
                if(nums[j] < nums[i])
                    memo[i] = max(memo[i], memo[j]+1);
            }
        
        sort(memo.begin(), memo.end());
        return memo[nums.size()-1];
    }
    
private:
    vector<int> memo;
};

动态规划

/**
 * Definition for an interval.
 * struct Interval {
 *     int start;
 *     int end;
 *     Interval() : start(0), end(0) {}
 *     Interval(int s, int e) : start(s), end(e) {}
 * };
 */

bool compare(const Interval& a, const Interval& b)
{
    if(a.start != b.start)
        return a.start < b.start;
    return a.end < b.end;
}

class Solution {
public:
    int eraseOverlapIntervals(vector<Interval>& intervals) 
    {
        
        if(intervals.size() == 0)
            return 0;
        
        sort(intervals.begin(), intervals.end(), compare);
        
        //memo[i] : intervals[0...i]所包含的最大不重叠区间个数
        memo = vector(intervals.size(), 1);
        
        for(int i=1; i<intervals.size(); i++)
            for(int j=0; j<i; j++)
            {
                if(intervals[j].end <= intervals[i].start)
                    memo[i] = max(memo[i], memo[j]+1);
            }
        
        sort(memo.begin(), memo.end());
        
        return intervals.size() - memo[intervals.size()-1];
    }
    
private:
    vector<int> memo;
};

贪心

bool compare(const Interval &a, const Interval &b){
    if(a.end != b.end)
        return a.end < b.end;
    return a.start < b.start;
}

/// 时间复杂度: O(n)
/// 空间复杂度: O(n)
class Solution {
public:
    int eraseOverlapIntervals(vector<Interval>& intervals) {

        if(intervals.size() == 0)
            return 0;

        sort(intervals.begin(), intervals.end(), compare);

        int res = 1;
        int pre = 0;
        for(int i = 1 ; i < intervals.size() ; i ++)
            if(intervals[i].start >= intervals[pre].end){
                res ++;
                pre = i;
            }

        return intervals.size() - res;
    }
};

在这里插入图片描述

F（i, c）:在i个物体中选择，背包容量为c，价值最大
F（i, c）= max（F(i-1，c)， v[i]+F(i-1，c-w[i])）

class Knapsack01{

private:
    vector<vector<int>> memo;

    // 选择 [0...index]的物品,填充容积为c的背包的最大价值
    int bestValue(const vector<int> &w, const vector<int> &v, int index, int c){

        if(c <= 0 || index < 0)
            return 0;

        if(memo[index][c] != -1)
            return memo[index][c];

        int res = bestValue(w, v, index-1, c);
        if(c >= w[index])
            res = max(res, v[index] + bestValue(w, v, index - 1, c - w[index]));
        memo[index][c] = res;
        return res;
    }

public:
    int knapsack01(const vector<int> &w, const vector<int> &v, int C){
        assert(w.size() == v.size() && C >= 0);
        int n = w.size();
        if(n == 0 || C == 0)
            return 0;

        memo = vector<vector<int>>(n, vector<int>(C+1, -1));
        return bestValue(w, v, n - 1, C);
    }
};

动态规划

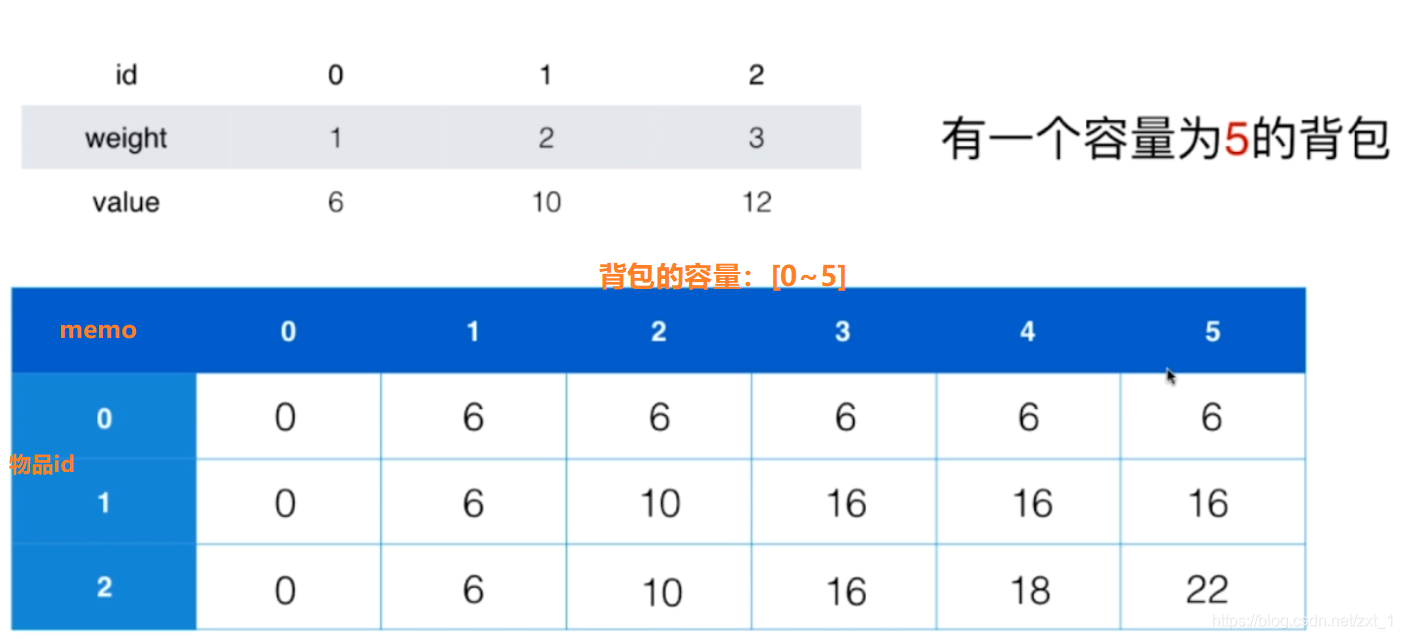
在这里插入图片描述

//时间复杂度: O(n * C) 其中n为物品个数; C为背包容积
//空间复杂度: O(n * C)

class Knapsack01{

public:
    int knapsack01(const vector<int> &w, const vector<int> &v, int C){
        assert(w.size() == v.size() && C >= 0);
        int n = w.size();
        if(n == 0 || C == 0)
            return 0;

        vector<vector<int>> memo(n, vector<int>(C + 1,0));

        for(int j = 0 ; j <= C ; j ++)
            memo[0][j] = (j >= w[0] ? v[0] : 0 );

        for(int i = 1 ; i < n ; i ++)
            for(int j = 0 ; j <= C ; j ++){
                memo[i][j] = memo[i-1][j];
                if(j >= w[i])
                    memo[i][j] = max(memo[i][j], v[i] + memo[i - 1][j - w[i]]);
            }
        return memo[n - 1][C];
    }
};

优化1:
在这里插入图片描述

/// 时间复杂度: O(n * C) 其中n为物品个数; C为背包容积
/// 空间复杂度: O(C), 实际使用了2*C的额外空间
class Knapsack01{

public:
    int knapsack01(const vector<int> &w, const vector<int> &v, int C){
        assert(w.size() == v.size() && C >= 0);
        int n = w.size();
        if( n == 0 && C == 0 )
            return 0;

        vector<vector<int>> memo(2, vector<int>(C + 1, 0));

        for(int j = 0 ; j <= C ; j ++)
            memo[0][j] = (j >= w[0] ? v[0] : 0);

        for(int i = 1 ; i < n ; i ++)
            for(int j = 0 ; j <= C ; j ++){
                memo[i % 2][j] = memo[(i-1) % 2][j];
                if(j >= w[i])
                    memo[i % 2][j] = max(memo[i % 2][j], v[i] + memo[(i-1) % 2][j - w[i]]);
            }
        return memo[(n-1) % 2][C];
    }
};

优化2:只使用一行大小为C的数组

/// 时间复杂度: O(n * C) 其中n为物品个数; C为背包容积
/// 空间复杂度: O(C), 只使用了C的额外空间
class Knapsack01{

public:
    int knapsack01(const vector<int> &w, const vector<int> &v, int C){
        assert(w.size() == v.size() && C >= 0);
        intn = w.size();
        if(n == 0 || C == 0)
            return 0;

        vector<int> memo(C+1,0);

        for(int j = 0 ; j <= C ; j ++)
            memo[j] = (j >= w[0] ? v[0] : 0);

        for(int i = 1 ; i < n ; i ++)
            for(int j = C ; j >= w[i] ; j --)
                memo[j] = max(memo[j], v[i] + memo[j - w[i]]);

        return memo[C];
    }
};

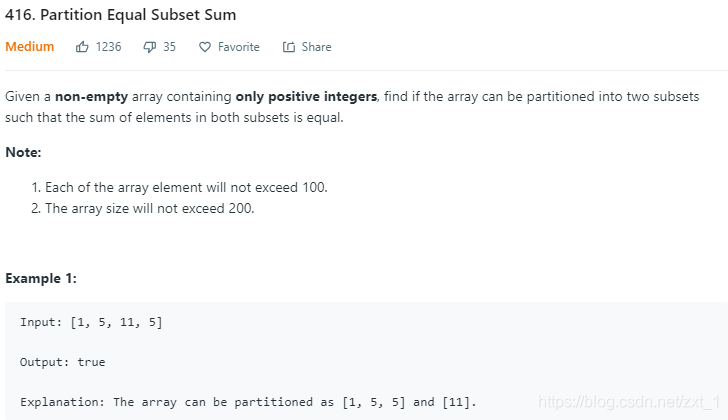
在这里插入图片描述
在这里插入图片描述

class Solution {
public:
    bool canPartition(vector<int>& nums) {
        
        int sum = 0;
        for(int i=0; i<nums.size(); i++)
            sum += nums[i];
        
        if(sum%2 != 0)
            return false;
        
        memo = vector<vector<int>>(nums.size(), vector<int>(sum/2+1, -1));
        
        return help(nums, nums.size()-1, sum/2);
    }
    
private:
    vector<vector<int>> memo;   //memo[i][c]    -1:没记录过 
                                //              0：nums[0...i]无法填满 大小为 C 的背包
                                //              1:nums[0...i] 可以填满 大小为 C 的背包
    
    bool help(vector<int> &nums, int index, int C)      //  nums[0...index] 能否填满 大小为 C 的背包
    {
        if(C == 0)
            return true;
        
        if(index < 0 || C < 0)
            return false;
        
        if(memo[index][C] != -1)
            return (memo[index][C] == 0)?false:true;
        
        memo[index][C] = help(nums, index-1, C) || help(nums, index-1, C-nums[index]);
        
        return memo[index][C];
    }
};

在这里插入图片描述
在这里插入图片描述

Soul 算法笔试题——火柴拼接数字——动态规划问题
weixin_46214235的博客
09-28 1012
笔者最近一直在刷动态规划方面算法，昨天 Soul 笔试算法题遇到了一个经典动态规划问题，在此做个记录。 题目：用火柴拼接数字，数字 1-9 所需火柴数量分别为：2，5，5，4，5，6，3，7，6，现在给定一个数字，表示总共火柴数量 n，给定一个数组 arr,表示只能组合出该数字。如：n = 5, arr = [1, 3, 6]，则表示，用5根火柴将1 ，3，6 中的某些数字进行组合，每一个数字可以被多次使用，得到最终结果。写一个方法，返回值为在 n 根火柴的条件下，arr 数组中，能被拼接出的最大值为多少.
leetcode 2024春招冲刺百题计划——动态规划+数论
最新发布
m0_63289912的博客
03-29 1839
不打算充钱第一次用java写，有点不熟悉。。。还是用c+stl爽。没写完，不定期更新。会尽快的，先发出来吧，万一有人需要呢先更数论和动态规划。
Leetcode-动态规划典型题
JINGYUSHAN的博客
02-10 685
LC053.Maximum Subarray最大子数组和 一、题目 给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。 子数组 是数组中的一个连续部分。 示例 1： 输入：nums = [-2,1,-3,4,-1,2,1,-5,4] 输出：6 解释：连续子数组[4,-1,2,1] 的和最大，为6 。 示例 2： 输入：nums = [1] 输出：1 示例 3： 输入：nums = [5,4,-1,7,8] 输出：23 提示...
笔试编程题必杀技——动态规划
yearningseeker的博客
05-06 1168
在笔试编程题中，最常见题型莫过于动态规划了，以前一直不太清楚，今天下定决心好好梳理一番。 动态规划是通过组合子问题的解决而解决整个问题的，一个大问题分解成一个小问题，这个小问题再分成小问题，以此类推，直至求出最终结果。 首先看一个把我虐了无数遍的问题：最大子数组的问题。 题目：一个有N个整数元素的一位数组(A[0], A[1],...,A[n-1], A[n])，这个数组当然有很多子数组，那
P1966 火柴排队————洛谷 动态规划
qq_39910498的博客
12-17 240
P1966 火柴排队 这一题可以看成是逆序对问题的应用（逆序对问题） 首先，我们可以知道当所有高度最小的时候，有两个序列中第k大的元素刚好配对，这里就不给出证明了。 然后呢，我们通过对下标（将下标所对应的值作为关键字）的排序，再分别将两个数组的下标匹配，，其中的逆序对个数极为所求的最小的移动次数。 #include<stdio.h> #include<stdlib.h> #define size 500005 int mod = 1e8 - 3; int tmp[size], a
动态规划_方法总结
BeiYu
11-03 1023
动态规划方法总结 1. 按状态类型分 写在前面： 从状态类型分，并不表示一题只从属于一类。其实一类只是一种状态的表示方法。可以好几种方法组合成一个状态，来解决问题。 1.1.编号（长度）动态规划共性总结： 本类的状态是基础的基础，大部分的动态规划都要用到它，成为一个维。一般来说，有两种编号的状态： 1、状态(i)表示前i 个元素决策组成的一个状态。
C语言实现leetcode0322题——零钱兑换解法
这是一个典型的求最小值问题，可以使用动态规划算法求解。首先分析问题，确定状态表达式以及状态转移方程。 知识点三：状态定义与初始化 在动态规划算法中，定义状态是解决问题的关键一步。对于“0322. Coin Change...
LeetCode刷题笔记——#70. 爬楼梯
12-22
所以这是一个典型的斐波那契数列。   一般做斐波那契数列我们会用递归的方式，然而不知道为什么，这道题用递归会超时，所以还是稳着点写。 ###### leetcode 代码主体 ###### class Solution: def climbStairs...
Leetcode典型题解答和分析、归纳和汇总——T56（合并区间）
01-06
本题考察简单的数据排序知识点。 class Solution{ public: vector<vector> merge(vector<vector>& intervals){ vector<vector> res; //作为返回结果 if(intervals.empty()) return res; sort(intervals.begin...
Leetcode典型题解答和分析、归纳和汇总——T40（组合总和II）
01-06
本题与T39具有异曲同工之妙，都可以采用回溯算法来进行求解。该题有两个需要注意的点 【1】数组元素不能出现重复的数字【2】不能出现重复的组合 首先我们把这个数组进行排序（升序），数组中的每个数字在每个组合中...
动态规划经典题目及答案
01-25
关于动态规划的一些经典题目，有助于提高编程能力，对于学习有很大的准备，，！！！期待大家学习分享！
动态规划：游戏赢家（一）
Peanut 大本营
04-19 779
    给定一个非负数组，A、B两人玩游戏，轮流从数组的头部或者尾部取出元素，加到各自的和中，直到数组元素取完，取到的元素和最大的玩家赢。问对于给定的数组，先开始的玩家能否保证赢得游戏（如果相等也算先手的玩家赢）。    例如给定数组为[1, 5, 233, 7]，A为开始第一步的玩家。A可以取1或者7，如果A先取1，剩下[5, 233, 7]；B可以取5或者7，但不管B取任何元素，A都可以取23...
Leetcode第一题：两数之和（3种语言）
热门推荐
三年研究生能改变多少
12-08 4万+
@](这里写自定义目录标题) Leetcode第一题：两数之和 给定一个整数数组 nums 和一个目标值 target，请你在该数组中找出和为目标值的 两个 整数。 你可以假设每种输入只会对应一个答案。但是，你不能重复利用这个数组中同样的元素。 示例: 给定 nums = [2, 7, 11, 15], target = 9 因为 nums[0] + nums1 = 2 + 7 = 9 所以返回 ...
leetcode回溯专题
John的博客
04-09 176
22.括号生成 class Solution { public: vector<string> res; vector<string> generateParenthesis(int n) { if (n == 0) return {}; string track; //可用的...
LeetCode 解题笔记（二）数组篇
火山上的企鹅
02-27 8910
文章目录26.删除排序数组中的重复--2022/01/16122. 买卖股票的最佳时机 II--2022/01/17189. 轮转数组--2022/01/18217. 存在重复元素--2022/01/19136. 只出现一次的数字--2021/12/14350. 两个数组的交集 II -- 2022/01/1266. 加一 -- 2022/01/201.两数之和 系列篇:      Qt TCP/UDP 网络协议入门实操（一）TCP通讯 Qt TCP/UDP
编程训练第五十期——合并区间
yudi4789的博客
03-18 635
编程题目： 以数组 intervals 表示若干个区间的集合，其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间，并返回一个不重叠的区间数组，该数组需恰好覆盖输入中的所有区间。 示例： 输入：intervals = [[1,3],[2,6],[8,10],[15,18]] 输出：[[1,6],[8,10],[15,18]] 解释：区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6]. 输入：intervals = [[1,4],[4,5]]
【总结】动态规划类型
火柴的初心的博客
07-01 739
1.按摩师（leetcode 面试题17.16） 日期：2020/3/24 题目描述： 一个有名的按摩师会收到源源不断的预约请求，每个预约都可以选择接或不接。在每次预约服务之间要有休息时间，因此她不能接受相邻的预约。给定一个预约请求序列，替按摩师找到最优的预约集合（总预约时间最长），返回总的分钟数。 注意：本题相对原题稍作改动 示例 1： 输入： [1,2,3,1] 输出： 4 解释：...
面试经典动态规划，n个相同火柴分堆
u011048943的博客
04-13 1302
题目描述： 现在有n个相同火柴，将这些火柴分成若干堆，问所有的分法总数。 题目分析： 初见题目第一反应是采用组合数学的方法来计算，有种叫Stirling数的组合数。他表示将n个不同物品分到k堆里，注意这里是n个不同物品，所以不能采用stirling数。 那么我们简单的做几个尝试好了，假设n=4,那么可以分如下几种： 4 1,3 和 3,1算一种 2,2  1,1,2 和 1,2
leetcode中一些经典动态规划题（不定期更新）
MaloFleur
07-19 2473
115. Distinct Subsequences 状态转移方程： dp[i][j]={dp[i][j−1],s[j]!=t[i]dp[i][j−1]+dp[i−1][j−1],s[j]==t[i] dp[i][j]=\begin{cases} dp[i][j - 1],\qquad\qquad\qquad\qquad\quad s[j] !=t[i] \\\\ dp[i][j - 1] + ...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值