以下内容为对Datawhale2021年11月组队学习中“水很深的深度学习”课程的卷积神经网络的简要总结。
原文链接: https://datawhalechina.github.io/unusual-deep-learning/
卷积神经网络CNN
CNN的引出:全连接神经网络的权重矩阵的参数非常多,而且往往自然图像中的物体都具有局部不变性特征,即尺度缩放、平移、旋转等操作不影响其语义信息,但是全连接前馈网络很难提取这些局部不变特征,这就引出了我们将要介绍的卷积神经网络
卷积神经网络也是一种前馈神经网络,是受到生物学上感受野(感受野主要是指听觉系统、本体感觉系统和视觉系统中神经元的一些性质)的机制而提出的(在视觉神经系统中,一个神经元的感受野是指视网膜上的特定区域,只有这个区域内的刺激才能够激活该神经元)。
卷积
(f∗g)(n)(f*g)(n)(f∗g)(n)成为 f 和 g 的卷积,连续卷积和离散卷积可以表达为如下形式:
- 连续卷积:(f∗g)(n)=∫−∞∞f(τ)g(n−τ)dτ(f*g)(n)=\int_{-∞}^{∞}f(τ)g(n−τ)dτ(f∗g)(n)=∫−∞∞f(τ)g(n−τ)dτ
n=τ+(n−τ)n=τ+(n−τ)n=τ+(n−τ) - 离散卷积:(f∗g)(n)=∑−∞∞f(τ)g(n−τ)dτ(f*g)(n)=\sum_{-∞}^{∞}f(τ)g(n−τ)dτ(f∗g)(n)=∑−∞∞f(τ)g(n−τ)dτ
卷积的应用
卷积有很多应用,经常用于处理一个输入,通过系统产生一个适应需求的输出。

- 统计学中加权平均法
- 概率论中两个独立变量之和概率密度的计算
- 信号处理中的线性系统
- 物理学的线性系统
- 图像处理中的应用(卷积神经网络)
卷积经常用在信号处理中,用于计算信号的延迟累积。
例:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-n2nKzv2n-1637814291044)(./]86_KH1`HXHEIYVI3SY.png)]](https://i-blog.csdnimg.cn/blog_migrate/abc539e2d251b9626dddd07341b8cdcf.png)
不同的滤波器来提取信号序列中的不同特征:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-TBW5yAeg-1637814291045)(./1637641809814.png)]](https://i-blog.csdnimg.cn/blog_migrate/f24573fdb5790b32821cf307cc6d3b9e.png)
引入滤波器的滑动步长S和零填充P:
- 步长( Stride):指卷积核在滑动时的时间间隔。
- 零填充( Zero Padding):在输入向量两端进行补零。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-4gvi9LPP-1637814291047)(./1637642011236.png)]](https://i-blog.csdnimg.cn/blog_migrate/b9258060ed55ea40be331b73e6d6da13.png)
卷积的结果按输出长度不同可以分为三类:
- 窄卷积:步长 𝑇 = 1 ,两端不补零 𝑃 = 0 ,卷积后输出长度为 𝑀 − 𝐾 + 1
- 宽卷积:步长 𝑇 = 1 ,两端补零 𝑃 = 𝐾 − 1 ,卷积后输出长度 𝑀 + 𝐾 − 1
- 等宽卷积:步长 𝑇 = 1 ,两端补零 𝑃 =(𝐾 − 1)/2 ,卷积后输出长度 𝑀
早期文献的卷积默认为窄卷积,目前文献中一般默认为等宽卷积
在图像处理中,图像是以二维矩阵的形式输入到神经网络中,因此需要二维卷积。
二维卷积定义:
一个输入信息 XXX和滤波器 WWW 的二维卷积为:
Y=W∗XY=W∗XY=W∗X即:
∑u=1U∑v=1Vwuvxi−u+1,j−v+1\sum_{u=1}^{U}\sum_{v=1}Vw_{uv}x_{i-u+1,j-v+1}u=1∑Uv=1∑Vwuvxi−u+1,j−v+1
示例:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-tKN7itBD-1637814291048)(./1637663251914.png)]](https://i-blog.csdnimg.cn/blog_migrate/445c9c557c3902957a806866cd2bf2d0.png)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-JHfQeL1v-1637814291049)(./1637663257383.png)]](https://i-blog.csdnimg.cn/blog_migrate/145f577b31c66bd8bd40cd8ddab40141.png)
卷积层映射关系:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-xNsgvcrm-1637814291050)(./1637663727293.png)]](https://i-blog.csdnimg.cn/blog_migrate/2141ac8bab42f4a208feba47ed20b7ac.png)
多个卷积核的情况:下图是表示步长2、filter 3*3 、filter个数6、零填充 1的情形。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-LMby8TNr-1637814291052)(./1637667158418.png)]](https://i-blog.csdnimg.cn/blog_migrate/002707073ff733c4fb627eba0ae5d308.png)
特征图的计算:
典型的卷积层为3维结构
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Skuyold8-1637814291053)(./1637668482514.png)]](https://i-blog.csdnimg.cn/blog_migrate/72b5d9094513642a7f07f1d5cc422c7c.png)
转置卷积/微步卷积:低维特征映射到高维特征
-
转置卷积
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-dr6Q1cj3-1637814291055)(./FSZO_CN5IVPW[X`O8@WFR.png)]](https://i-blog.csdnimg.cn/blog_migrate/4fa03a3d7a637da46593ee067ef17452.png)
-
微步卷积
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-sgKucTmw-1637814291056)(./TT45H{$2P4@0LV]XMHO`20D.png)]](https://i-blog.csdnimg.cn/blog_migrate/8308073dfd10444ed6070926015ae88c.png)
-
空洞卷积:为了增加输出单元的感受野,通过给卷积核插入“空洞”来变相地增加其大小。
![- [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-W7rIdG3I-1637814291056)(./1637670230355.png)]](https://i-blog.csdnimg.cn/blog_migrate/dfd65a1df4b5da2eeab62acb299481c6.png)
卷积神经网络基本原理
卷积神经网络的基本结构大致包括:卷积层、激活函数、池化层、全连接层、输出层等。
卷积层:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-mYHO4Nzb-1637814291057)(./]4W[V1ON{5R_FXT$]JUQKRI.png)]](https://i-blog.csdnimg.cn/blog_migrate/8e52f6898ab089f853550b0c97ad0cc3.png)
卷积实际上就是互相关
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-sRj8QixY-1637814291058)(./1637671831082.png)]](https://i-blog.csdnimg.cn/blog_migrate/bb6c3676b2f6d2524cebe2bfe01820f0.png)
卷积的步长:卷积核移动的步长
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-vcGBKnPW-1637814291059)(./1637671951746.png)]](https://i-blog.csdnimg.cn/blog_migrate/fc06316f03d84aab3291dbf79e8cee4c.png)
卷积的模式:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-SMtOTznl-1637814291060)(./1637672837784.png)]](https://i-blog.csdnimg.cn/blog_migrate/12557a18d21b8e33850d911bbea4b357.png)
- Full:从filter和image刚相交开始做卷积,白色部分为填充0。
- same:当filter的中心(K)与image的边角重合时,开始做卷积运算。此外,same还有一个含义便是卷积之后输出的feature map尺寸相对于输入图片保持不变。
- valid:当filter全部在image里面的时候,进行卷积运算。
数据填充:如果我们有一个 𝑛×𝑛 的图像,使用𝑓×𝑓 的卷积核进行卷积操作,在进行卷积操作之前我们在图像周围填充 𝑝 层数据,输出的维度:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-QqHkc5ev-1637814291061)(./1637673281538.png)]](https://i-blog.csdnimg.cn/blog_migrate/2cdcb0005c9d40d2152180d42c9ed57b.png)
感受野:卷积神经网络每一层输出的特征图(featuremap)上的像素点在输入图片上映射的区域大小,即特征图上的一个点对应输入图上的区域。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-7IVoEDjS-1637814291062)(./1637673748718.png)]](https://i-blog.csdnimg.cn/blog_migrate/cee8a65c4fe4dea708372b6fff5f086c.png)
可以采用从后往前逐层的计算方法计算感受野的大小:
- 第 i 层的感受野大小和第 i-1 层的卷积核大小和步长有关系,同时也与第 (i-1)层感受野大小有关。
- 假设最后一层(卷积层或池化层)输出特征图感受野的大小(相对于其直接输入而言)等于卷积核的大小。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-X0A8RHgj-1637814291064)(./1637718941185.png)]](https://i-blog.csdnimg.cn/blog_migrate/fcd796f88ef0601677feeac3de97bbba.png)
卷积层的深度(卷积核个数):一个卷积层通常包含多个尺寸一致的卷积核
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-E6o1bTxe-1637814291064)(./1637719725793.png)]](https://i-blog.csdnimg.cn/blog_migrate/17a8084589a99ccc125b4a660e1d8938.png)
激活函数
激活函数是用来加入非线性因素,提高网络表达能力,卷积神经网络中最常用的是ReLU,Sigmoid使用较少。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-WHVLfLgi-1637814291065)(./1637722149965.png)]](https://i-blog.csdnimg.cn/blog_migrate/15c740734c1050983bef2dda0e256b10.png)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-rQHtOWHY-1637814291066)(./1637722153958.png)]](https://i-blog.csdnimg.cn/blog_migrate/ff880f96c0885053591a74074ea98166.png)
ReLU函数
D(x)={0,x<0x,x≥0D(x) = \begin{cases} 0,&x<0 \\ x,&x≥0 \\ \end{cases}D(x)={0,x,x<0x≥0
ReLU函数的优点:
- 计算速度快,ReLU函数只有线性关系,比Sigmoid和Tanh要快很多
- 输入为正数的时候,不存在梯度消失问题
ReLU函数的缺点:
- 强制性把负值置为0,可能丢掉一些特征
- 当输入为负数时,权重无法更新,导致“神经元死亡”(学习率不要太大)
为什么会导致神经元死亡:
对于正例y=WTX+by=W^{T}X+by=WTX+b,y_要变大,则更新权重W,使得W变大,负例y_要变小,更新权重W使得W变小,如果学习率设置较大,在遇到负例的时候,W会突然变的很小,会导致所有样本在某一结点处,全部输出为负数,这时,梯度无法经 ReLU 反向传播至 ReLU 的输入函数。也就是说,这个神经元的参数再也不会更新了,即神经元死亡。
Parametric ReLU
D(x)={αx,x<0x,x≥0D(x) = \begin{cases} αx,&x<0 \\ x,&x≥0 \\ \end{cases}D(x)={αx,x,x<0x≥0
-
当 𝛼=0.01 时,称作Leaky ReLU
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-nrhGjQzt-1637814291066)(./]$W0_A}N}MJDZFIUVJDBR.png)]](https://i-blog.csdnimg.cn/blog_migrate/9e7d979865e4cc8e701163b3134206ff.png)
-
当 𝛼 从高斯分布中随机产生时,称为Randomized ReLU(RReLU)
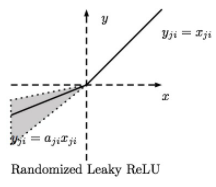
PReLU函数的优点:
- 比sigmoid/tanh收敛快
- 解决了ReLU的“神经元死亡”问题
PReLU函数的缺点:需要再学习一个参数,工作量变大
ELU函数
D(x)={α(ex−1),x<0x,x≥0D(x) = \begin{cases} α(e^{x}-1),&x<0 \\ x,&x≥0 \\ \end{cases}D(x)={α(ex−1),x,x<0x≥0
ELU函数的优点:
- 处理含有噪声的数据有优势
- 更容易收敛
ELU函数的缺点:计算量较大,收敛速度较慢
对于激活函数的选取:
- CNN在卷积层尽量不要使用Sigmoid和Tanh,将导致梯度消失。
- 首先选用ReLU,使用较小的学习率,以免造成神经元死亡的情况。
- 如果ReLU失效,考虑使用Leaky ReLU、PReLU、ELU或者Maxout,此时一般情况都可以解决
特征图
- 浅层卷积层:提取的是图像基本特征,如边缘、方向和纹理等特征
- 深层卷积层:提取的是图像高阶特征,出现了高层语义模式,如“车轮”、“人脸”等特征
池化层
池化操作使用某位置相邻输出的总体统计特征作为该位置的输出,常用最大池化(max-pooling)和均值池化(average- pooling)。
池化层不包含需要训练学习的参数,仅需指定池化操作的核大小、操作步幅以及池化类型。
池化的作用:
- 减少网络中的参数计算量,从而遏制过拟合
- 增强网络对输入图像中的小变形、扭曲、平移的鲁棒性(输入里的微小扭曲不会改变池化输出——因为我们在局部邻域已经取了最大值/ 平均值)
- 帮助我们获得不因尺寸而改变的等效图片表征。这非常有用,因为 这样我们就可以探测到图片里的物体,不管它在哪个位置
全连接层
- 对卷积层和池化层输出的特征图(二维)进行降维
- 将学到的特征表示映射到样本标记空间的作用
输出层
- 分类问题,使用Softmax函数 yi=ezi∑i=1neziy_{i}=\frac{e^{z_{i}}}{\sum_{i=1}^{n}e^{z_{i}}}yi=∑i=1neziezi
- 回归问题, 使用线性函数 yi=∑m=1Mwimxmy_{i}=\sum_{m=1}^{M}w_{im}x_{m}yi=∑m=1Mwimxm
卷积神经网络的训练
- 1.用随机数初始化所有的卷积核和参数/权重
- 2.将训练图片作为输入,执行前向步骤(卷积, ReLU,池化以及全连接层的前向传播)并计算每个类别的对应输出概率。
- 3.计算输出层的总误差
- 4.反向传播算法计算误差相对于所有权重的梯度,并用梯度下降法更新所有的卷积核和参数/权重的值,以使输出误差最小化
卷积核个数、卷积核尺寸、网络架构这些参数,是在第一步之前就已经固定的,且不会在训练过程中改变——只有卷 积核矩阵和神经元权重会更新。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-HteA6gJi-1637814291068)(./1637747995699.png)]](https://i-blog.csdnimg.cn/blog_migrate/13fdd4c0c3fd477d657a1b2cec762b40.png)
和多层神经网络一样,卷积神经网络中的参数训练也是使用误差反向传播算法,关于池化层的训练则是将池化层改为多层神经网络的形式。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-VxEqiNCP-1637814291068)(./1637749236516.png)]](https://i-blog.csdnimg.cn/blog_migrate/cf6ee4305ee896959c09709c28f5f587.png)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-bTTIrZb7-1637814291069)(./1637749358026.png)]](https://i-blog.csdnimg.cn/blog_migrate/93c456da1369939829e0af8c33610286.png)
将卷积层也改为多层神经网络的形式:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-aCQ6P3jh-1637814291069)(./1637749377536.png)]](https://i-blog.csdnimg.cn/blog_migrate/5256bb42672863386fb56ff160e4553b.png)
经典卷积神经网络
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-piRUXEPP-1637814291070)(./1637749786735.png)]](https://i-blog.csdnimg.cn/blog_migrate/b95f6e73095d7996f6789cf6a9a3401a.png)
1. LeNet-5
LeNet-5由LeCun等人于1998年提出,主要进行手写数字识别和英文字母识别。是很经典的卷积神经网络,是学习卷积神经网络的基础。
网络结构
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-SRIDVPJ2-1637814291070)(./1637750005706.png)]](https://i-blog.csdnimg.cn/blog_migrate/be95ad6a9e06e0353cfac36f0ccc02fe.png)
- 输入层:32∗3232∗3232∗32 的图片,也就是相当于1024个神经元
- C1层(卷积层):选择6个 5∗55∗55∗5 的卷积核,得到6个大小为32−5+1=2832-5+1=2832−5+1=28的特征图,也就是神经元的个数为 6∗28∗28=47046∗28∗28=47046∗28∗28=4704
- S2层(下采样层):每个下抽样节点的4个输入节点求和后取平均(平均池化),均值乘上一个权重参数加上一个偏置参数作为激活函数的输入,激活函数的输出即是下一层节点的值。池化核大小选择2∗22∗22∗2,得到6个14∗1414∗1414∗14 大小特征图.
- C3层(卷积层):用5∗55∗55∗5的卷积核对S2层输出的特征图进行卷积后,得到6张10∗1010∗1010∗10 新图片,然后将这6张图片相加在一起,然后加一个偏置项b,然后用激活函数进行映射,就可以得到1张10∗1010∗1010∗10的特征图。我们希望得到 16 张10∗1010∗1010∗10的特征图 , 因此我们就需要参数个数为16∗(6∗(5∗5))=16∗6∗(5∗5)16∗(6∗(5∗5))=16∗6∗(5∗5)16∗(6∗(5∗5))=16∗6∗(5∗5)个参数.
- S4层(下采样层):对C3的16张10∗1010∗1010∗10特征图进行最大池化,池化核大小为2∗22∗22∗2,得到16张大小为5∗55∗55∗5的特征图。神经元个数已经减少为:16∗5∗5=40016∗5∗5=40016∗5∗5=400.
- C5层(卷积层):用5∗55∗55∗5的卷积核进行卷积,然后我们希望得到120个特征图,特征图大小为5−5+1=15-5+1=15−5+1=1。神经元个数为120(这里实际上是全连接,但是原文还是称之为了卷积层).
- F6层(全连接层):有84个节点,该层的训练参数和连接数都(120+1)∗84=10164(120+1)∗84=10164(120+1)∗84=10164.
- Output层:共有10个节点,分别代表数字0到9,如果节点i的输出值为0,则网络识别的结果是数字i。采用的是径向基函数(RBF)的网络连接方式:
yi=∑j(x−j−wij)2 y_{i}= \sum_{j}(x-j-w_{ij})^{2}yi=j∑(x−j−wij)2
总结:卷积核大小、卷积核个数(特征图需要多少个)、池化核大小(采样率多少)这些参数都是变化的,这就是所谓的CNN调参,需要学会根据需要进行不同的选择。
2. AlexNet
AlexNet由Hinton的学生Alex Krizhevsky于2012年提出,获得ImageNet LSVRC-2012(物体识别挑战赛)的冠军,1000个类别120万幅高清图像(Error: 26.2%(2011) →15.3%(2012)),通过AlexNet确定了CNN在计算机视觉领域的王者地位。
- 首次成功应用ReLU作为CNN的激活函数
- 使用Dropout丢弃部分神元,避免了过拟合
- 使用重叠MaxPooling(让池化层的步长小于池化核的大小), 一定程度上提升了特征的丰富性
- 使用CUDA加速训练过程
- 进行数据增强,原始图像大小为256×256的原始图像中重复截取224×224大小的区域,大幅增加了数据量,大大减 轻了过拟合,提升了模型的泛化能力
网络结构:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-bGhv3D9u-1637814291071)(./1637761189023.png)]](https://i-blog.csdnimg.cn/blog_migrate/1f031fb7d79f6752665b730c466b6dbe.png)
AlexNet可分为8层(池化层未单独算作一层),包括5个卷 积层以及3个全连接层
输入层:AlexNet首先使用大小为224×224×3图像作为输入(后改为227×227×3)
第一层(卷积层):包含96个大小为11×11的卷积核,卷积步长为4,因此第一层输出大小为55×55×96;然后构建一个核大小为3×3、步长为2的最大池化层进行数据降采样,进而输出大小为27×27×96
第二层(卷积层):包含256个大小为5×5卷积核,卷积步长为1,同时利用padding保证 输出尺寸不变,因此该层输出大小为27×27×256;然后再次通过 核大小为3×3、步长为2的最大池化层进行数据降采样,进而输出大小为13×13×256
第三层与第四层(卷积层):均为卷积核大小为3×3、步长为1的same卷积,共包含384个卷积核,因此两层的输出大小为13×13×384
第五层(卷积层):同样为卷积核大小为3×3、步长为1的same卷积,但包含256个卷积 核,进而输出大小为13×13×256;在数据进入全连接层之前再次 通过一个核大小为3×3、步长为2的最大池化层进行数据降采样, 数据大小降为6×6×256,并将数据扁平化处理展开为9216个单元
第六层、第七层和第八层(全连接层):全连接加上Softmax分类器输出1000类的分类结果,有将近6千万个参数
3. VGGNet
VGGNet由牛津大学和DeepMind公司提出
相较于AlexNet,VGG-16(比较常用,结构规整,具有很强的拓展性)网络模型中的卷积层均使用3∗33∗33∗3的卷积核,且均为步长为1的same卷积,池化层均使用 2∗22∗22∗2的池化核,步长为2
网络结构
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-dZzOtZdN-1637814291072)(./1637804073677.png)]](https://i-blog.csdnimg.cn/blog_migrate/acb2f81123645acf5a680ee9897fcbaa.png)
- 两个卷积核大小为3∗33∗33∗3的卷积层串联后的感受野尺寸为5∗55∗55∗5, 相当于单个卷积核大小为5∗55∗55∗5的卷积层
- 两者参数数量比值为$(2∗3∗3)/(5∗5)=72% $,前者参数量更少
- 此外,两个的卷积层串联可使用两次ReLU激活函数,而一个卷积层只使用一次
4. Inception Net
Inception Net 是Google公司2014年提出,获得ImageNet LSVRC-2014冠军。文章提出获得高质量模型最保险的做法就是增加模型的深度(层数)或者是其宽度(层核或者神经元数),采用了22层网络。
- 深度:层数更深,采用了22层,在不同深度处增加了两个 loss来避免上述提到的梯度消失问题
- 宽度:Inception Module包含4个分支,在卷积核3x3、5x5 之前、max pooling之后分别加上了1x1的卷积核,起到了降低特征图厚度的作用(1×1的卷积的作用:可以跨通道组织信息,来提高网络的表达能力;可以对输出通道进行升维和降维。)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-mUOy0LTj-1637814291072)(./1637804398314.png)]](https://i-blog.csdnimg.cn/blog_migrate/f05d7af5f42e2830749a029a2f2efcba.png)
5. ResNet
ResNet(Residual Neural Network),又叫做残差神经网络,是由微软研究院的何凯明等人2015年提出,获得ImageNet ILSVRC 2015比赛冠军,获得CVPR2016最佳论文奖。
随着卷积网络层数的增加,误差的逆传播过程中存在的梯 度消失和梯度爆炸问题同样也会导致模型的训练难以进行,甚至会出现随着网络深度的加深,模型在训练集上的训练误差会出现先降低再升高的现象。残差网络的引入则有助于解决梯度消失和梯度爆炸问题。
残差块
ResNet的核心是叫做残差块(Residual block)的小单元, 残差块可以视作在标准神经网络基础上加入了跳跃连接(Skip connection).
- 原连接
al+1=σ(Wl+1al+bl+1)a_{l+1}=σ(W_{l+1}a_{l}+b_{l+1})al+1=σ(Wl+1al+bl+1)
al+2=σ(Wl+2al+1+bl+2)a_{l+2}=σ(W_{l+2}a_{l+1}+b_{l+2})al+2=σ(Wl+2al+1+bl+2)
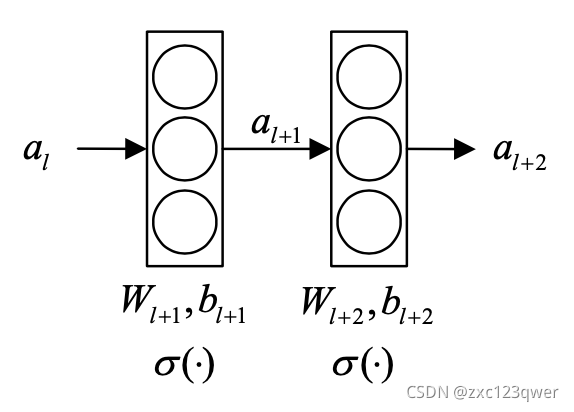
- 跳跃连接
al+1=σ(Wl+1al+bl+1)a_{l+1}=σ(W_{l+1}a_{l}+b_{l+1})al+1=σ(Wl+1al+bl+1)
al+2=σ(Wl+2al+1+bl+2+al)a_{l+2}=σ(W_{l+2}a_{l+1}+b_{l+2}+a_{l})al+2=σ(Wl+2al+1+bl+2+al)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-NDe4gkOg-1637814291073)(./1637807249073.png)]](https://i-blog.csdnimg.cn/blog_migrate/cd2d28d8f8da4b645a2ba45f0704c82a.png)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-BVXVOcDR-1637814291074)(./1637807496364.png)]](https://i-blog.csdnimg.cn/blog_migrate/48fc5343b2f98fbff898d911715d5ee2.png)
6. Densenet
DenseNet中,两个层之间都有直接的连接,因此该网络的直接连接个数为L(L+1)/2。
对于每一层,使用前面所有层的特征映射作为输入,并且使用其自身的特征映射作为所有后续层的输入
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-wM490NBS-1637814291074)(./1637807556579.png)]](https://i-blog.csdnimg.cn/blog_migrate/8a278132a3b8815dfe422af0d0798bb1.png)
5层的稠密块示意图:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-pyzatV7a-1637814291076)(./1637807576707.png)]](https://i-blog.csdnimg.cn/blog_migrate/978865c7b28dfde003770031a29b55c8.png)
DenseNets可以自然地扩展到数百个层,而没有表现出优化困难。在实验中,DenseNets随着参数数量的增加,在精度上产生一致的提高,而没有任何性能下降或过拟合的迹象。
优点:
- 缓解了消失梯度问题
- 加强了特征传播,鼓励特征重用
- 一定程度上减少了参数的数量
主要应用
图像处理领域
- 图像分类(物体识别):整幅图像的分类或识别
- 物体检测:检测图像中物体的位置进而识别物体
- 图像分割:对图像中的特定物体按边缘进行分割
- 图像回归:预测图像中物体组成部分的坐标
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-QRkDWH8t-1637814291077)(./1637807846241.png)]](https://i-blog.csdnimg.cn/blog_migrate/063abee4c759886614be97ebfe852cc4.png)
语音识别领域
- 将卷积神经网络的思想应用到语音识别的声学建模中,则可以利用卷积的不变性来克服语音信号本身的多样性。
自然语言处理领域
- 情感分析:分析文本体现的情感(正负向、正负中或多态度类型)
TextCNN 模型是由 Harvard NLP 组的 Yoon Kim 在2014年发表的 Convolutional Neural Networks for Sentence Classification 一文中提出的模型,由于 CNN 在计算机视觉中,常被用于提取图像的局部特征图,且起到了很好的效果,所以该作者将其引入到 NLP 中,应用于文本分类任务,试图使用 CNN 捕捉文本中单词之间的关系。
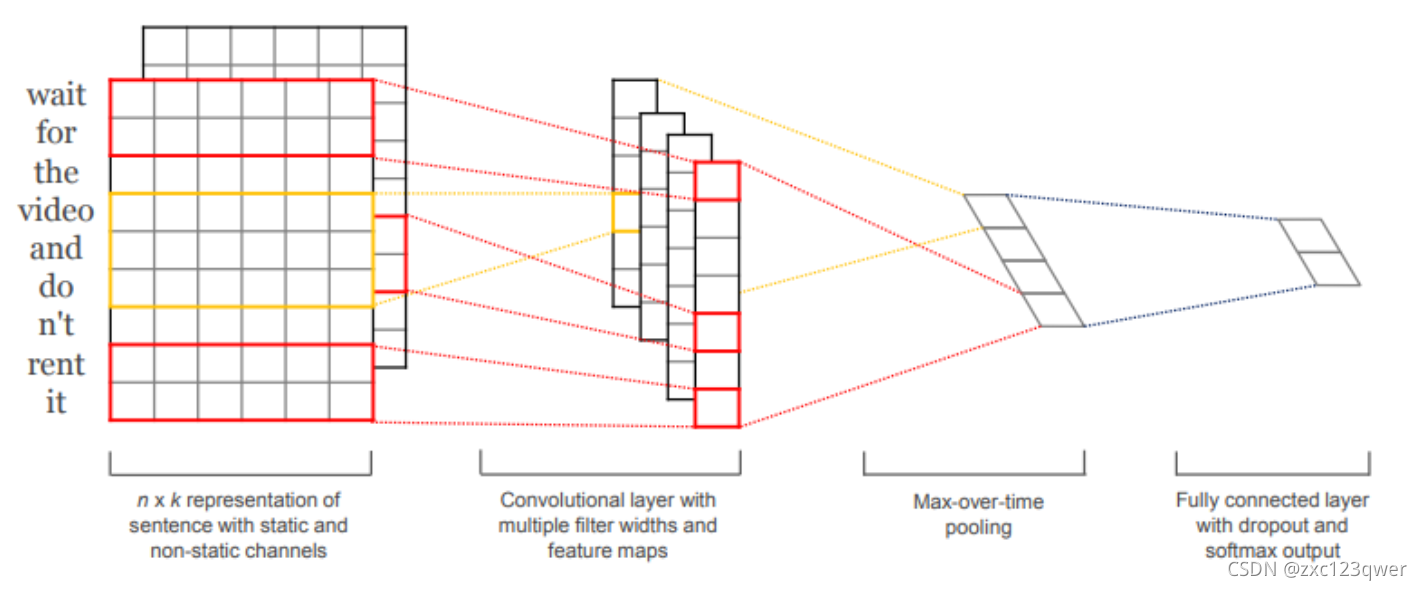




 本文概述了卷积神经网络(CNN)的起源,如何通过局部不变性提取图像特征,包括卷积、池化、各种卷积类型和常见网络结构,如LeNet、AlexNet、VGGNet和InceptionNet。重点介绍了参数训练、激活函数选择和深度学习在图像处理中的关键作用。
本文概述了卷积神经网络(CNN)的起源,如何通过局部不变性提取图像特征,包括卷积、池化、各种卷积类型和常见网络结构,如LeNet、AlexNet、VGGNet和InceptionNet。重点介绍了参数训练、激活函数选择和深度学习在图像处理中的关键作用。
















 1469
1469

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








