ML--决策树_根据信息增益的原则，构建决策树时第一个节点选择outlook特征创建了如上图的分支，请问下一步选择哪-优快云博客

本文链接：https://blog.youkuaiyun.com/zx_zhang01/article/details/82670781

决策树简介
在分类问题中，表示基于特征对实例进行分类，即定义在特征空间与类空间上的条件概率分布。
**优点：**决策树模型具有可读性，分类速度快，学习时，利用训练数据，根据损失函数最小化的原则。决策树的学习步骤分为：特征选择，决策树的生成，决策树的剪枝。本文主要针对特征选择和决策树的生成展开叙述。
决策树学习的思想主要来源于由Quinlan在1986年提出的ID3和1993年提出的C4.5算法，以及有Breiman等人在1984年提出的CART算法。

**决策树模型：**决策树由节点和有向边组成。内部结点表示一个特征或属性，叶结点表示一个类。、
下图即为决策树模型的示意图。
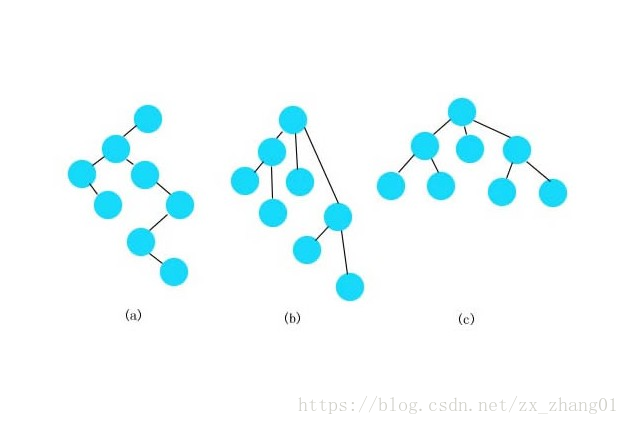
这里写图片描述
决策树与条件概率分布
假设X为表示特征的随机变量，Y为表示类的随机变量，那么这个条件概率分布可以表示为 $P (Y ∣ X)$ . X 取值于给定划分下的单元的集合，Y表示取值类的集合，各个叶结点上的取值会偏向某一个概率较大的类，决策树分类是将该结点的样本计算强行分到条件概率较大的那一边。
决策树学习
决策树学习，假定给定训练数据集：
$D=\left \{ (x_{1},y_{1}),(x_{2},y_{2}),\cdots ,(x_{N},y_{N})\right \}$ ,其中 $x_{i}=\left ( x_{i}^{1} ,x_{i}^{2},\cdots ,x_{i}^{n}\right )^{T}$ 为输入的样本，n代表特征的个数， $y_{i}\epsilon \left \{ 1,2,\cdots ,K \right \}$ 为类的标记， $i=1,2,\cdots ,N$ ,N为样本的容量，学习的目标是根据使决策树的损失函数为目标函数使其最小化，利用给定的训练集建一个决策树模型，使它能够对测试数据进行较好的分类。对未知的数据可能不会有较好的分类能力，最大可能就是发生过拟合（即受测试数据的“异常数据”的影响较大），在决策树中可以对其进行自下而上进行剪枝，本文不对此进行讨论，如诺感兴，敬请等待后续文章。
决策树是一个基于条件概率的分类模型，所以决策树的复杂度直接受决策树的大小影响，且对应局部最优解，决策树的剪枝对应全局最优解。
特征的选择
特征的选择在某种程度上直接决定着决策树的泛化能力，通常在决策树中的特征选择主要依靠于信息增益或者信息增益比（C4.5算法）

信息增益
再介绍信息增益之前，先简单的介绍一下熵和条件熵。
熵：表示随机变量不确定性，设x是一个取有限个值得离散随机变量其概率分布为

$P\left ( X=x_{i}\right )=p_{i}, i=1,2,\cdots ,n$

则随机变量的熵定义为

$H\left ( X \right )=-\sum_{i=1}^{n}p_{i}\log p_{i}$

,熵只依赖于X的分布，而与X的取值无关，熵值越大，随机变量的不确定性就越大.其范围为 $0\leq H\left ( X \right )\leq \log n$ 。条件熵： $H\left ( Y|X \right )$ 表示在已知随机变量X的情况下随机变量Y的不确定性。定义为X给定条件下Y的条件概率分布分熵对X的数学期望：

$H\left ( Y|X \right )=\sum_{i=1}^{n}p_{i}H\left ( Y|X=x_{i} \right )$

其中 $p_{i}=P\left ( X=x_{i} \right ),i=1,2,\cdots ,n.$ . 信息增益表示得知特征X的信息后降低类别Y的信息的不确定性。定义：信息增益：特征A对训练数据集D的信息增益 $g\left ( D,A \right )$ ，定义为集合D的经验熵 $H\left ( D \right )$ 与特征A给定条件下的经验条件熵 $H\left ( D|A \right )$ 之差，即

$g\left ( D,A \right )=H\left ( D \right )-H\left ( D|A \right )$

决策树的信息增益等价于训练数据集中类和特征的信息。 **信息增益** 设训练数据集为D,|D|表示样本的个数，设有K个类 $C_{k}$ , $k=1,2,\cdots ,K$ ， $|C_{k}|$ 表示属于第k类的样本个数，其中 $\sum_{k=1}^{K}|C_{k}|=|D|$ ，设特征A有n个不同的取值 $\left \{ a_{1},a_{2},\cdots ,a_{n} \right \}$ ，根据特征A的取值将D划分为n个子集 $\left \{ D_{1},D_{2},\cdots D_{n} \right \}$ ， $|D_{i}|$ 表示属于第i个特征的样本个数，其中 $\sum_{i=1}^{n}|D_{i}|=|D|$ ，子集 $D_{i}$ 中属于第k类的样本表示为 $D_{ik}$ , 即 $D_{ik}=D_{i}\bigcap C_{k}$ , $|D_{ik}|$ 表示为 $D_{ik}$ 的样本个数。 **信息增益的计算：** （1）计算机数据集D的经验熵 $H\left ( D \right )$

$H\left ( D \right )=-\sum_{k=1}^{K}\frac{|C_{k}|}{|D|}\log \frac{|C_{k}|}{|D|}$

(2) 计算特征A对数据集D的经验条件熵 $H\left ( D|A \right )$

$H\left ( D|A \right )\sum_{i=1}^{n}\frac{|D_{i}|}{|D|}H\left ( D_{i} \right )=-\sum_{i=1}^{n}\frac{|D_{i}|}{|D|}\sum_{k=1}^{K}\frac{|D_{ik}|}{|D_{i}|}\log _{2}\frac{|D_{ik}|}{|D_{i}|}$

(3)计算信息增益熵 $g\left ( D,A \right )$

$g\left ( D,A \right )=H\left ( D \right )-H\left ( D|A \right )$

讲过原理之后，我们就拿身边的一些事情开刀喽！

下表是一个有12个样本组成的逃课样本数据
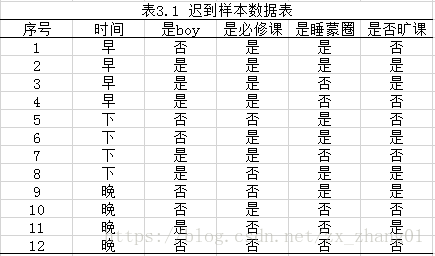
这里写图片描述
对表所给出的数据集D，根据信息增益的原则选择出特征最优
计算信息熵：

$H\left ( D \right )=1$

然后根据各个特征对数据集的增益，分别以 $A_{1},A_{2},A_{3},A_{4}$ 表示时间，是否是boy,是主修课，是睡蒙圈4个特征 (1) $g\left ( D,A_{1} \right )=H\left ( D \right )-\frac{1}{3}\left ( -\frac{1}{2}\log _{2}\frac{1}{2}-\frac{1}{2}\log _{2}\frac{1}{2} \right )$

$-\frac{1}{3}\left ( -\frac{1}{2}\log _{2}\frac{1}{2}-\frac{1}{2}\log _{2}\frac{1}{2} \right )$ $-\frac{1}{3}\left ( -\frac{1}{2}\log _{2}\frac{1}{2}-\frac{1}{2}\log _{2}\frac{1}{2} \right )$

=0 这里分别是 $D_{1},D_{2},D_{3},$ 分别是D取值为早，中，晚的样本的子集。（2） $g\left ( D,A_{1} \right )=H\left ( D \right )-\frac{7}{12}\left ( -\frac{4}{7}\log _{2}\frac{3}{7}-\frac{3}{7}\log _{2}\frac{3}{7} \right )$

$-\frac{5}{12}\left ( -\frac{2}{5}\log _{2}\frac{2}{5}-\frac{3}{5}\log _{2}\frac{3}{5} \right )$

=0.029 (3) $g\left ( D,A_{3} \right )=H\left ( D \right )-\frac{7}{12}\left ( -\frac{4}{7}\log _{2}\frac{4}{7}-\frac{4}{7}\log _{2}\frac{4}{7} \right )$

$-\frac{5}{12}\left ( -\frac{3}{5}\log _{2}\frac{3}{5}-\frac{2}{5}\log _{2}\frac{2}{5} \right )$

= 0.025 (4) $g\left ( D,A_{4} \right )=H\left ( D \right )-H\left ( D|A_{4} \right )=1-0.0918=0.082$ 最后比较各特征的信息增益的大小，由于特征 $A_{4}$ （代表是否睡蒙圈）的信息增值最大，所以选择其作为最优特征，由此可见在是否是必修课的情况下，睡蒙圈占有了主导地位，所以希望老师可以体谅我们一下，不是我们不爱学习。