HDU-1710二叉树，给前中序求后序

由题目（也是基础知识），二叉树的遍历如下：
二叉树遍历：
对一棵二叉树进行遍历，我们可以采取3中顺序进行遍历，分别是前序遍历、中序遍历和后序遍历。这三种方式是以访问父节点的顺序来进行命名的。假设父节点是N，左节点是L，右节点是R，那么对应的访问遍历顺序如下：

前序遍历 N－>L－>R

中序遍历 L－>N－>R

后序遍历 L－>R－>N

所以，对于以下这棵树，三种遍历方式的结果是：

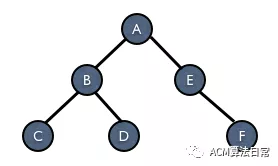
::: 前序遍历 ABCDEF

::: 中序遍历 CBDAEF

::: 后序遍历 CDBFEA

思路：
题目里给了前序和中序，我们可以知道，前序的第一个肯定是根，在中序中找到根的位置n，n左边的就是左子树，右边的就是右子树（根据上面说的中序遍历），那么再由前序遍历的定义，我们得知2-n+1就是左子树（前序），剩下的就是右子树，再分析前序里的左子树，左子树最左面的肯定又是一个根（只不过他不是最上面的根儿，叫他分根），再像上面一样操作，你会发现，这不就是递归嘛，我们就按上面的步骤进行递归

递归方程：

int build(int L1,int R1,int L2,int R2)//L1,R1是前序左右范围，L2，R2中序
{
	if(L1 > R1) return 0;
	int root = pre_order[L1];//前序第一个为根
	int p = L2;
	while(in_order[p] != root) p++;//找到中序的根
	int cnt = p-L2;
	lch[root] = build(L1+1,L1+cnt,L2,L2+cnt-1);//构建左子树
	rch[root] = build(L1+cnt+1,R1,p+1,R2);//构建右子树
	return root;
}

然后用lch，rch数组构建二叉树，最后用递归求后序遍历
先左边，再右边，后中间

void dfs(int l)
{
	if(lch[l]) dfs(lch[l]); //左边
	if(rch[l]) dfs(rch[l]);//右边
	
	a.push_back(l);//中间
	return;
}

最后ac代码是：

#include<cstdio>
#include<iostream>
#include<queue>
#include<algorithm>
#include<cstring>
#include<vector>
using namespace std;
const int maxn = 1000+8;

int N;
int pre_order[maxn],in_order[maxn];
int lch[maxn],rch[maxn];
vector<int> a;

int build(int L1,int R1,int L2,int R2)
{
	if(L1 > R1) return 0;
	int root = pre_order[L1];
	int p = L2;
	while(in_order[p] != root) p++;
	int cnt = p-L2;
	lch[root] = build(L1+1,L1+cnt,L2,L2+cnt-1);
	rch[root] = build(L1+cnt+1,R1,p+1,R2);
	return root;
}

void dfs(int l)
{
	if(lch[l]) dfs(lch[l]);
	if(rch[l]) dfs(rch[l]);
	
	a.push_back(l);
	return;
}

int main()
{
	while(cin>>N)
	{
		memset(lch,0,sizeof(lch));
		memset(rch,0,sizeof(rch));
		
		for(int i = 0; i < N; i++) cin>>pre_order[i];
		for(int i = 0; i < N; i++) cin>>in_order[i];
		
		int root = build(0,N-1,0,N-1);
		a.clear();
		
		dfs(root);
		for(int cnt = 0; cnt < a.size(); cnt++)
	    {
	    	if(cnt == 0) cout<<a[cnt];
	    	else cout<<" "<<a[cnt];
		}
		cout<<endl;
	}
	return 0;
}

奥利给，干了兄弟们！