ML Lecture0-introduction of Machine Learning
一、机器学习是什么?
Looking for a Function From Data
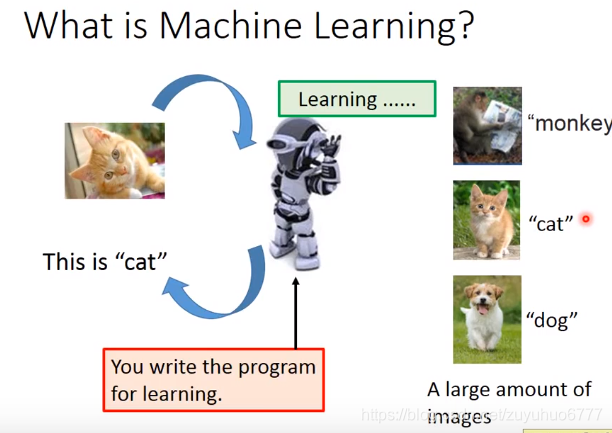

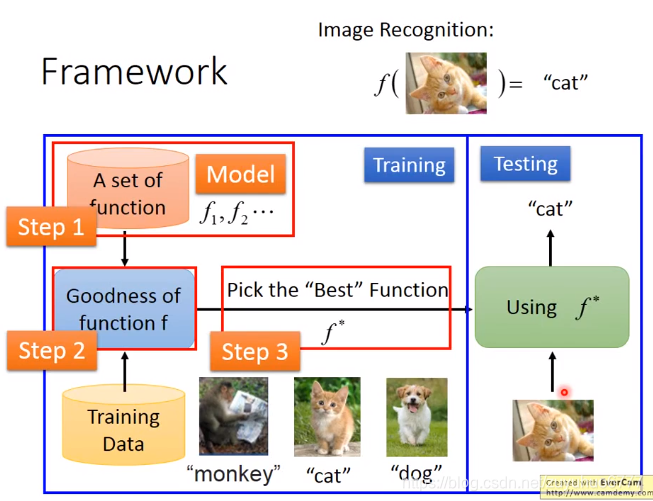
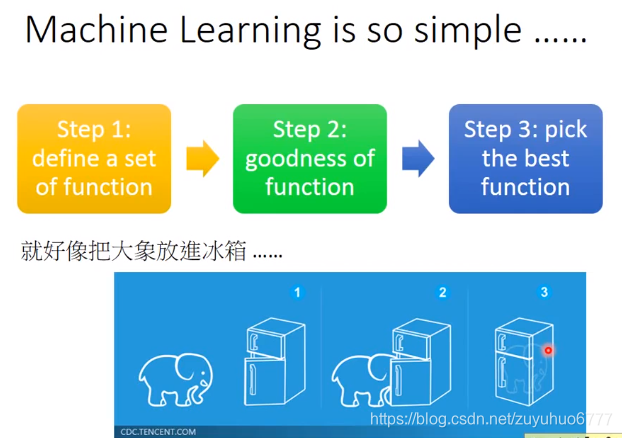
三个步骤:定义-train-挑出最好的
二、学习的内容(Learning Map)
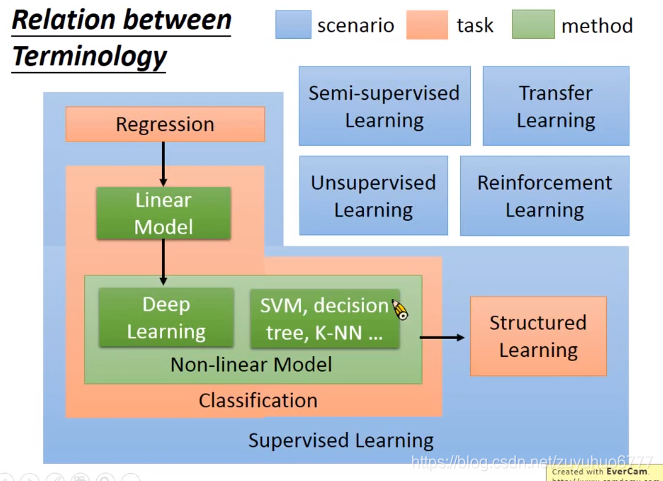
supervised Learning 需要Training data input/label
semi-supervised 有一些没有标签的数据
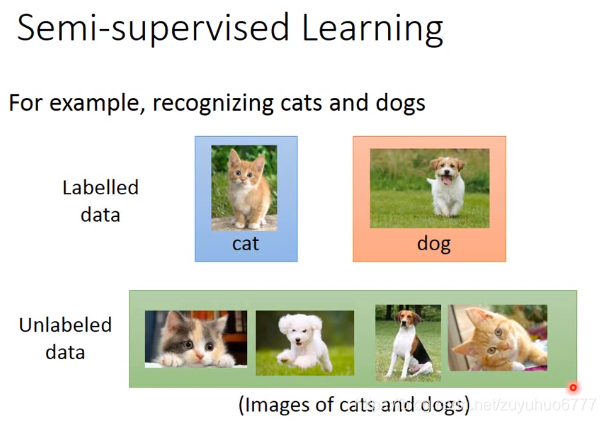
一些无关的数据(里面既有有标签,也有没标签的)Transfer Learning

unsupervisde learning

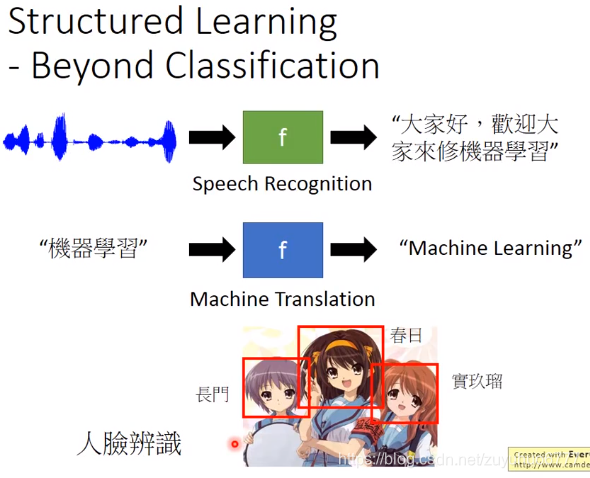
Structured Learning 输出有结构性的东西
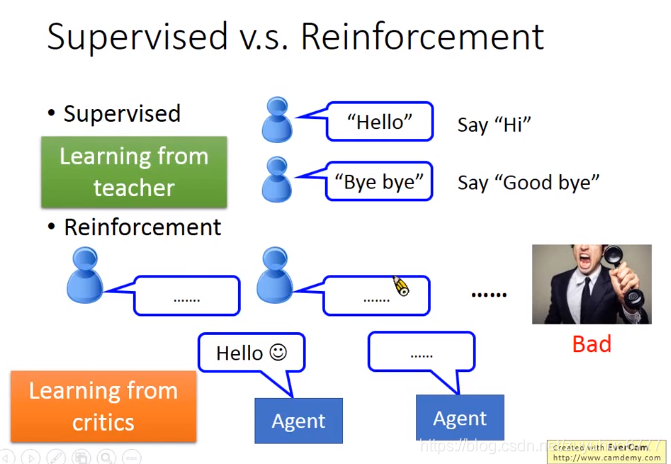
学校与社会学习的区别,从评价中学习
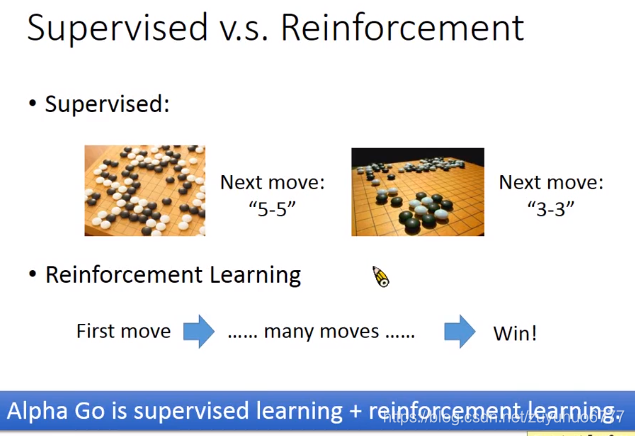
ML Lecture 1 Regression
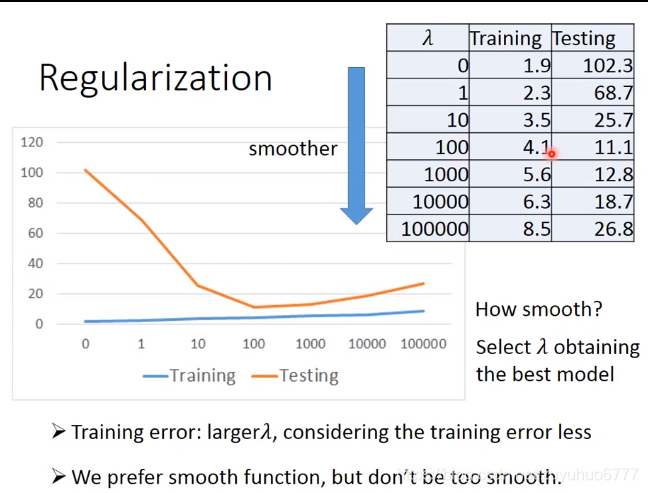
由一次到二次。。逐次增加模型的复杂度,但是测试集的结果可能会变差,过拟合了

Back to step2:正则化(Regularization):重新定义loss

喜欢平滑一点的function
二、
-
学习中心极限定理,
中心极限定理指的是给定一个任意分布的总体。我每次从这些总体中随机抽取 n 个抽样,一共抽 m 次。 然后把这 m 组抽样分别求出平均值。 这些平均值的分布接近正态分布。
参考:https://zhuanlan.zhihu.com/p/25241653
-
学习正态分布
是一种连续型的概率分布,随机变量服从概率密度函数,均值为u,方差为
-
学习最大似然估计
极大似然估计,通俗理解来说,就是利用已知的样本结果信息,反推最具有可能(最大概率)导致这些样本结果出现的模型参数值!
换句话说,极大似然估计提供了一种给定观察数据来评估模型参数的方法,即:“模型已定,参数未知”
参考:https://zhuanlan.zhihu.com/p/26614750
-
推导回归Loss function
Model:
L2 Loss Fuction: (
为样本点计数)
为训练集真实输出,
为训练集特征值,
为特征对应的权重,
为偏置值,
为预测值。
-
学习损失函数与凸函数之间的关系
在无约束损失函数优化问题中,如果损失函数在所属凸集上为凸函数且可微,则可以通过梯度下降法找到全局最小值;否则,根据初始点的选择不同,只能在其小邻域内寻找局部最小值。
-
了解全局最优和局部最优
对于严格凸函数来说,局部最优=全局最优;
对于非凸函数来说,在局部可微的前提下,可以找到多个局部最优解,但很难确定其是否为全局最优。
-
学习导数,泰勒展开
导数:一个函数在某一点的导数描述了这个函数在这一点附近的变化率。

参考:https://www.zhihu.com/question/25627482
上文中有一处错误,少了一个平方,评论里面有提到
-
推导梯度下降公式
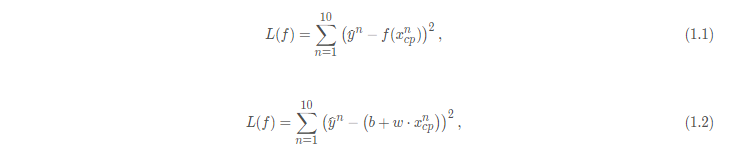

-
写出梯度下降的代码
# -*- coding: utf-8 -*-
"""
Created on Mon May 13 20:42:20 2019
@author: xuhaohao
"""
from sympy import *
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np
import random
class GradientDescent:
def __init__(self, eta=0.01, iter_num=1000, stop_condition=0.01):
self.eta = eta # 学习率
self.iter_num = iter_num # 迭代次数
self.stop_condition = stop_condition # 停止条件
self.x1, self.x2 = symbols('x1, x2')
self.x_1 = np.arange(-50, 50, 0.05)
self.x_2 = np.arange(-50, 50, 0.05)
def function(self):
'''定义函数'''
y = 10 * self.x1**2 + 20 * self.x2**2 + 5
return y
# result: 10*x1**2 + 20*x2**2 + 5
def plot_3d(self):
'''绘制y的曲面图'''
x_1, x_2 = np.meshgrid(self.x_1, self.x_2)
y_ = np.zeros(x_1.shape)
for i in range(2000):
for j in range(2000):
y_[i, j] = 10 * x_1[i, j] ** 2 + 20 * x_2[i, j] ** 2 + 5
fig = plt.figure()
ax = Axes3D(fig)
ax.plot_surface(x_1, x_2, y_, cmap='rainbow')
plt.xlabel('x1')
plt.ylabel('x2')
plt.show()
def gradientdescent(self):
# 随机选择初始点
x1_0 = random.randint(40, 50) * (-1)**random.randint(0, 2)
x2_0 = random.randint(40, 50) * (-1)**random.randint(0, 2)
print('随机选择初始点:(%d, %d)' % (x1_0, x2_0))
# 调用定义的函数y
y = self.function()
k = 1
while k <= self.iter_num:
x1_n = x1_0 - self.eta * diff(y, self.x1, 1).subs(self.x1, x1_0)
x2_n = x2_0 - self.eta * diff(y, self.x2, 1).subs(self.x2, x2_0)
x1_0, x2_0 = x1_n, x2_n
nabla_L = [int(diff(y, self.x1, 1).subs(self.x1, x1_0)), int(diff(y, self.x2, 1).subs(self.x2, x2_0))]
# 如果梯度2范数小于定义的极小值,则停止迭代
if np.linalg.norm(nabla_L) <= self.stop_condition:
print('迭代次数:%d' % k)
print('迭代全局最小值:(%d, %d, %d)' % (x1_0, x2_0, y.subs({self.x1:x1_0, self.x2:x2_0})))
break
k += 1
a = GradientDescent()
a.plot_3d()
a.function()
a.gradientdescent()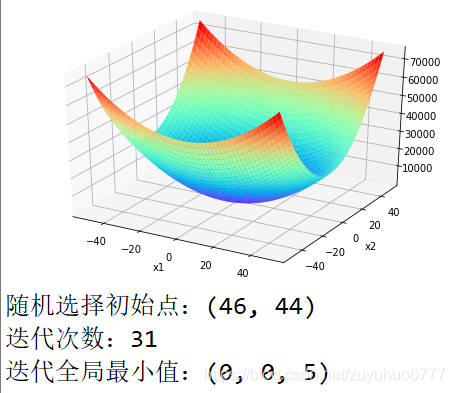
-
学习L2-Norm,L1-Norm,L0-Norm
L0范数:L0范数不是真正的范数,它是用来度量向量中非零元素的个数,如果使用L0范数来约束参数矩阵w的数值,就是希望参数w的大部分元素都是0,让参数矩阵稀疏化,一般不用L0作正则化,用L1正则代替。
L1范数:指向量中各元素绝对值之和
L2范数:指各元素的平方和再开平方,可以使参数矩阵w的每个元素值都接近0,使曲线更加平滑
-
推导正则化公式
正则化就是在计算损失函数时对参数的值进行限定,损失函数被重新定义为
,正则项的限制使曲线变得平滑
-
说明为什么用L1-Norm代替L0-Norm
普遍用L1代替L0做稀疏约束,主要因为在一定条件下L1与L0求解目标等价,但L1是L0的最优凸近似,易于优化求解。
参考:https://blog.csgrandeur.com/blogs/20170329-about-norm
-
学习为什么只对w/Θ做限制,不对b做限制
loss function中加入正则项对w进行限制是为了使曲线变得平滑,而调整b的大小跟曲线的平滑无关,b的大小只是对曲线进行上下移动。
























 534
534

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








