李宏毅机器学习-01

中心极限定理

给定一个总体，每次从中抽取等量样本。当抽取样本的次数充分大时，样本均值的分布接近静正态分布。

正态分布

若随机变量X服从一个数学期望为μ、方差为σ^2 的正态分布：

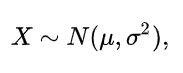
则其概率密度函数为：

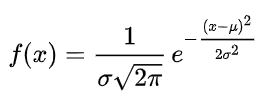
正态分布的数学期望值或期望值μ等于位置参数，决定了分布的位置；其方差σ^2 的开平方或标准差σ等于尺度参数，决定了分布的幅度。

极大似然估计

根据样本结果推测位置参数的大概值，如果此参数能使样本出现的概率最大，则把这个参数作为估计的真实值。
步骤：

1. 写出似然函数
2. 对似然函数取对数
3. 求导，得到极值点
4. 选择极大值点

回归Loss function的推导

。。。。。。

损失函数与凸函数之间的关系

如果损失函数为凸函数，其极值就为最优解；反之，损失函数可能只计算得到局部最优解，很难得到全局最优 。

全局最优和局部最优

我们根据损失函数来使用梯度下降算法时，最后得到的极值点可能是局部极值点，而不是全局极值点。如果损失函数为凸函数的话就能避免这个问题。

泰勒展开

泰勒公式是将一个在x=x0处具有n阶导数的函数f(x)利用关于(x-x0)的n次多项式来逼近函数的方法。
若函数f(x)在包含x0的某个闭区间[a,b]上具有n阶导数，且在开区间(a,b)上具有(n+1)阶导数，则对闭区间[a,b]上任意一点x，成立下式：

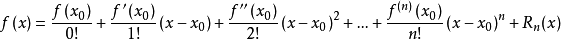
其中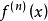，表示f(x)的n阶导数，等号后的多项式称为函数f(x)在x0处的泰勒展开式，剩余的Rn(x)是泰勒公式的余项，是(x-x0)n的高阶无穷小。

梯度下降代码

def batchGradientDescent(x, y, theta, alpha, m, maxIterations):
	data = []
	for i in range(4):
		data.append(i)
    xTrains = x.transpose()
    for i in range(0, maxIterations):
        hypothesis = np.dot(x, theta)
        loss = hypothesis - y
        index = random.sample(data, 1)
        index1 = index[0]
        gradient = loss[index1]*x[index1]
        theta = theta - alpha * gradient
    return theta

L2-Norm, L1-Norm, L0-Norm

为什么用L1-Norm代替L0-Norm

虽然L0正则优势很明显，但求解困难属于NP问题，因此一般情况下引入L0正则的最近凸优化L1正则（方便求解）来近似求解并同样可实现稀疏效果。

为什么只对w/Θ做限制，不对b做限制

因为b是一个常数，只会然函数值整体上下移动，不会改变函数的全局最优点。