1. 问题(为什么要使用PCA)
真实的训练数据总是存在各种各样的问题:
1、 比如拿到一个汽车的样本,里面既有以“千米/每小时”度量的最大速度特征,也有“英里/小时”的最大速度特征,显然这两个特征有一个多余。
2、 拿到一个数学系的本科生期末考试成绩单,里面有三列,一列是对数学的兴趣程度,一列是复习时间,还有一列是考试成绩。我们知道要学好数学,需要有浓厚的兴趣,所以第二项与第一项强相关,第三项和第二项也是强相关。那是不是可以合并第一项和第二项呢?
3、 拿到一个样本,特征非常多,而样例特别少,这样用回归去直接拟合非常困难,容易过度拟合。比如北京的房价:假设房子的特征是(大小、位置、朝向、是否学区房、建造年代、是否二手、层数、所在层数),搞了这么多特征,结果只有不到十个房子的样例。要拟合房子特征->房价的这么多特征,就会造成过度拟合。
4、 这个与第二个有点类似,假设在IR中我们建立的文档-词项矩阵中,有两个词项为“learn”和“study”,在传统的向量空间模型中,认为两者独立。然而从语义的角度来讲,两者是相似的,而且两者出现频率也类似,是不是可以合成为一个特征呢?
5、 在信号传输过程中,由于信道不是理想的,信道另一端收到的信号会有噪音扰动,那么怎么滤去这些噪音呢?
回顾我们之前介绍的《模型选择和规则化》,里面谈到的特征选择的问题。但在那篇中要剔除的特征主要是和类标签无关的特征。比如“学生的名字”就和他的“成绩”无关,使用的是互信息的方法。
而这里的特征很多是和类标签有关的,但里面存在噪声或者冗余。在这种情况下,需要一种特征降维的方法来减少特征数,减少噪音和冗余,减少过度拟合的可能性。
下面探讨一种称作主成分分析(PCA)的方法来解决部分上述问题。PCA的思想是将n维特征映射到k维上(k<n),这k维是全新的正交特征。这k维特征称为主元,是重新构造出来的k维特征,而不是简单地从n维特征中去除其余n-k维特征。
2、PCA计算过程
首先介绍PCA的计算过程:
假设我们得到的2维数据如下:
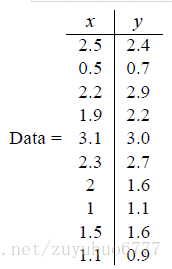
行代表了样例,列代表特征,这里有10个样例,每个样例两个特征。
第一步分别求x和y的平均值,然后对于所有的样例,都减去对应的均值。这里x的均值是1.81,y的均值是1.91,那么一个样例减去均值后即为(0.69,0.49),得到
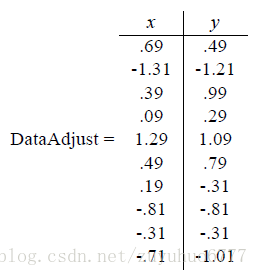
第二步,求特征协方差矩阵,如果数据是3维,那么协方差矩阵是
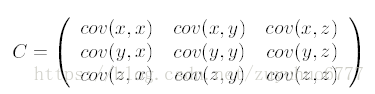
这里只有x和y,求解得
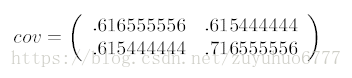
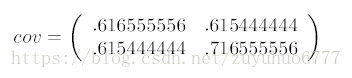
对角线上分别是x和y的方差,非对角线上是协方差。协方差大于0表示x和y若有一个增,另一个也增;小于0表示一个增,一个减;协方差为0时,两者独立。协方差绝对值越大,两者对彼此的影响越大,反之越小。
第三步,求协方差的特征值和特征向量,得到
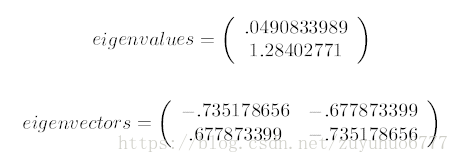
上面是两个特征值,下面是对应的特征向量,特征值0.0490833989对应特征向量为![]() ,这里的特征向量都归一化为单位向量。
,这里的特征向量都归一化为单位向量。
第四步,将特征值按照从大到小的顺序排序,选择其中最大的k个,然后将其对应的k个特征向量分别作为列向量组成特征向量矩阵。
这里特征值只有两个,我们选择其中最大的那个,这里是1.28402771,对应的特征向量是![]() 。
。
第五步,将样本点投影到选取的特征向量上。假设样例数为m,特征数为n,减去均值后的样本矩阵为DataAdjust(m*n),协方差矩阵是n*n,选取的k个特征向量组成的矩阵为EigenVectors(n*k)。那么投影后的数据FinalData为
这里是
FinalData(10*1) = DataAdjust(10*2矩阵)×特征向量![]()
得到结果是

这样,就将原始样例的n维特征变成了k维,这k维就是原始特征在k维上的投影。
3、 总结和讨论
PCA技术的一大好处是对数据进行降维的处理。我们可以对新求出的“主元”向量的重要性进行排序,根据需要取前面最重要的部分,将后面的维数省去,可以达到降维从而简化模型或是对数据进行压缩的效果。同时最大程度的保持了原有数据的信息。
PCA技术的一个很大的优点是,它是完全无参数限制的。在PCA的计算过程中完全不需要人为的设定参数或是根据任何经验模型对计算进行干预,最后的结果只与数据相关,与用户是独立的。
但是,这一点同时也可以看作是缺点。如果用户对观测对象有一定的先验知识,掌握了数据的一些特征,却无法通过参数化等方法对处理过程进行干预,可能会得不到预期的效果,效率也不高。
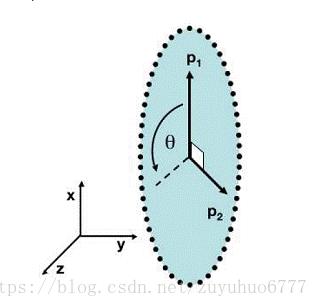
图表 4:黑色点表示采样数据,排列成转盘的形状。 容易想象,该数据的主元是![]() 或是旋转角
或是旋转角![]() 。
。
如图表 4中的例子,PCA找出的主元将是![]() 。但是这显然不是最优和最简化的主元。
。但是这显然不是最优和最简化的主元。![]() 之间存在着非线性的关系。根据先验的知识可知旋转角
之间存在着非线性的关系。根据先验的知识可知旋转角![]() 是最优的主元(类比极坐标)。则在这种情况下,PCA就会失效。但是,如果加入先验的知识,对数据进行某种划归,就可以将数据转化为以
是最优的主元(类比极坐标)。则在这种情况下,PCA就会失效。但是,如果加入先验的知识,对数据进行某种划归,就可以将数据转化为以![]() 为线性的空间中。这类根据先验知识对数据预先进行非线性转换的方法就成为kernel-PCA,它扩展了PCA能够处理的问题的范围,又可以结合一些先验约束,是比较流行的方法。
为线性的空间中。这类根据先验知识对数据预先进行非线性转换的方法就成为kernel-PCA,它扩展了PCA能够处理的问题的范围,又可以结合一些先验约束,是比较流行的方法。
有时数据的分布并不是满足高斯分布。如图表 5所示,在非高斯分布的情况下,PCA方法得出的主元可能并不是最优的。在寻找主元时不能将方差作为衡量重要性的标准。要根据数据的分布情况选择合适的描述完全分布的变量,然后根据概率分布式
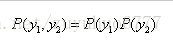
来计算两个向量上数据分布的相关性。等价的,保持主元间的正交假设,寻找的主元同样要使![]() 。这一类方法被称为独立主元分解(ICA)。
。这一类方法被称为独立主元分解(ICA)。
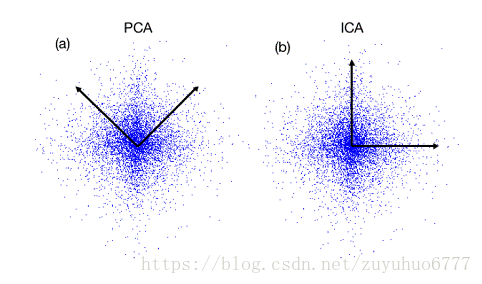
图表 5:数据的分布并不满足高斯分布,呈明显的十字星状。
这种情况下,方差最大的方向并不是最优主元方向。
另外PCA还可以用于预测矩阵中缺失的元素。
4. 其他参考文献A Tutorial on Principal Component Analysis J Shlens
5、代码
matlab 代码:https://download.youkuaiyun.com/download/zuyuhuo6777/10497736
如果你觉得该帖子帮到你了,还望贵人多多支持,鄙人会再接再厉,继续努力的





 本文介绍了主成分分析(PCA)的基本概念及其在数据降维中的应用。PCA能够将高维数据映射到低维空间,去除冗余特征并降低过拟合风险。文中详细解释了PCA的计算步骤,并讨论了其在不同场景下的优势与局限。
本文介绍了主成分分析(PCA)的基本概念及其在数据降维中的应用。PCA能够将高维数据映射到低维空间,去除冗余特征并降低过拟合风险。文中详细解释了PCA的计算步骤,并讨论了其在不同场景下的优势与局限。
















 3386
3386

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








