机器学习随记【day02-03】

课程中会用到的符号
m = Number of training examples 训练样本的数量
x’s =“input” variable / features 输入特征
y’s = “output” variable /"target"variable 输出变量
(x,y) =one training example 一个训练样本
(x^ (i),y^ (i) ) 第i个训练样本，i不是幂指数，而是索引

模型描述

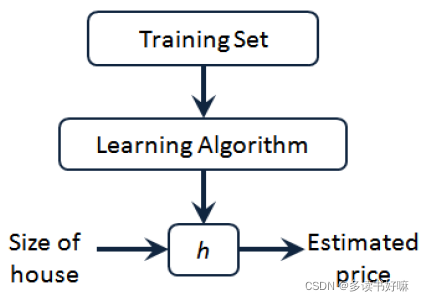
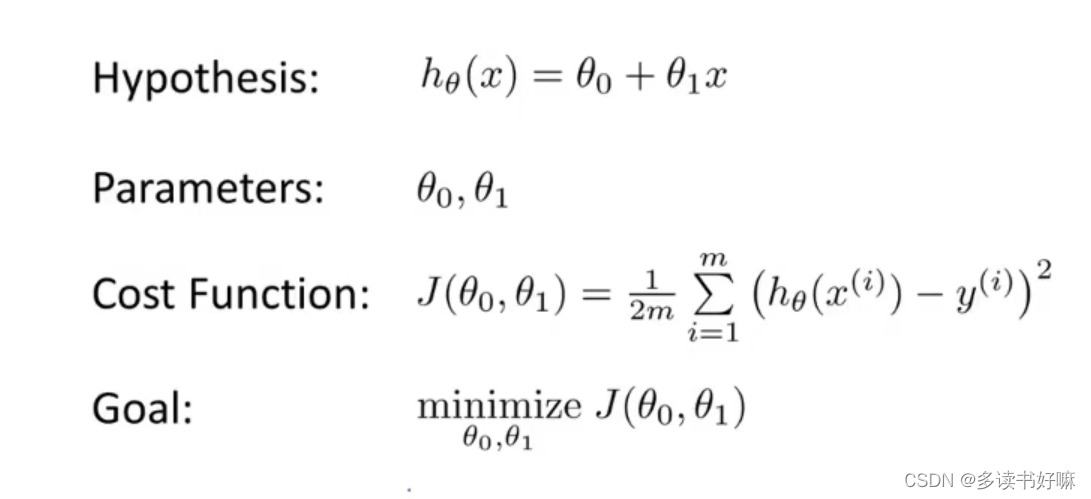
假设函数h(hypothesis)

是一个从输入到输出的映射
hθ (x)=θ0+θ1*x
上图中把房子大小作为输入变量(输入的x)，他会输出相应预测值(输出的y)

代价函数

代价函数J(θ)，图中为J(θ1,θ2) [平方误差代价函数]，m为样本容量，训练目标是为了让J(θ)最小。
/2是为了消除求导后的2，对结果无影响，只是优化了后续计算，/m则是消除样本容量对结果数值的影响。

假设函数与代价函数的直观体会

θ0=0 (即只有θ1一个变量)
这里m=3，根据公式代入容易求得：
J(1)=0;
J(0.5)≈0.58
J(0)≈2.3
形如二次，实际不是，视频里称 “bowl-like shape (碗状)”

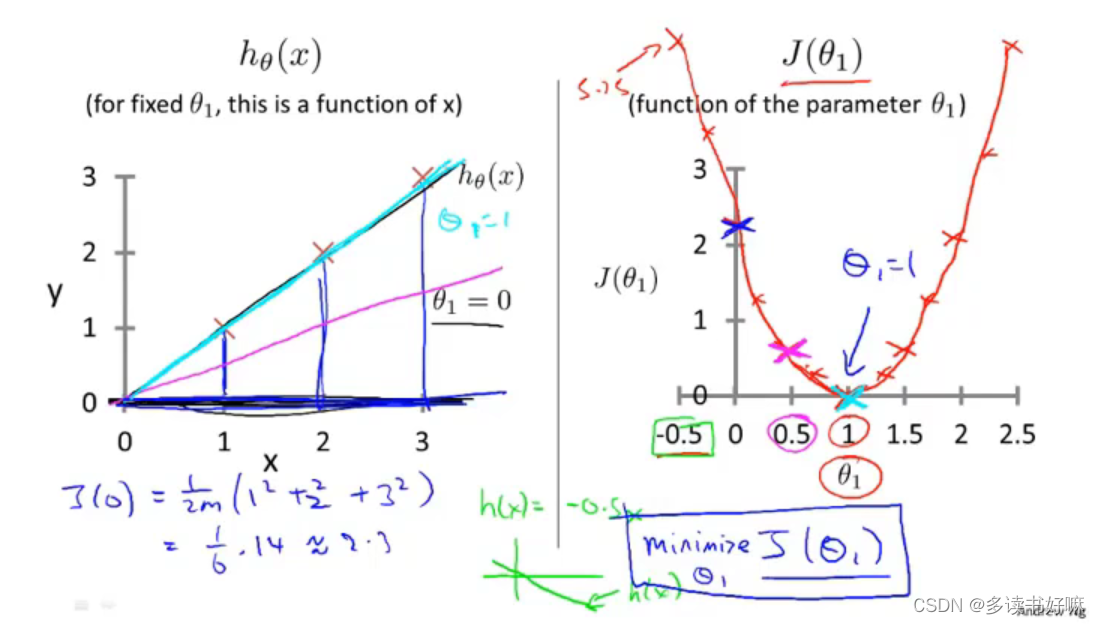
不限定θ0

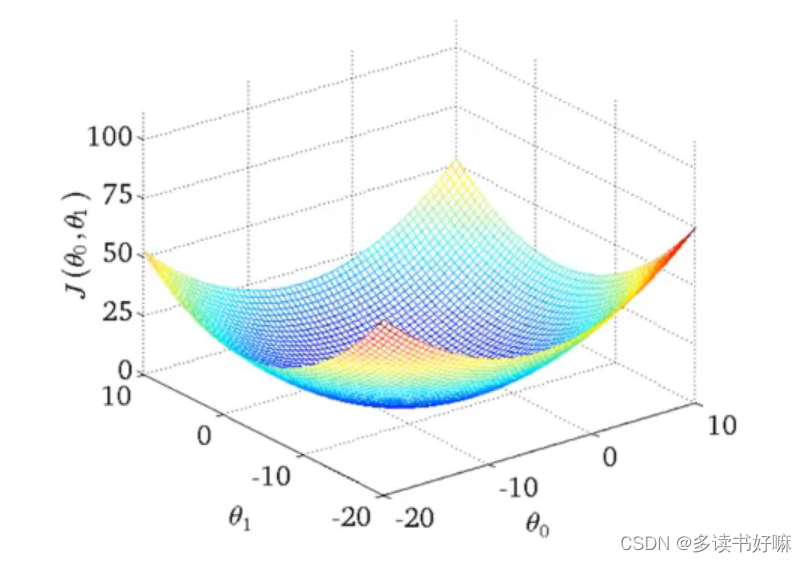
容易看出若限定了θ0，J(θ1)也是“碗状”的

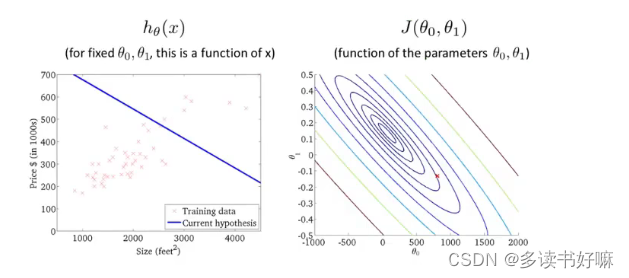
如果把上面的3D图”拍“到平面上，则有这样的等高图，也是代价函数的另一种表达形式

梯度下降

问题概述
(注意，此时J是一般函数)
做法是初始化θ0、θ1 ，然后一直改变θ0、θ1，使J最小。
(局部最优求全局最优，很难不想到贪心算法）

数学原理

α：learning rate 学习率，决定每一次改变的幅度
":=" 表示赋值
式子表示对θ0、θ1进行更新
注意：此更新是“无序的”，即先将θi更新值赋给tempi，再将tempi赋给θi，避免直接赋值影响其他变量的更新赋值。

下面展示错误的更更新方式：