kmeans的过程
kmeans的过程如下图所示

第一步:从M个对象中任意选择2个对象作为初始聚类的中心,如上图(b)所示。
第二步:计算每个对象到聚类中心的距离,把各个样本划分到与他们最近的中心所代表的类别中去,如图©所示。并且计算当前状态下的损失。
第三步:计算各类别所包含点的均值点,将其作为新的类别中心。如(d)所示。
第四步:重复第二步和第三步,知道连续的两次的损失值相差为某一设定值为止。
kmeans的原理
kmeans的聚类的过程中涉及四个关键点:k值的选择(就是聚几个类,这是超参数,需要人为给定),初始值,距离度量方式,损失函数。
第一,k值的选择
由于是超参数的原因,所以k值的选择依据你需要聚类的数目进行选择了。
第二,初始值
传统的kmeans使用的是随机选择。也有算法的优化,后面总结。
第三,距离度量方式
距离度量方式最多的还是欧式距离。

第四,损失函数
聚类问题的损失函数就是各个样本向量到对应簇均值向量的均方误差,假设样本点(x1,x2,……,xn)需要被聚类为k个簇(C1,C2,……,Ck),则各个簇内样本点的均值向量为:
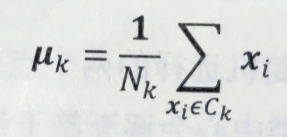
其中,Nk为簇Ck中包含的样本数目,所有簇的总均方误差为:

kmeans的例子
上面过程看着还是有一些复杂,我们看一个例子。
假设我们有以下几个点:
| x | y | |
|---|---|---|
| p1 | 0 | 0 |
| p2 | 1 | 2 |
| p3 | 3 | 1 |
| p4 | 8 | 8 |
| p5 | 9 | 10 |
| p6 | 10 | 7 |
首先第一步,我们要选择聚为几类,这次我们将其聚类为2类,即k选为2
接着第二步,我们需要随机选择起始点,我们就选p1和p2吧。
接着第三步,距离的度量,欧式距离,我们算一下
| p1(0,0) | p2(1,2) | |
|---|---|---|
| p3 | 3.16 | 2.24 |
| p4 | 11.13 | 9.22 |
| p5 | 13.45 | 11.31 |
| p6 | 12.21 | 10.30 |
算出来p3,4,5,6和节点p1p2之间的距离后,我们看一下离谁近就将节点划分过去。p3和p2近,p4也和p2近,p5也是,p6也是。那么这次就被分为了两类。第一类:p1。第二类:p2,p3,p4,p5,p6
接着我们需要迭代了,因为我们需要达到损失函数的要求。这一轮迭代需要再选择中心,但是不是随机选择了,需要计算分类的中心,就是这次的中心是计算出来的。第一类就一个点,怎么计算也就是它了。第二类的坐标应该分别是(1+3+8+9+10)/5,(2+1+8+10+7)/5.即两个坐标是:(6.2,5.6)。
我们需要接着计算p2,3,4,5,6,到p1和(6.2,5.6)之间的距离。
| (0,0) | (6.2,5.6) | |
|---|---|---|
| p2 | 2.24 | 6.32 |
| p3 | 3.16 | 5.6 |
| p4 | 11.13 | 3 |
| p5 | 13.45 | 5.22 |
| p6 | 12.21 | 4.05 |
我们这次算出来的分组应该是这样的,第一组:p1,p2,p3。第二组:p3,p4,p5.
我们还需要接着迭代下去,还是计算出对应分组的两个点,第一个点为(0+1+3)/3,(0+2+1)/3,即点为(1.33,1).第二个点为(8+9+10)/3,(8+10+7)/3,即点为(9,8.33)
继续算一下各个点到这两个点之间的距离
| (1.33,1) | (9,8.33) | |
|---|---|---|
| p1 | 1.66 | 12.26 |
| p2 | 1.05 | 10.2 |
| p3 | 2.33 | 9.47 |
| p4 | 9.67 | 1.05 |
| p5 | 11.82 | 1.67 |
| p6 | 10.54 | 1.2 |
这次分类的结果就是(p1,p2,p3),(p4,p5,p6).和上次迭代的结果是一样的,那么我们就认为可以停止迭代了最终结果就是分成这两类。
参考资料:
《机器学习基础从入门到求职》
https://www.jianshu.com/p/fc91fed8c77b





 本文详细介绍了KMeans聚类算法的过程,包括选择初始中心点、计算样本点到聚类中心的距离、更新聚类中心等步骤,并通过一个实例展示了算法的迭代过程。此外,还提到了K值选择、距离度量和损失函数等关键概念,帮助理解KMeans的工作原理。
本文详细介绍了KMeans聚类算法的过程,包括选择初始中心点、计算样本点到聚类中心的距离、更新聚类中心等步骤,并通过一个实例展示了算法的迭代过程。此外,还提到了K值选择、距离度量和损失函数等关键概念,帮助理解KMeans的工作原理。
















 310
310

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








