本文详细介绍了K-means聚类算法的工作流程、优缺点、核心点以及优化策略，如K值选择、初始化、距离度量和终止条件。探讨了如何处理离散变量、空聚类以及大数据量的快速收敛方法。此外，还提到了K-means与其他算法的关联、评估方法以及在实际应用中的场景。
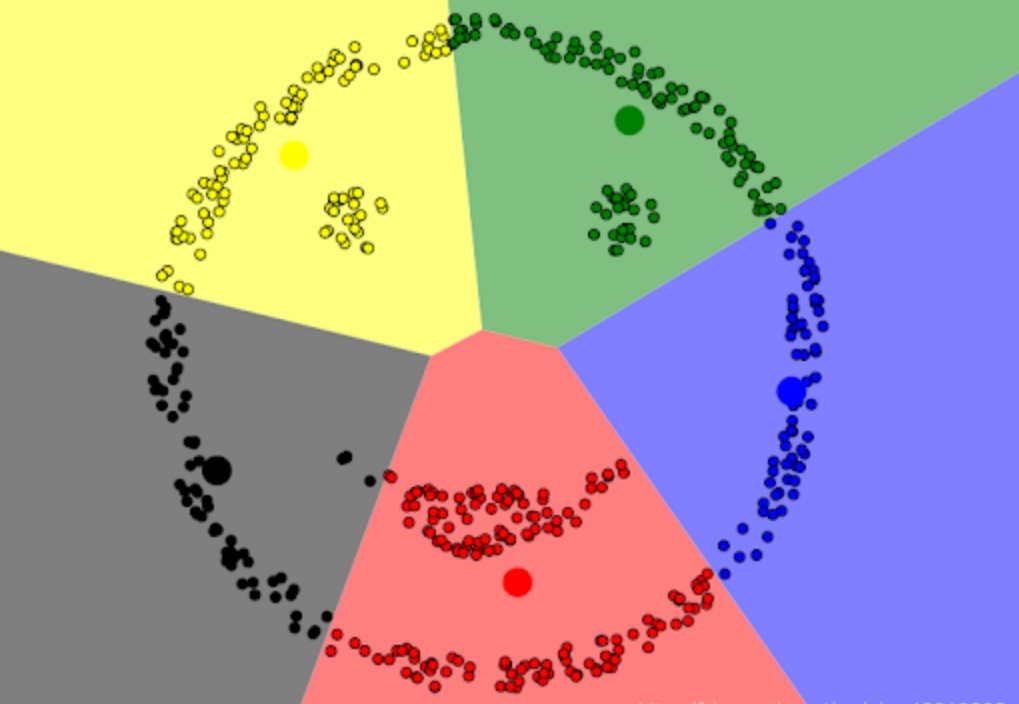
K-means
介绍完了KNN就有必要介绍一下K-means，两者还是有点相似的地方，比如都是K字辈的,比如都是基于距离的一类算法,比如核心思想里都带有臭味相投(或者近朱者赤近墨者黑)的意思。
不同的地方在于:K-means是一种聚类算法,并没有明确的标签供我们去学习,而是根据数据点之间的相似性学习到各种类别。
算法流程
- 选择初始化的K个样本作为初始聚类中心
- 针对数据集中每个样本
计算它到k个聚类中心的距离并将其分到距离最小的聚类中心所对应的类中
- 针对每个类别
,重新计算它的聚类中心
(即属于该类的所有样本的质心)
- 重复上面2,3步操作，直到达到某个终止条件(迭代次数、最小误差变化等)
复杂度分析:
- 时间复杂度:O(tkn),其中t为迭代次数，k为簇数目,n为样本点数
- 空间复杂度:O(m(n+k)),其中k为簇数目,m为样本点维度,n为样本点数
K-means的优缺点(原始的K-means)
优点:
- 容易理解，可解释性强，聚类效果也不错，尽管是局部最优
- 处理大数据的时候，该算法可以保证好的伸缩性
- 当簇近似高斯分布时，效果不错
- 算法复杂度低,接近线性(??)
- 只能收敛到局部最优 缺点:
- K需要人为设定，不同K值的解果不同
- 对初始的簇中心敏感
- 对异常值敏感
- 样本只能归为一类，不适合多分类任务
- 不太适合太离散的分类、样本类别不平衡的分类和非凸的分类
K-means的核心点
与其说是K-means的核心点，不如说是k-means可以优化的点。
从上述的算法流程中写出伪代码是容易的。但仍需关注几个点:
- K值的选择，怎样才合适？
- 随机初始化,如何才能合理？
- 距离的选择，什么数据适合用什么公式？
- 终止条件是什么
K值的选择
这里的K表示簇的数目。对于一个聚类算法而言，它本身是没有标签的，所有这个簇的选择一定要合理。
K大了,几个簇可能靠得非常近,K小了某些簇的簇内间距非常大。
如何选择呢？
- 根据对数据的简单分析可以得到。比如通过绘制数据点的图，看到可以明显区分的簇分布。或者根据一些先验知识，可以了解到数据簇数目k的合理大小
- 拐点法(手肘法):绘制一张横坐标为k，纵坐标为SSE(平方误差和)的图，它呈现的是一条弧形下降的曲线。它存在一个拐点，或者说是存在一个下降趋势不再明显的位置，该位置的k即为我们选择的K
- 轮廓系数法:计算各个类中的聚类中心到当前类中各个点的距离之平均a，再计算各个类中聚类中心到离该类最近的一个类的类中各个数据点距离之平均b。a体现簇内的内聚度，b体现与最近簇的分离度。 计算其轮廓系数:
轮廓系数的取值再-1到1之间,当簇内聚度与分度离相等时，轮廓系数为0。当b>>a时，轮廓系数近似取到1，此时模型的性能最佳。
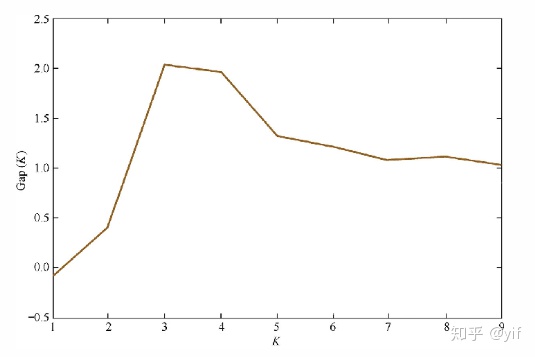
- Gap Statistic:
- 操作:在样本所在区域内按照均匀分布随机地产生和原始样本数一样多地随机样本,并对随机样本做K均值,得到
;重复多次就可以计算出
的近似。
是
的期望
- Gap(K)可以视为随机样本的损失与实际样本的损失之差
- 层次聚类:即基于合并或分裂的思想，在一定情况下停止从而获得K。
如何初始化才能更合理
K-means++诞生就是为了优化该问题。
K-means++对初始化质心做了如下优化策略：
- 从输入的数据点集合中随机选择一个点作为第一个聚类中心
- 对于数据集中的每一个点
,计算它与选择的聚类中心中最近聚类中心的距离
- 选择一个新的数据点作为新的聚类中心,选择的原则是:D(x)较大的点,被选取作为聚类中心的概率较大
- 重复2和3直到选择出k个聚类质心
- 利用这k个质心作为初始化质心去运行标准的K-means算法。
距离的选择
- 闵科夫斯基距离：定义为
该距离最常用的 p 是 2 和 1, 前者是欧几里得距离（Euclidean distance），后者是曼哈顿距离（Manhattan distance）。
闵可夫斯基距离比较直观，但是它与数据的分布无关，具有一定的局限性，如果 x 方向的幅值远远大于 y 方向的值，这个距离公式就会过度放大 x 维度的作用。 所以，在计算距离之前，我们可能还需要对数据进行 z-transform 处理，即减去均值，除以标准差：
可以看到，上述处理开始体现数据的统计特性了。这种方法在假设数据各个维度不相关的情况下利用数据分布的特性计算出不同的距离。如果维度相互之间数据相关（例如：身高较高的信息很有可能会带来体重较重的信息，因为两者是有关联的），这时候就要用到马氏距离（Mahalanobis distance）了。
- 马氏距离
马氏距离有很多优点，马氏距离不受量纲的影响，两点之间的马氏距离与原始数据的测量单位无关；由标准化数据和中心化数据(即原始数据与均值之差）计算出的二点之间的马氏距离相同。
与之前的距离不同的是它考虑到了各种特性之间的联系，并且是尺度无关的，即独立于测量尺度。
对于一个均值为
其马氏距离为
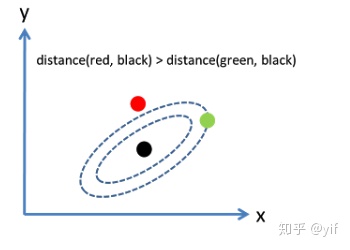
上图若是对于欧氏距离而言，红色较近，而对于马氏距离而言恰恰相反
马氏距离的变换和 PCA 分解的白化处理颇有异曲同工之妙，不同之处在于：就二维来看，PCA 是将数据主成分旋转到 x 轴（正交矩阵的酉变换），再在尺度上缩放（对角矩阵），实现尺度相同。而马氏距离的 L逆矩阵是一个下三角，先在 x 和 y 方向进行缩放，再在 y 方向进行错切（想象矩形变平行四边形），总体来说是一个没有旋转的仿射变换。
- 向量内积:本质上计算两个向量之间的夹角大小。用余弦相似度是十分常见的，
余弦相似度与向量的幅值无关，只与向量的方向相关.需要注意的是余弦相似度是受到向量的平移的影响的，比如x平移到x+1,余弦值就会改变了。
如何做到平移不变性呢?皮尔逊相关系数就具有平移不变性
皮尔逊相关系数具有平移不变性和尺度不变性。
- 汉明距离
- 1011101与1001001之间的汉明距离是2
- 2143896与2233796之间的汉明距离是3
汉明距离是指两个等长字符串s1与s2之间的汉明距离定义为将其中一个变为另一个所需要作的最小替换次数
汉明距离往往用于字符串或者二进制串中，并且一定要注意要等长的两个序列。
往往用于编码的检错纠错
- Jaccard相似度 Jaccard用于比较有限样本集之间的相似性与差异性。
- 编辑距离:是指两个字串之间由一个转成另一个所需的最少编辑次数。编辑操作包括将一个字符替换成另一个字符，插入一个字符，删除一个字符。一般来说编辑距离越小，两个串相似度越大。这里并不像汉明距离要求两个串长度一样。
终止条件
K-means的迭代终止条件有如下几种
- 每个聚类内部元素不再变化(这是最理想的情况)
- 前后两次迭代,J的值相差小于某个阈值
- 迭代超过一定次数
K-means与其他算法的关联
与K-means极其相似的是一种叫做高斯混合的模型。该模型与K-meaans不同的点在于高斯混合模型中的每个点被赋予不同的类别，并且每个类别的存在有一定的概率。而K-means针对每个数据点只分配了一个类别，如果像Soft attention和Hard Attention一样命名的化，K-means就是Hard的高斯混合模型(前者也可以叫做硬聚类，后者可以叫做软聚类)。这也就是为什么很多博文会用到EM来证明K-means的收敛性，因为在高斯混合模型中我们用的也是EM算法。
K-means的评估
因为没有标签，因此无监督学习的评估就比较特殊。
这里一般会采用以下几种评估方法:
- SSE(即用簇内误差平方和):可以比较简单的进行评估。但是因为只是针对单个簇的数据分析，而没有考虑簇与簇之间的关系，因此这种方法有一定的问题
- 轮廓系数法:没错，就是选择K值时会用到的轮廓系数,因为它既考虑了簇内的数据的关系也考虑了当前簇与其最邻近的簇的数据的关系。因此簇内簇间都考虑上了，这是很好的。
- Calinski-Harabaz Index 公式:
其中m为训练集样本数,k为类别数,
也就是说，类别内部数据的协方差越小越好，类别之间的协方差越大越好，这样的Calinski-Harabasz分数会高。
该方法相比于轮廓系数法最大的优势就是快。
K-means的一些其他点
K-means 如何处理离散变量？
标准的K-means算法不能直接应用于类别数据。类别数据的样本空间是离散的，并且没有自然来源。在这样的空间上的欧几里得距离函数并不是真正有意义的。
这时有几种解决方案:
- K-modes:这是一种基于K-means在分类特征上改良的聚类算法。与一般的K-means非常相似。
- 相同点:在算法开始前会自己设定K，然后自己设定K个初始中心点，所有样本点都被聚类到离自己最近的那个中心点;根据每个聚类，重新计算中心点，所有样本点再重新被聚类。如此反复，直到每个样本点的归属不再改变或者达到某个预设的收敛条件。
- 不同点：K-means是用每个聚类中的均值做中心点，K-modes是用每个聚类中的众数(mode)做中心点.距离的定义也不同，K-means较多使用欧氏距离，K-modes一般用汉明距离，也就是对于每个特征来说不同记为1，相同记为0
- K-prototypes:这是一种处理混合属性聚类的典型算法。继承了K-means和K-modes算法的思想。并且加入了描述数据簇的原型和混合属性数据之间相异度计算公式。
- 常规定义:
表示数据集(含有n个数据),其中数据有m个属性。
- 数据
。
表示属性j，
表示属性j的值域:对于数值属性，值域
表示的是取值范围;对于分类属性,值域
表示集合。
- 同样数据
可以表示为:
- 数据总共有m个属性，不妨设前p个属性为数值属性(r代表)，后m-r个属性为分类属性（c代表） 则有:
K-prototype算法是设定了一个目标函数，类似于kmean的SSE（误差平方和），不断迭代，直到目标函数值不变。
同时，K-prototype算法提出了混合属性簇的原型，我们可以理解原型就是数值属性聚类的质心。混合属性中存在数值属性和分类属性，其原型的定义是数值属性原型用属性中所有属性取值值的均值，分类属性原型是分类属性中选取属性值取值频率最高的属性。合起来就是原型。
相异度距离: 一般来说，数值属性的相异度一般选用欧式距离，在K-prototype算法中混合属性的相异度分为属性属性和分类属性分开求，然后相加。对于分类属性：我们使用海明威距离，即属性值相同，为0 ；属性值不同，为1。
综上，数据和簇的相异度为:
其中前p个是数值属性,后m个是分类属性，
K-prototype的目标函数是:
可以看出整个流程与K-means和K-modes并无什么区别，主要就是对数值特征和类别特征的处理特殊了点。
K-means中空聚类的处理
如果所有的点在指派步骤都未分配到某个簇，就会得到空簇。如果这种情况发生，则需要某种策略来选择一个替补质心，否则的话，平方误差将会偏大。
方法1：选择一个距离当前任何质心最远的点。这将消除当前对总平方误差影响最大的点。
方法2:从具有最大SEE的簇中选择一个替补的质心。这将分裂簇并降低聚类的总SEE。
如果有多个空簇，则该过程重复多次。
如何快速收敛数据量超大的K-means？
这时要用的是一种叫Mini-Batch K-Means的算法。
Mini Batch KMeans使用了一个种叫做 Mini Batch（分批处理）的方法对数据点之间的距离进行计算 。Mini Batch的好处是计算过程中不必使用所有的数据样本，而是从不同类别的样本中抽取一部分样本来代表各自类型进行计算。由于计算样本量少，所以会相应的减少运行时间，但另一方面抽样也必然会带来准确度的下降。 (显然这种思路不仅仅针对K-means,还被广泛应用于梯度下降等地方)
该算法的迭代步骤有两步：
1）从数据集中 随机抽取一些数据形成小批量，把他们分配给最近的质心
2）更新质心：与k均值算法相比，数据的更新是在每一个小的样本集上。对于每一个小批量，通过计算平均值得到更新质心，并把小批量里的数据分配给该质心 ，随着迭代次数的增加，这些质心的变化是逐渐减小的，直到质心稳定或者达到指定的迭代次数，停止计算。
小实践
手写K-means
这里只是简单的实现K-means，并没有包括，如何选择K值，如何评估等。Just for fun!
import numpy as np
import matplotlib.pyplot as plt
##数据生成
data1=np.random.uniform(0,2,(10,2))
data2=np.random.uniform(3,6,(10,2))
data3=np.random.uniform(8,10,(10,2))
X=np.r_[data1,data2,data3]
##模型定义
class K_means:
def __init__(self,k):
self.k=k
def distance(self,x1,x2):
return np.sqrt(np.sum(np.square(x1-x2)))
def fit(self,data):
K=np.random.uniform(0,1,(self.k,data.shape[1]))
res=np.zeros([data.shape[0],2])
count=1
while True:
K_temp_sum=np.zeros([self.k,data.shape[1]])
Count=np.zeros([self.k,1])
for i in range(data.shape[0]):
min_index=-1
mindis=np.inf
for j in range(self.k):
dis=self.distance(data[i],K[j])
if dis<mindis:
mindis=dis
min_index=j
res[i][0]=min_index
res[i][1]=mindis
K_temp_sum[min_index]=K_temp_sum[min_index]+data[i]
Count[min_index][0]+=1
for i in range(len(Count)):
if Count[i][0]==0:
Count[i][0]=np.inf
K_temp=K_temp_sum/Count
if (abs(K_temp-K)).sum()<1e-3:
K=K_temp
break
else:
K=K_temp
print("各个数据所属簇以及其距离",res)
print("各个簇类中心",K)
plt.scatter(X[:,0],X[:,1],marker='o')
plt.scatter(K[:,0],K[:,1],marker='x',color='r')
plt.show()
self.K_center=K
self.res=res
model=K_means(3)
model.fit(X)sklearn实现K-means
from sklearn.cluster import KMeans
km_cluster = KMeans(n_clusters=3, max_iter=300, n_init=40,init='k-means++',n_jobs=-1)
result = km_cluster.fit_predict(X)可以看到sklearn的还是很不错的，里面已经内置了初始值的选择算法。当然不止这些，具体的可以上网百度
应用
K-means由于简单有效被大量的用于数据预处理、数据分析等。 ##总结 网上看到的一条梳理出来的K-Means算法发展过程的轨迹.(https://zhuanlan.zhihu.com/p/25032944)
- K-means算法的提出
- 对K-means算法的性质进行分析的文章相继发出
- 对K-means算法思想进行扩展：
- a)有作者提出“Maximum Entropy”算法，并表示K-means为其一种特殊形式
- b)后又有作者提出“Mean Shift”算法，并表示“Maximum Entropy”也是其特殊形式
- 针对K-means缺陷，对K-means算法进行修改（一般仅适用于某场景）：
- a)提出online的K-means
- b)提出针对非凸数据集的K-means
- c)提出应用在FPGA中的K-means
- d)提出自动对特征进行加权的K-means
- e)Intelligent K-means算法使用异常检测的思想聚类
- 对K-means算法进行优化：
- a)KD树加速的K-means
- b)利用SVD分解加速K-means
- c)K-means++的初始化聚类中心算法
- 将K-means与新提出的思想融合：
- a)结合Ensembling与K-means
个人认为已经很全了，望补充！！
扫一扫
5651
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
