Dijkstra算法实现（JAVA）

DIjkstra算法介绍
迪杰斯特拉算法(Dijkstra)是由荷兰计算机科学家狄克斯特拉于1959 年提出的，因此又叫狄克斯特拉算法。是从一个顶点到其余各顶点的最短路径算法，解决的是有权图中最短路径问题。迪杰斯特拉算法主要特点是从起始点开始，采用贪心算法的策略，每次遍历到始点距离最近且未访问过的顶点的邻接节点，直到扩展到终点为止。
DIjkstra算法思想
算法开始选择一个顶点s作为开始节点。d表示各个节点距s的距离，p表示路径。Dijkstra算法按阶段进行，正像无权最短路径算法一样。在每个阶段，Dijkstra选择一个顶点v，他在所有的unknown的顶点中具有最小的dv，同时算法声明从s到v的最短路径known。其余阶段则更新由v已知而造成的距离变化。
下面通过一个例子说明
首先给出一张赋权图

我们将A作为开始节点S。实现代码如下：

import java.util.ArrayList;
import java.util.Arrays;


public class Graph {
    public static void main(String[] args) {
        project01.Graph graph = new project01.Graph(5);
        graph.addVertax("A");
        graph.addVertax("B");
        graph.addVertax("C");
        graph.addVertax("D");
        graph.addVertax("E");


        graph.addEdges(0,1,10);
        graph.addEdges(0,2,2);
        graph.addEdges(2,1,1);
        graph.addEdges(2,4,7);
        graph.addEdges(1,4,1);
        graph.addEdges(4,3,3);

        showEdges();
        graph.dijkStra(0);



    }
    //这里是定点数n,顶点集合Vertax，边的集合edges,是否被访问过得标记符isvisited
    private int n;
    private int numberOfEdges;
    private double[] distance;
    private String[] path;
    private ArrayList<String> Vertax;
    private static int[][] edges;
    private boolean[] isVisited;
    public  Graph(int n){
        this.n = n;
        numberOfEdges=0;
        Vertax = new ArrayList<>(n);
        edges  = new int[n][n];
        isVisited = new boolean[n+1];
        distance = new double[n];
        for (int i = 0; i <n ; i++) {
            distance[i] = Double.POSITIVE_INFINITY;
        }

        path = new String[n];
        for (int i = 0; i <n ; i++) {
            path[i] = "";
        }
    }

    //打印邻接表
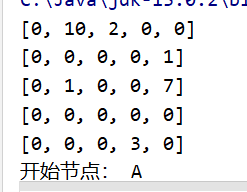
    public static void showEdges(){
        for (int[] edse: edges
        ) {
            System.out.println(Arrays.toString(edse));
        }

    }
    //获取顶点数
    public  int GetSizeOfGraph(ArrayList<String> Vertax){
        return Vertax.size();
    }
    //添加顶点
    public  void addVertax(String s){
        Vertax.add(s);
    }
    //获取指定顶点的第一个相邻顶点
    public int getFirstCO(int index){
        for (int i = 0; i <Vertax.size() ; i++) {
            if (edges[index][i]>0) return i;
        }
        return n;
    }
    //获取指定顶点的顺次相邻顶点
    public int getNextCO(int index,int firstCO){
        for (int i =firstCO+1 ; i <Vertax.size() ; i++) {
            if (edges[index][i]>0) return i;
        }
        return n;
    }
    //添加边
    public  void addEdges(int e1,int e2 , int weight){
        edges[e1][e2] = weight;
        //edges[e2][e1] = weight;
        numberOfEdges++;
    }
    //获取边数
    public int getNumberOfEdges(){
        return numberOfEdges;
    }

    public void dijkStra(int index ){

        //CO 是迭代所需坐标，headIndex为每次DIJKSTRA的启动顶点


        int CO;
        int headIndex = index;
        //
        //为初始点设置距初始点距离，自然为0
        distance[index]=0;


        //之后为每个顶点做如下操作
        //1.设置本顶点为known，本点的距离和路径不用管，因为之前已经设计好
        //2.寻找本顶点的每个相邻顶点。对于unknown的顶点，比较沿本顶点到达的距离和其原本距离，若小于原本距离，则更新距离，更新路径
        //3.本顶点设置结束后，通过indexGet函数，找出当前unknown顶点中距离最小的顶点，将其作为下一个顶点执行步骤2

        while (!isVisited[headIndex]){

            //CO为第一个没被visited的CO
            CO = getFirstCO(headIndex);
            while(isVisited[CO]){
                CO = getNextCO(headIndex,CO);
            }

            //如果headIndex顶点没有未被访问过的相邻顶点，则获得顶点坐标为n，说明他是最后一个unknown节点，仅仅需要设置为known即可
            if (CO==n) {
                isVisited[headIndex]=true;
                //System.out.println("没找到坐标");
            }
            //通过循环将所有相邻顶点执行步骤2
            else {
                while (!isVisited[CO]&&CO<n) {
                    isVisited[headIndex]=true;
                    double currentDis = distance[headIndex]+edges[headIndex][CO];
                    if (currentDis<distance[CO]) {
                        distance[CO] = currentDis;

                        path[CO] = path[headIndex]+" "+Vertax.get(headIndex);
                    }

                    CO = getNextCO(headIndex, CO);

                }
            }

            headIndex = indexGet(distance,isVisited);


        }
        for (int i = 0; i <n ; i++) {
            path[i] = path[i]+" "+Vertax.get(i);
        }
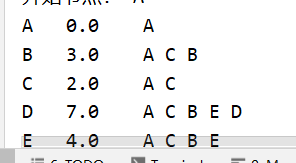
        System.out.println("开始节点： "+Vertax.get(index));
        for (int i = 0; i <n ; i++) {
            System.out.println(Vertax.get(i)+"   "+distance[i]+"   "+path[i]);
        }


    }
    //通过给定距离矩阵和访问矩阵，返回下一个需要的顶点
    public int indexGet(double[] distance, boolean[] isVisited){
        int j=0;
        double mindis=Double.POSITIVE_INFINITY;
        for (int i = 0; i < distance.length; i++) {
            if (!isVisited[i]){
                if(distance[i]<mindis){
                    mindis=distance[i];
                    j=i;
                }
            }
        }
        return j;
    }
}

最终结果如下：