-
巴什博弈
 必胜策略,第一回合消去余数,此后每次保持两个人轮流取一回合的石子数量维持在
必胜策略,第一回合消去余数,此后每次保持两个人轮流取一回合的石子数量维持在
#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
int n,m;
int main()
{
scanf("%d%d",&n,&m);
if(n%(m+1)) printf("Second");
else printf("First");
return 0;
}
-
威佐夫博弈




补充解释一下:我们可以保证,所有的数都会在奇异局势中出现一次,因此不是在
位置就是在
位置,而且性质就是
分析我们会发现,每种奇异局势的第一个值总是等于当前局势的差值乘上1.618
我们都知道0.618是黄金分割率。而威佐夫博弈正好是1.618,妙蛙

板子背景:第一堆有个石子,第二堆有
个石子,其余同上:
#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
int main()
{
int n,m;
scanf("%d%d",&n,&m);
if(n>m) swap(n,m);
//sqrt(5.0)可应用于精度较高的题目
if(floor((1+sqrt(5))/2*(m-n))==n) printf("Second");
else printf("First");
return 0;
}
-
必胜必败局面搜索
-



通常必败点和必胜点均能搜索得到,因为双方策略都是最优的
-
SG函数
- 组合博弈游戏




 Nim的板子:
Nim的板子:
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<iomanip>
#include<cmath>
#include<string>
#include<queue>
#include<set>
using namespace std;
const int mod=1e9+7;
const int maxn=100005;
#define fabs(x) x>0?x:-x
inline int read()
{
int x=0,y=1; char c=getchar();
while(c<'0'||c>'9') {if(c=='-') y=-1; c=getchar();}
while(c>='0'&&c<='9') x=x*10+c-'0',c=getchar();
return x*y;
}
int a[maxn],n;
int sum=0;
int main()
{
n=read();
for(int i=1;i<=n;i++)
{
a[i]=read();
if(!sum) sum=a[i];
else sum^=a[i];
}
if(sum!=0) printf("1");
else printf("2");
return 0;
}

-
树上和图上博弈


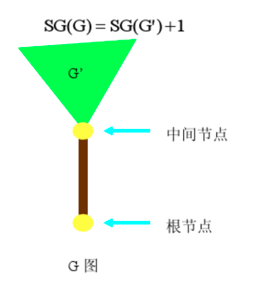




因此,图变为了树,可用树上删边博弈来完成
无向图





 本文介绍了博弈论的基础知识,包括巴什博弈的必胜策略,解释了威佐夫博弈中奇异局势与黄金分割率的联系。通过分析不同局势,揭示了博弈的胜负规律,如SG函数在组合博弈中的应用,并探讨了如何将图上的博弈转化为树上博弈进行求解。
本文介绍了博弈论的基础知识,包括巴什博弈的必胜策略,解释了威佐夫博弈中奇异局势与黄金分割率的联系。通过分析不同局势,揭示了博弈的胜负规律,如SG函数在组合博弈中的应用,并探讨了如何将图上的博弈转化为树上博弈进行求解。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








