一般情形的D-H参数
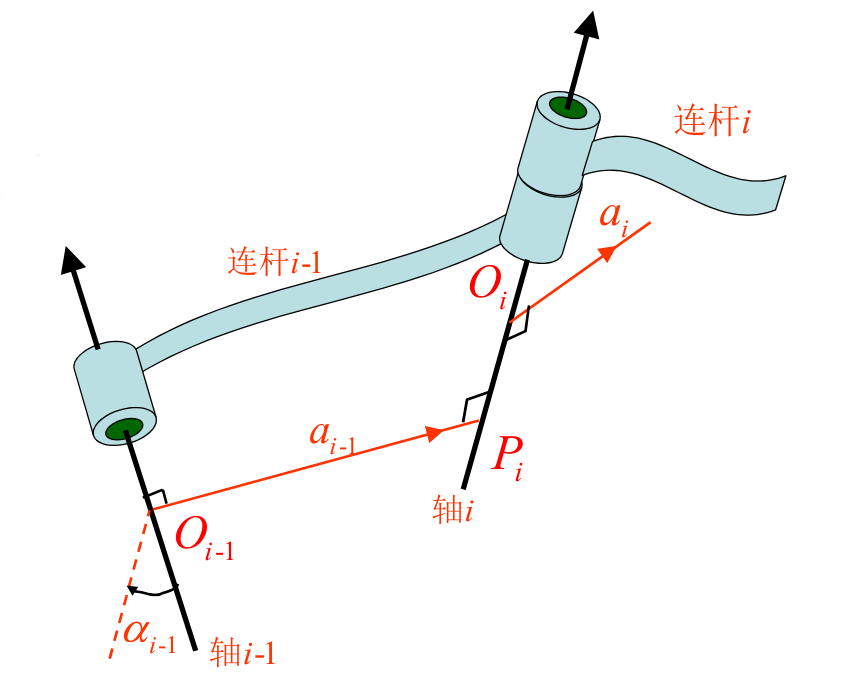
对于关节 i i i而言,其连杆参数由以下决定:
- 关节
i
−
1
i-1
i−1和关节
i
i
i间:
- 连杆长度 a i − 1 a_{i-1} ai−1:上一关节 i − 1 i-1 i−1到当前关节 i i i的公垂线距离;
- 连杆转角 α i − 1 \alpha_{i-1} αi−1:上一关节 i − 1 i-1 i−1旋转到当前关节 i i i需绕 X ^ i − 1 \hat{X}_{i-1} X^i−1旋转的角度(右手螺旋定则);
- 几何连杆
i
−
1
i-1
i−1和几何连杆
i
i
i间:
- 连杆偏距 d i d_i di:上一连杆 i − 1 i-1 i−1到下一连杆 i i i需沿 Z ^ i \hat{Z}_i Z^i平移的距离;
- 关节角 θ i \theta_i θi:上一连杆 i − 1 i-1 i−1旋转到下一连杆 i i i需绕 Z ^ i \hat{Z}_i Z^i旋转的距离(右手螺旋定则);
特殊情况:当关节 i − 1 i-1 i−1和关节 i i i处于同一平面内且非平行时,两关节间连杆长度为0
以某六自由度机械臂为例
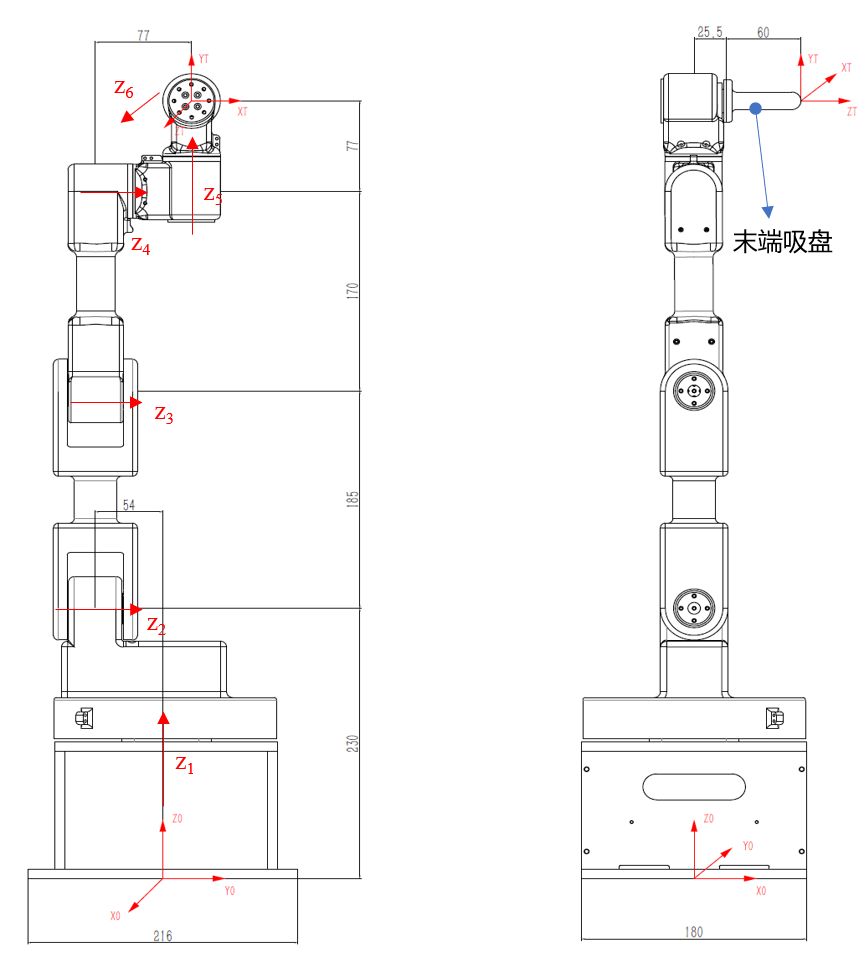
关节 Z 1 Z_1 Z1到 Z 2 Z_2 Z2、 Z 4 Z_4 Z4到 Z 5 Z_5 Z5、 Z 5 Z_5 Z5到 Z 6 Z_6 Z6都属于上述特殊情况,导致几何连杆 L 1 L_1 L1、 L 4 L_4 L4和 L 5 L_5 L5的方向(即 X ^ 1 \hat{X}_1 X^1等)无法确定,连杆转角和连杆偏距无法确定。
动态变换理解D-H参数
关节 i i i的连杆参数可以理解为关节前几何连杆 i − 1 i-1 i−1的联体坐标系 { i − 1 } \{i-1\} {i−1}需要依次经过以下变换得到关节后几何连杆 i i i的联体坐标系 { i } \{i\} {i}:
-
沿联体 X ^ \hat{X} X^滑动 a i − 1 a_{i-1} ai−1;
-
绕联体 X ^ \hat{X} X^转动 α i \alpha_i αi;
此步是将 Z ^ i − 1 \hat{Z}_{i-1} Z^i−1与 Z ^ i \hat{Z}_i Z^i对齐
-
沿联体 Z ^ \hat{Z} Z^滑动 d i − 1 d_{i-1} di−1;
-
绕联体 Z ^ \hat{Z} Z^转动 θ i \theta_i θi;
此步是将 X ^ i − 1 \hat{X}_{i-1} X^i−1和 X ^ i \hat{X}_{i} X^i对齐
对于关节 Z 1 Z_1 Z1、 Z 2 Z_2 Z2的连杆参数, { 0 } \{0\} {0}到 { 1 } \{1\} {1}无显性约束,但 { 1 } \{1\} {1}到 { 2 } \{2\} {2}较为特殊,需保证绕联体 X ^ 1 \hat{X}_{1} X^1转动后使 Z ^ 1 \hat{Z}_{1} Z^1与 Z ^ 2 \hat{Z}_2 Z^2对齐,于是 { 1 } \{1\} {1}的坐标原点 O R G 1 ORG_1 ORG1选择在 Z ^ 1 \hat{Z}_{1} Z^1与 Z ^ 2 \hat{Z}_2 Z^2的交点,且 X ^ 1 \hat{X}_{1} X^1需与二者均垂直; { 0 } \{0\} {0}到 { 1 } \{1\} {1}沿 Z ^ 0 \hat{Z}_0 Z^0移动的距离即连杆偏距 d 1 d_1 d1确定为 230 230 230, { 1 } \{1\} {1}到 { 2 } \{2\} {2}绕 Z ^ 1 \hat{Z}_1 Z^1旋转的角度即连杆转角 α 1 \alpha_1 α1为 − π / 2 -\pi/2 −π/2; Z ^ 1 \hat{Z}_{1} Z^1与 Z ^ 2 \hat{Z}_2 Z^2对齐后,考虑几何连杆本身偏距, X ^ 2 \hat{X}_2 X^2为正常情况,由 Z 2 Z_2 Z2指向 Z 3 Z_3 Z3, X ^ 1 \hat{X}_1 X^1需沿 Z ^ 1 \hat{Z}_1 Z^1平移距离 d 2 = − 54 d_2=-54 d2=−54完成和 X ^ 3 \hat{X}_3 X^3的对齐。
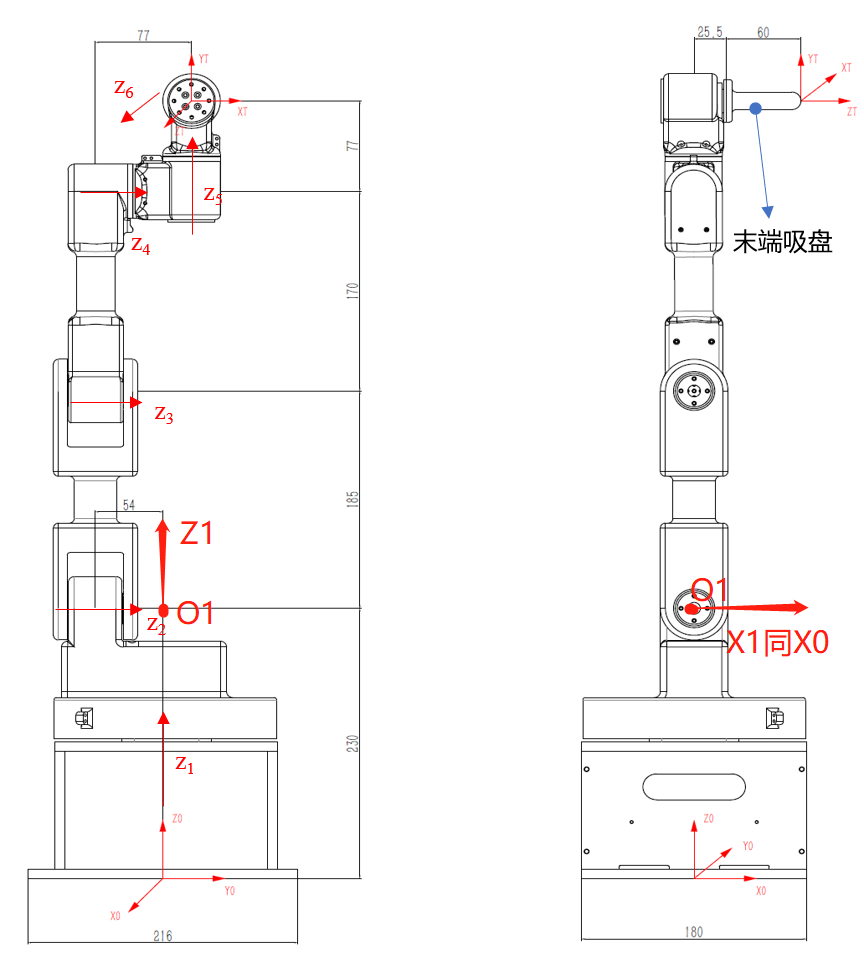
使用该方法得到最终的D-H参数:
| 关节 | α i \alpha_i αi | a i − 1 a_{i-1} ai−1 | d i d_i di | θ i \theta_i θi |
|---|---|---|---|---|
| 1 | 0 0 0 | 0 0 0 | 230 230 230 | θ 1 \theta_1 θ1 |
| 2 | − π / 2 -\pi/2 −π/2 | 0 0 0 | − 54 -54 −54 | θ 2 − π / 2 \theta_2-\pi/2 θ2−π/2 |
| 3 | 0 0 0 | 185 185 185 | 0 0 0 | θ 3 \theta_3 θ3 |
| 4 | 0 0 0 | 170 170 170 | 77 77 77 | θ 4 − π / 2 \theta_4-\pi/2 θ4−π/2 |
| 5 | − π / 2 -\pi/2 −π/2 | 0 0 0 | 77 77 77 | θ 5 − π / 2 \theta_5-\pi/2 θ5−π/2 |
| 6 | π / 2 \pi/2 π/2 | 0 0 0 | 85.5 85.5 85.5 | θ 6 \theta_6 θ6 |
关节角 θ i \theta_i θi的偏置需要由机械臂的初始状态决定。























 345
345

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








