C语言--算法篇（1）（点灯笼）二叉树（下）

于 2019-04-23 16:19:05 发布
阅读量273 收藏
点赞数
CC 4.0 BY-SA版权
分类专栏： C语言-基础 C语言-算法
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/zjc910997316/article/details/89473552
本文详细介绍了二叉搜索树的构建过程，包括插入节点、先序、中序及后序遍历，以及如何求树的高度和最大值。通过具体代码示例，展示了二叉搜索树的基本操作。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

 

 

1 二叉搜索树：

binary search tree 二叉搜索树：
简写：BST
要求：左<根<右
对于二叉搜索树最大值在最右边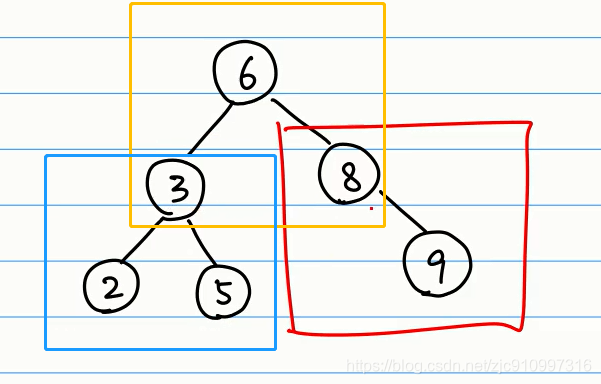

构件树

下面是构件树过程：

下面序列，一次放入数，小的放左边，大的放右边

6 3 8 2 5 1 7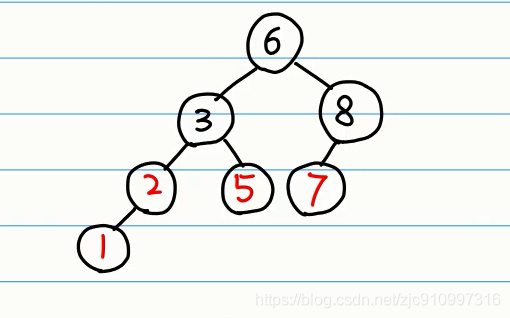

2 整体打包:

只需要知道根节点就知道树的整体了

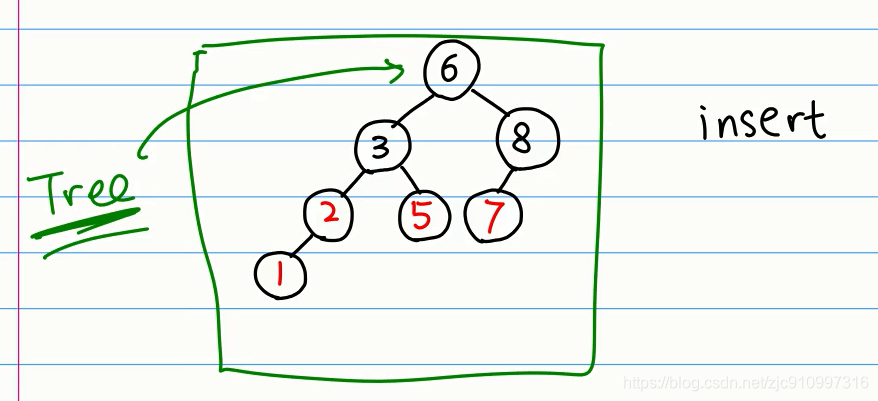
先序遍历结果：6321587

中序遍历结果：1235678

 

生成树，通过先序遍历验证：

#include<stdio.h>
#include<windows.h>
#include<string.h>
#include<stdlib.h>  // 因为需要写NULL，所以需要这个库
#include<malloc.h>  // 这里用于申请内存
//本代码建立在<没有重复数字>的前提下

// 节点结构体
typedef struct node {
	int data;
	struct node* left;
	struct node* right;
} Node;

// 构建树结构体
typedef struct {
	Node* root;
} Tree;

// 插入
void insert (Tree* tree, int value) {
	Node* node = (Node* )malloc( sizeof(Node) );  // 申请内存，这样在结束之后不会被销毁掉
	node -> data = value;
	node -> left = NULL;
	node -> right = NULL;

	if (tree -> root == NULL) {  // 如果一开始没有根节点，那就直接写入根节点
		tree -> root = node;
	}
	else {
		Node* temp = tree ->root;
		while (temp != NULL) {
			if (value < temp -> data) {
				if (temp ->left == NULL) {
					temp -> left = node;
					return ;
				}
				else {
					temp = temp -> left;
				}
			}
			else {
				if (temp -> right == NULL) {
					temp -> right = node;
					return ;
				}
				else {
					temp = temp -> right;
				}
			}
		}
	}
}

// 先序遍历, 在这里node是一个指针
void preorder(Node* node) {  
	if (node != NULL) {
		printf("%d\n", node -> data);  // 在这里node是一个指针,因而使用->
		preorder(node -> left);
		preorder(node -> right);
	}
}

// 中序遍历, 在这里node是一个指针
void inorder(Node* node) {  
	if (node != NULL) {		
		inorder(node -> left);
		printf("%d\n", node -> data);  // 在这里node是一个指针,因而使用->
		inorder(node -> right);
	}
}

// 后序遍历, 在这里node是一个指针
void postorder(Node* node) {  
	if (node != NULL) {		
		postorder(node -> left);
		postorder(node -> right);
		printf("%d\n", node -> data);  // 在这里node是一个指针,因而使用->
	}
}

int main() {
	int arr[7] = {6, 3, 8, 2, 5, 1, 7};
	Tree tree;
	int i;
	tree.root = NULL;

	
	for (i=0; i<7; i++) {
		insert(&tree, arr[i]);
	}

	preorder(tree.root);  // 暂时还不明白为什么这里没有&tree.root？？？
    // 通常检查一棵树是否是对的，通过检查先序遍历&中序遍历

	Sleep(10000);
}

先序遍历结果：

3 生成树，通过中序遍历验证：

我们会发现中序遍历正好是从小到大排序的结果，因为我们的树就是按照这个规则建立的。

#include<stdio.h>
#include<windows.h>
#include<string.h>
#include<stdlib.h>  // 因为需要写NULL，所以需要这个库
#include<malloc.h>  // 这里用于申请内存
//本代码建立在<没有重复数字>的前提下

// 节点结构体
typedef struct node {
	int data;
	struct node* left;
	struct node* right;
} Node;

// 构建树结构体
typedef struct {
	Node* root;
} Tree;

// 插入
void insert (Tree* tree, int value) {
	Node* node = (Node* )malloc( sizeof(Node) );  // 申请内存，这样在结束之后不会被销毁掉
	node -> data = value;
	node -> left = NULL;
	node -> right = NULL;

	if (tree -> root == NULL) {  // 如果一开始没有根节点，那就直接写入根节点
		tree -> root = node;
	}
	else {
		Node* temp = tree ->root;
		while (temp != NULL) {
			if (value < temp -> data) {
				if (temp ->left == NULL) {
					temp -> left = node;
					return ;
				}
				else {
					temp = temp -> left;
				}
			}
			else {
				if (temp -> right == NULL) {
					temp -> right = node;
					return ;
				}
				else {
					temp = temp -> right;
				}
			}
		}
	}
}

// 先序遍历, 在这里node是一个指针
void preorder(Node* node) {  
	if (node != NULL) {
		printf("%d\n", node -> data);  // 在这里node是一个指针,因而使用->
		preorder(node -> left);
		preorder(node -> right);
	}
}

// 中序遍历, 在这里node是一个指针
void inorder(Node* node) {  
	if (node != NULL) {		
		inorder(node -> left);
		printf("%d\n", node -> data);  // 在这里node是一个指针,因而使用->
		inorder(node -> right);
	}
}

// 后序遍历, 在这里node是一个指针
void postorder(Node* node) {  
	if (node != NULL) {		
		postorder(node -> left);
		postorder(node -> right);
		printf("%d\n", node -> data);  // 在这里node是一个指针,因而使用->
	}
}

int main() {
	int arr[7] = {6, 3, 8, 2, 5, 1, 7};
	Tree tree;
	int i;
	tree.root = NULL;

	
	for (i=0; i<7; i++) {
		insert(&tree, arr[i]);
	}

	inorder(tree.root);  // 通常检查一棵树是否是对的，通过检查先序遍历&中序遍历

	Sleep(10000);
}

中序遍历结果：

我们会发现中序遍历正好是从小到大排序的结果，因为我们的树就是按照这个规则建立的。

简单吧~

4 求树的高度：需要用到递归

关于递归，请参考我的另外的博文：
C语言--（六）递归Recursion（点灯笼）
https://blog.youkuaiyun.com/zjc910997316/article/details/88983773

 

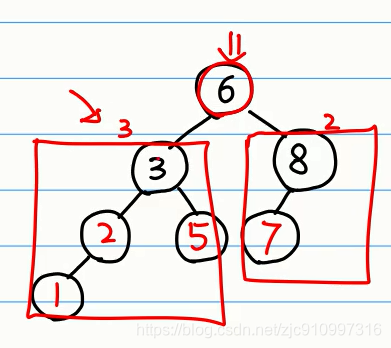
此树高度是4

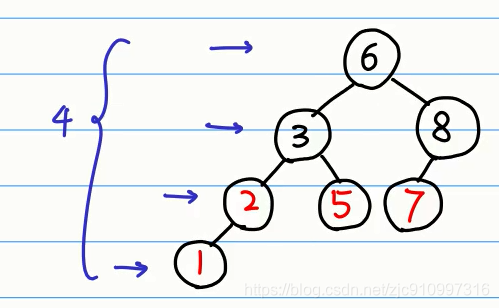
计算高度思路：

左边比较大，左孩子高度加一即可。

求树高完整代码;

#include<stdio.h>
#include<windows.h>
#include<string.h>
#include<stdlib.h>  // 因为需要写NULL，所以需要这个库
#include<malloc.h>  // 这里用于申请内存
//本代码建立在<没有重复数字>的前提下

// 节点结构体
typedef struct node {
	int data;
	struct node* left;
	struct node* right;
} Node;

// 构建树结构体
typedef struct {
	Node* root;
} Tree;

// 插入
void insert (Tree* tree, int value) {
	Node* node = (Node* )malloc( sizeof(Node) );  // 申请内存，这样在结束之后不会被销毁掉
	node -> data = value;
	node -> left = NULL;
	node -> right = NULL;

	if (tree -> root == NULL) {  // 如果一开始没有根节点，那就直接写入根节点
		tree -> root = node;
	}
	else {
		Node* temp = tree ->root;
		while (temp != NULL) {
			if (value < temp -> data) {
				if (temp ->left == NULL) {
					temp -> left = node;
					return ;
				}
				else {
					temp = temp -> left;
				}
			}
			else {
				if (temp -> right == NULL) {
					temp -> right = node;
					return ;
				}
				else {
					temp = temp -> right;
				}
			}
		}
	}
}

// 1 先序遍历, 在这里node是一个指针
void preorder(Node* node) {  
	if (node != NULL) {
		printf("%d\n", node -> data);  // 在这里node是一个指针,因而使用->
		preorder(node -> left);
		preorder(node -> right);
	}
}

// 2 中序遍历, 在这里node是一个指针
void inorder(Node* node) {  
	if (node != NULL) {		
		inorder(node -> left);
		printf("%d\n", node -> data);  // 在这里node是一个指针,因而使用->
		inorder(node -> right);
	}
}

// 3 后序遍历, 在这里node是一个指针
void postorder(Node* node) {  
	if (node != NULL) {		
		postorder(node -> left);
		postorder(node -> right);
		printf("%d\n", node -> data);  // 在这里node是一个指针,因而使用->
	}
}

// 求树高度
int get_height (Node* node) {  // 左边比较大，左孩子高度加一即是当前树的高度。
	if (node == NULL) {
		return 0;
	}
	else {
		int left_h = get_height(node -> left);
		int right_h = get_height(node -> right);
		int max = left_h;
		if (right_h > left_h) {
			max = right_h;
		}
		return max + 1;
	}
}

int main() {
	int arr[7] = {6, 3, 8, 2, 5, 1, 7};
	Tree tree;
	int i;
	int h;
	tree.root = NULL;

	
	for (i=0; i<7; i++) {
		insert(&tree, arr[i]);
	}

	// inorder(tree.root);  // 通常检查一棵树是否是对的，通过检查先序遍历&中序遍历
	h = get_height(tree.root);// 求树高度
	printf("h = %d", h);

	Sleep(10000);
}

结果：

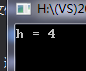
重点提示：

递归一定设置好递归出口

int get_height (Node* node) {  // 左边比较大，左孩子高度加一即是当前树的高度。
	
    if (node == NULL) {  // 这里是递归出口，当到了子节点没有东西的时候结束
		return 0;
	}
    
	else {
		int left_h = get_height(node -> left);
		int right_h = get_height(node -> right);
		int max = left_h;
		if (right_h > left_h) {
			max = right_h;
		}
		return max + 1;
	}
}

5 求最大值：

1 对于二叉搜索树最大值在最右边

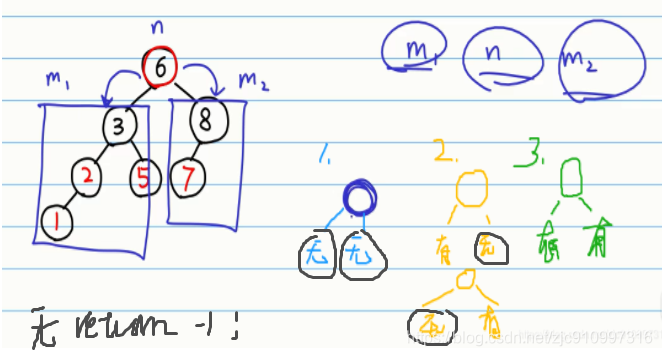
2 对于任意给定的一棵树求最大值，思路如下：

取 max(m1, m2) 与 n 比较。

求整个树中的最大值max完整代码:

#include<stdio.h>
#include<windows.h>
#include<string.h>
#include<stdlib.h>  // 因为需要写NULL，所以需要这个库
#include<malloc.h>  // 这里用于申请内存
//本代码建立在<没有重复数字>的前提下

// 节点结构体
typedef struct node {
	int data;
	struct node* left;
	struct node* right;
} Node;

// 构建树结构体
typedef struct {
	Node* root;
} Tree;

// 插入
void insert (Tree* tree, int value) {
	Node* node = (Node* )malloc( sizeof(Node) );  // 申请内存，这样在结束之后不会被销毁掉
	node -> data = value;
	node -> left = NULL;
	node -> right = NULL;

	if (tree -> root == NULL) {  // 如果一开始没有根节点，那就直接写入根节点
		tree -> root = node;
	}
	else {
		Node* temp = tree ->root;
		while (temp != NULL) {
			if (value < temp -> data) {
				if (temp ->left == NULL) {
					temp -> left = node;
					return ;
				}
				else {
					temp = temp -> left;
				}
			}
			else {
				if (temp -> right == NULL) {
					temp -> right = node;
					return ;
				}
				else {
					temp = temp -> right;
				}
			}
		}
	}
}

// 先序遍历, 在这里node是一个指针
void preorder(Node* node) {  
	if (node != NULL) {
		printf("%d\n", node -> data);  // 在这里node是一个指针,因而使用->
		preorder(node -> left);
		preorder(node -> right);
	}
}

// 中序遍历, 在这里node是一个指针
void inorder(Node* node) {  
	if (node != NULL) {		
		inorder(node -> left);
		printf("%d\n", node -> data);  // 在这里node是一个指针,因而使用->
		inorder(node -> right);
	}
}

// 后序遍历, 在这里node是一个指针
void postorder(Node* node) {  
	if (node != NULL) {		
		postorder(node -> left);
		postorder(node -> right);
		printf("%d\n", node -> data);  // 在这里node是一个指针,因而使用->
	}
}

// 计算树高
int get_height (Node* node) {  // 左边比较大，左孩子高度加一即是当前树的高度。
	if (node == NULL) {
		return 0;
	}
	else {
		int left_h = get_height(node -> left);
		int right_h = get_height(node -> right);
		int max = left_h;
		if (right_h > left_h) {
			max = right_h;
		}
		return max + 1;
	}
}

// 计算树中的最大值
int get_maximum(Node* node) {
	if (node  == NULL) {
		return -1;  // 空节点
	}
	else {
		int m1 = get_maximum(node -> left);
		int m2 = get_maximum(node -> right);
		int m3 = node ->data;
		int max = m1;
		if (m2 > max) { max = m2; }
		if (m3 > max) { max = m3; }
		return max;
	}
}

int main() {
	int arr[7] = {6, 3, 8, 2, 5, 1, 7};
	Tree tree;
	int i;
	int h;
	int m;
	tree.root = NULL;

	
	for (i=0; i<7; i++) {
		insert(&tree, arr[i]);
	}

	// inorder(tree.root);  // 通常检查一棵树是否是对的，通过检查先序遍历&中序遍历
	// h = get_height(tree.root);
	// printf("h = %d", h);

	m = get_maximum(tree.root);
	printf("maximum = %d", m);

	Sleep(10000);
}

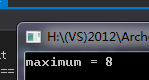
结果：

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

计算机视觉-Archer

图像分割没有团队的同学可加群

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值