DAY6 7.27

模拟赛：
A：简单恶心题。不难发现只有当两个数没有两个1在同一位时答案为1，否则为2。所以维护前面有多少个和自己1的位置完全不一样的位置，容斥即可。

B：大型分讨题。首先如果有3个或以上长度大于等于 $k$ 的串，则不合法。2个，则必须翻转这两个，判断能否即可。1个，则枚举其他所有段，看是否可以翻转即可。0个，直接结束。

C（CF1550E）：典题。二分是自然地，考虑check。容易想到一个 $O(nk{2}^k)$ 的dp，即 $f_{i,j}$ 表示以 $i$ 结尾 $j$ 的字母出现状态是否可行（其中j为$2^k$）。但是不难发现当 $f_{i,j}$ 为1时，$f_{i+k,j}$ 一定也为1。而我们 $f$ 的值记录的也很差，不妨考虑交换值与状态，这是一个常用的技巧，可以很好的减少 dp 时间复杂度。即考虑 $f_i$ 表示字母出现状态为i，可以达成该情况的最小位置 $f_i$. 那么这样时间复杂度就降到了 $O(k{2}^k)$.

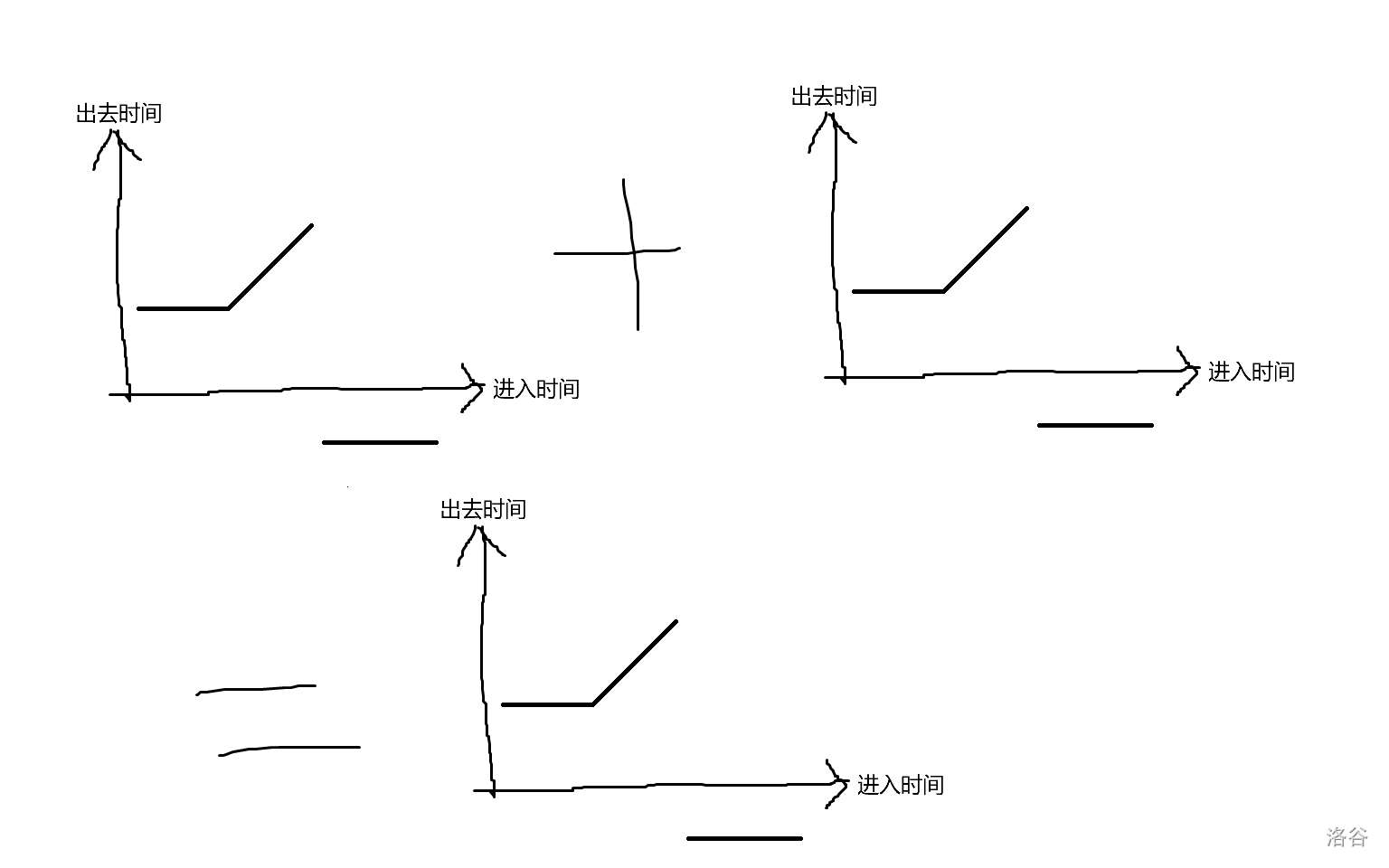
D：典题+板题。线段树维护是不难想到的。不难发现对于一个区间进入和出来的时间应该是如下的一个情况（数轴下面那段表示超时失败），而手玩后发现（甚至不用手玩，因为函数合并形状不变是必然的）下一个区间还是这样的。所以考虑维护两个转折的位置 $t_1$ 和 $t_2$，每次简单 push_up 即可。

教训：B题应该手动再去思考讨论是否完备。对于 C 题的 $k\le 17$，显然是状压 $2^k$，去思考不状压是没有前途的。D题在肯定线段树且单点修改时，应该去思考如何设置每个点表示的东西，如何push_up。