4、广度优先搜索

 

一、课程目标

了解广度优先搜索算法的原理，能够编码使用深搜的思想来解决问题。

二、目标详解

广度优先搜索算法（又称宽度优先搜索）是最简便的图的搜索算法之一，这一算法也是很多重要的图的算法的原型。Dijkstra单源最短路径算法和Prim最小生成树算法都采用了和宽度优先搜索类似的思想。其别名又叫BFS，属于一种盲目搜寻法，目的是系统地展开并检查图中的所有节点，以找寻结果。换句话说，它并不考虑结果的可能位置，彻底地搜索整张图，直到找到结果为止。

基本思想

已知图G=(V,E)和一个源顶点s，宽度优先搜索以一种系统的方式探寻G的边，从而“发现”s所能到达的所有顶点，并计算s到所有这些顶点的距离(最少边数)，该算法同时能生成一棵根为s且包括所有可达顶点的宽度优先树。对从s可达的任意顶点v，宽度优先树中从s到v的路径对应于图G中从s到v的最短路径，即包含最小边数的路径。该算法对有向图和无向图同样适用。

之所以称之为宽度优先算法，是因为算法自始至终一直通过已找到和未找到顶点之间的边界向外扩展，就是说，算法首先搜索和s距离为k的所有顶点，然后再去搜索和S距离为k+l的其他顶点。

为了保持搜索的轨迹，宽度优先搜索为每个顶点着色：白色、灰色或黑色。算法开始前所有顶点都是白色，随着搜索的进行，各顶点会逐渐变成灰色，然后成为黑色。在搜索中第一次碰到一顶点时，我们说该顶点被发现，此时该顶点变为非白色顶点。因此，灰色和黑色顶点都已被发现，但是，宽度优先搜索算法对它们加以区分以保证搜索以宽度优先的方式执行。若(u,v)∈E且顶点u为黑色，那么顶点v要么是灰色，要么是黑色，就是说，所有和黑色顶点邻接的顶点都已被发现。灰色顶点可以与一些白色顶点相邻接，它们代表着已找到和未找到顶点之间的边界。

在宽度优先搜索过程中建立了一棵宽度优先树，起始时只包含根节点，即源顶点s.在扫描已发现顶点u的邻接表的过程中每发现一个白色顶点v，该顶点v及边(u,v)就被添加到树中。在宽度优先树中，我们称结点u 是结点v的先辈或父母结点。因为一个结点至多只能被发现一次，因此它最多只能有–个父母结点。相对根结点来说祖先和后裔关系的定义和通常一样：如果u处于树中从根s到结点v的路径中，那么u称为v的祖先，v是u的后裔。

示例

下图是一张有向图，按照广搜的思路对其每个顶点做一次访问：

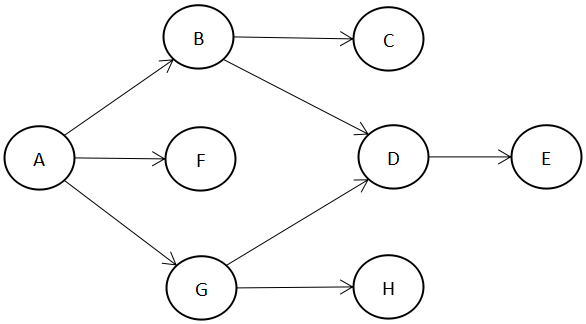
1. 顶点A入队，队列中：A。
2. 访问A，A出队，B、F、G入队，队列中：B、F、G。
3. 访问B，B出队，C、D入队，队列中：F、G、C、D。
4. 访问F，F出队，无可入队顶点，队列中：G、C、D。
5. 访问G，G出队，D已在队列中，H入队，队列中：C、D、H。
6. 访问C，C出队，无可入队顶点，队列中：D、H。
7. 访问D，D出队，E入队，队列中：H、E。
8. 访问H，H出队，无可入队顶点，队列中：E。
9. 访问E，E出队，无可入队顶点，队列空。
10. 队空，结束。

访问序列为ABFGCDHE。

可以发现，整个遍历过程是分层进行的，先遍历了距离起点为1的所有顶点，再是距离为2的顶点，···，直到所有顶点访问完毕，层次结构如下图：

使用伪代码来表示广搜的执行逻辑：

主程序
  起点入队
  while 队不为空
    队首出队并访问
    for 出队顶点相连接顶点
      队尾入队并记录

广度优先搜索是在处理图类问题时的一种搜索思路，在实际问题中，可能不需要访问所有顶点，也可能每个顶点可以访问多次，具体的代码实现应根据不同的问题情况来进行。