3、深度优先搜索

 

一、课程目标

了解深度优先搜索算法的原理，能够编码使用深搜的思想来解决问题。

二、目标详解

搜索

在编程遇到的问题中，有些问题我们不能够确切的找出数学模型，即找不出一种直接求解的方法，解决这一类问题，我们一般采用搜索的方法解决。搜索就是用问题的所有可能去试探，按照一定的顺序、规则，不断去试探，直到找到问题的解，试完了也没有找到解，那就是无解，试探时一定要试探完所有的情况（实际上就是穷举）。

搜索是人工智能中的一种基本方法，是一项非常普遍使用的算法策略，能够解决许许多多的常见问题，在某些情况下我们很难想到高效的解法时，搜索往往是可选的唯一选择。按照标准的话来讲：搜索算法是利用计算机的高性能来有目的的穷举一个问题的部分或所有的可能情况，从而求出问题的解的一种方法。

搜索虽然简单易学易于理解，但要掌握好并写出速度快效率高优化好的程序却又相当困难，总而言之，搜索算法灵活多变，一般的框架很容易写出，但合适的优化却要根据实际情况来确定。在搜索算法中，深度优先搜索（也可以称为回溯法）是搜索算法里最简单也最常见的。

深度优先搜索

深度优先搜索是一种在开发爬虫早期使用较多的方法。它的目的是要达到被搜索结构的叶结点（即那些不包含任何超链的HTML文件）。在一个HTML文件中，当一个超链被选择后，被链接的HTML文件将执行深度优先搜索，即在搜索其余的超链结果之前必须先完整地搜索单独的一条链。深度优先搜索沿着HTML文件上的超链走到不能再深入为止，然后返回到某一个HTML文件，再继续选择该HTML文件中的其他超链。当不再有其他超链可选择时，说明搜索已经结束。

事实上，深度优先搜索属于图算法的一种，英文缩写为DFS即Depth First Search，其过程简要来说是从某个顶点出发，对每一个可能的分支路径深入到不能再深入为止，然后再回溯到最近的一个分叉口选择另一条路径继续深入，直到所有节点都被访问过一次。通俗来讲就是“一直向下走，走不通就掉头。”，类似于二叉树的先序遍历。

举例说明一下，如下图是一个有向图，按照深搜的思路对其每个顶点做一次访问：

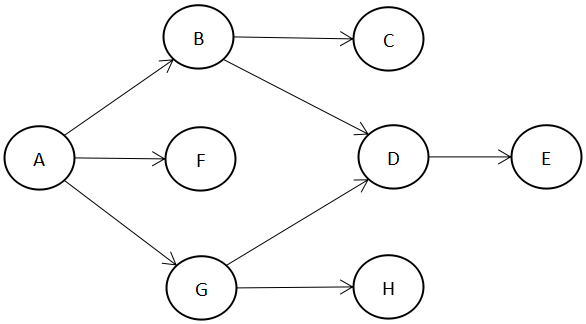
1. 访问A顶点，其指向的顶点有B、F、G。
2. 访问B顶点，其指向的顶点有C、D。
3. 访问C顶点，无指向顶点，该条路径访问结束。
4. 回溯到B顶点，指向的顶点中还剩下D没有访问。
5. 访问D顶点，其指向的顶点有E。
6. 访问E顶点，无指向顶点，该条路径访问结束。
7. 回溯到D，指向顶点均已访问，继续回溯到B，也都访问过，继续回溯到A，指向顶点中还剩F、G。
8. 访问F顶点，无指向顶点，回溯到A。
9. 访问G顶点，指向顶点有D、H，其中D已被访问。
10. 访问H顶点，结束。

得到访问序列ABCDEFGH。

可以发现，整个搜索过程是一个递归的结构，用伪代码表示出来为：

dfs(顶点)
  记录访问了顶点
  for 每个指向顶点
    if 顶点没有被访问过
      dfs(顶点)
主程序
  dfs(起始顶点)

深度优先搜索是在处理图类问题时的一种搜索思路，在实际问题中，可能不需要访问所有顶点，也可能每个顶点可以访问多次，具体的代码实现应根据不同的问题情况来进行。