红黑树的原理，双红缺陷，双黑缺陷

引入

      引入红黑树的目的是为了实现在维护BST平衡的同时，尽量控制拓扑结构调整的次数，即最好做到每次动态操作后只有O（1）次的拓扑调整。

 红黑树的规则：

（1）树根必须是黑色；

（2）外部节点必须为黑色；

（3）其余节点：红节点只能有黑孩子，即不能出现相邻的父子两代都为红色；

（4）外部节点到根：所有外部节点的黑深度相同。

       在红黑树中，提升红色节点，使之与黑父亲等高，每颗红黑树都会等价于一棵4阶的B树，也叫（2,4）树，在红黑树的动态调整中，借助于B树可以方便我们理解。

插入

调用BST的插入算法，引入一个新的末端节点，并初始化时将其染为红色。如果其父亲p也为红色时，就会发生双红缺陷。

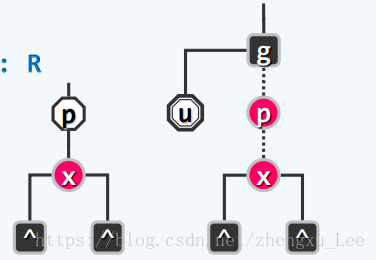
p=x->parent();//父节点
g=p->parent();//祖父节点
u=(p==g->lc)?g->rc:g->lc;//叔父节点

（1）叔父节点u为黑色时，有如下两种情况

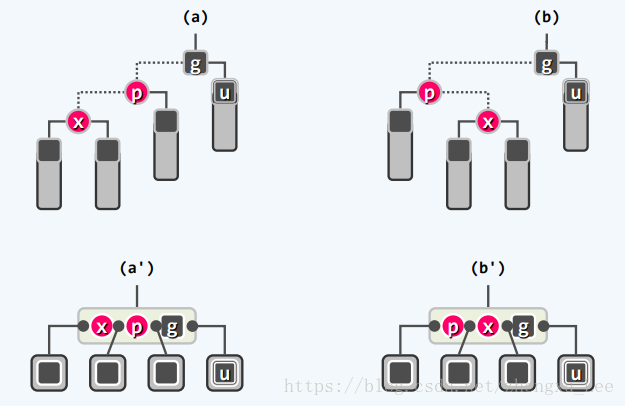
对应问题为在B树中，超级节点内有两个相邻的红色节点，可做一次3+4重构，并将中间的红色节点染为黑色，另一个相邻的黑色节点染为红色解决。