python蒙特卡洛方法求圆周率

最新推荐文章于 2024-12-18 16:33:08 发布

原创

最新推荐文章于 2024-12-18 16:33:08 发布 · 7.1k 阅读

15 ·

CC 4.0 BY-SA版权

文章标签：

#机器学习 #python

使用Python的蒙特卡洛方法，通过在单位正方形内随机生成点并计算落入1/4圆内的点的比例，进而求得圆周率π的近似值。通过对不同投点数量的实验，计算均值和方差，并展示结果。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

蒙特卡洛方法求解圆周率pi

工具

python3.7 + pycharm

求解思路

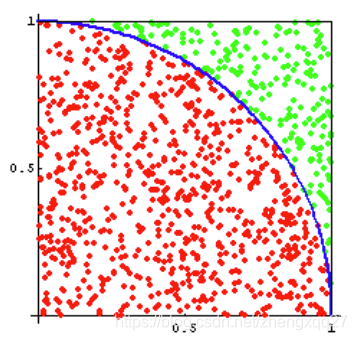
首先使用random函数随机生成单位正方形之间的点，记录其分布情况，再求出1/4圆内的点与单位正方形内点的比值，将该值乘以4即为pi值，重复上述过程20次，利用numpy.mean函数和numpy.var函数求出均值mean和方差variance。改变投点个数，记录对应的mean和variance，用PrettyTable绘制结果表格。

python源代码

1.	import random  
2.	import numpy as np  
3.	from prettytable import PrettyTable  
4.	  
5.	  
6.	def getPi():  
7.	    arr = []  
8.	    table = PrettyTable(["point num", "mean", "variance"])  
9.	    time = [20, 50, 100, 200, 300, 500, 1000, 5000]  
10.	    for t in time:  
11.	        # print(t)  
12.	        for j in range(20):  
13.	            cnt = 0  
14.	            for i in range(t):  
15.	                x = random.uniform(0, 1)  # 从一个均匀分布中随机采样，区间为左闭右开  
16.	                y = random.uniform(0, 1)  
17.	  
18.	                if