自存。PDF 下载链接
第一讲 基本的神经元模型
1)神经元模型
最简单的MP模型,右图是“与”逻辑的数学表达:
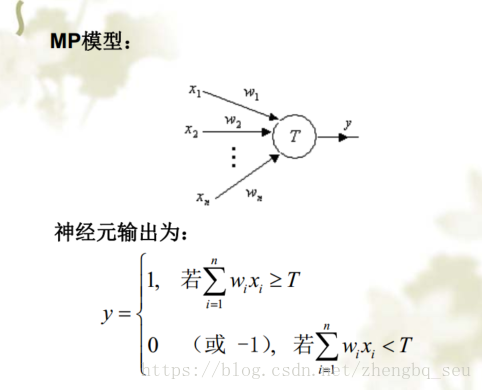
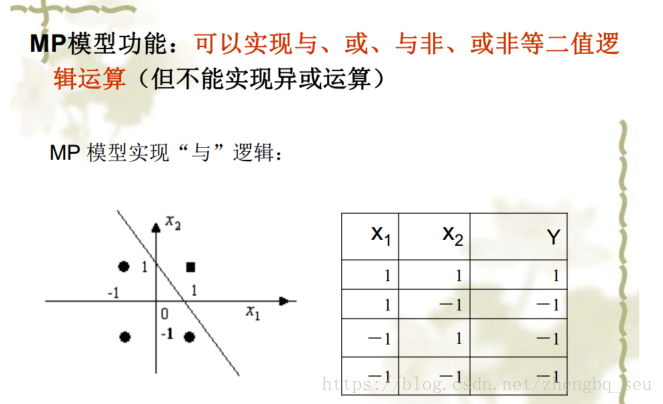
神经元模型 基函数表示“如何组合” 激活函数表示“是否到阈值”“最后网络表达的方式”
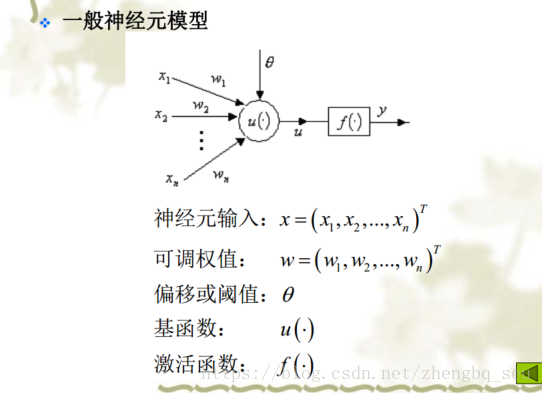
基函数类型1:线性函数 基函数类型2:距离函数


激活函数类型:1)硬极限函数(sgn,大于0为1,否则为0);2)线性函数(常用于实现函数逼近的神经网络的输出层神经元。作为隐层神经元的激活函数时,线性函数常用于理论分析);3)饱和线性函数 (饱和激活函数也常用于分类。缺点:多个饱和线性函数前后互联时,会导致神经网络系统分析困难 );4)Sigmoidal函数 (也叫 S函数,是一类非常重要的激活函数,无论神经网络用于分类、函数逼近或优化, Sigmoidal函数都是常用的激活函数。表达式1/(1+ exp(- lenta u));5)径向基函数(极为重要的一类激活函数,常用于径向基函数神经网络(RBF网络))。 (不放图了 太占地方)
2)神经元学习算法
(1)Hebb学习规则是一种无导学习算法 ,Hebb规则说明:使用频繁的突触联系会变得更紧密,从而可理解为突触的特点是用进废退。除了上基本Hebb学习规则,根据应用的不同,还有Oja和Karhunenn的非线性Hebb学习算法。Hebb学习规则常用于自组织网络或特征提取网络。![]()
(2)离散感知器学习规则: 如果神经元的基函数取线性函数,激活函数取硬极限函数,则神经元就成了单神经元感知器(离散感知器)。单神经元感知器的学习规则称离散感知器学习规则,是一种有导学习算法 。
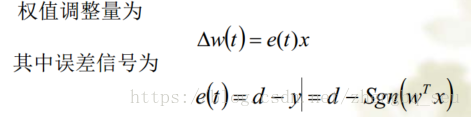
(3)δ学习规则也称梯度法或最速下降法,是最常用的神经网络学习算法。 δ学习规则是一种有导学习算法。



(4)Widrow-Hoff学习规则也是一种有导学习算法。 Widrow-Hoff学习规则常用于自适应线性单元(Adaline) 我觉得就是基函数确定为线性函数的δ学习规则而已
3)单个神经元解决问题的能力
以“异或问题”为例,

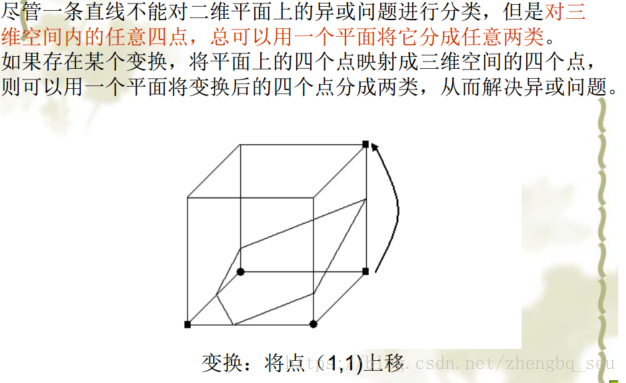








 本文介绍了神经网络的基础,包括神经元模型、学习算法和单个神经元解决问题的能力。讲解了MP模型、Hebb学习规则、BP算法以及RBF神经网络的结构、工作原理和学习算法,探讨了不同算法的优缺点。
本文介绍了神经网络的基础,包括神经元模型、学习算法和单个神经元解决问题的能力。讲解了MP模型、Hebb学习规则、BP算法以及RBF神经网络的结构、工作原理和学习算法,探讨了不同算法的优缺点。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章
















 454
454

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








