学习笔记 - GreedyAI - DeepLearningCV - Zhibo Neural-Network-Loss

第6章 神经网络损失函数（Neural Network Loss Function)

损失函数

loss=“mean_squared_error”

model.compile(loss="mean_squared_error", optimizer="sgd", metrics=["mae", "acc])

大纲

• 入门

  • 定义，特性，训练过程

• 常用损失函数

  • 回归
  • 分类

• 正则化

• 实例

入门

• 定义

在深度学习中，损失函数是用来衡量一组参数的质量的函数，衡量的方式是比较网络输出和真实输出的差异。

• 命名

损失函数（loss function）、代价函数（cost function）、目标函数（objective function）、误差函数（error function）

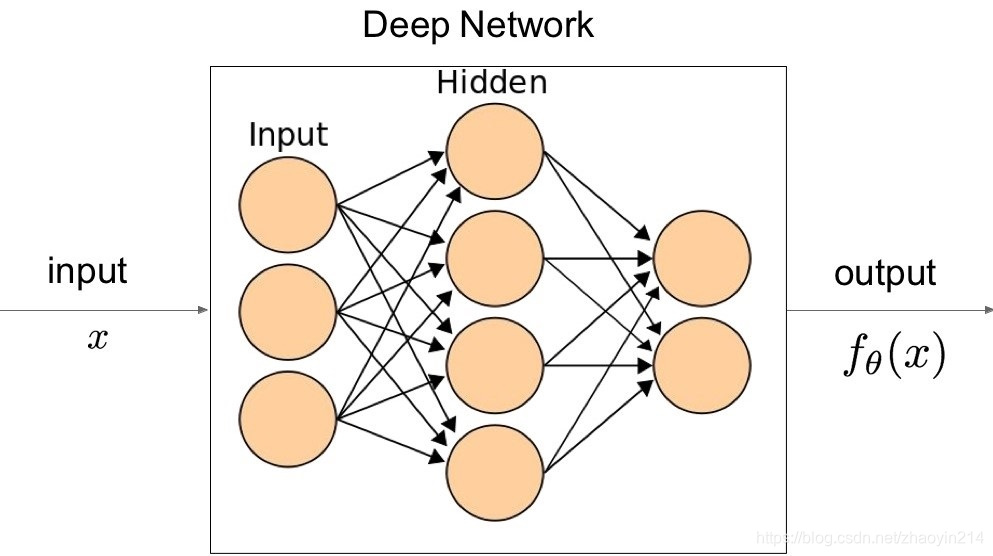
• 损失函数：衡量网络输出和真实值的差异

$$L(\theta )=\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{c}\mathrm{e}\left(f_{\theta }(x),y\right)$$

（1）损失函数并不使用测试数据（test & validation data）来衡量网络的性能；

（2）损失函数用来指导训练过程，使得网络的参数向损失降低的方向改变。

• 训练过程

随机梯度下降法（Stochastic gradient descent）

（1）试图找到一组参数使得损失函数的值越小越好；

（2）调整参数的大小和方向取决于损失函数相对于参数的偏导数：$\frac{\partial L}{\partial w}$，$\frac{\partial L}{\partial b}$

• 特性

（1）当网络的输出和真实输出一致时，损失函数值最小（0）；

（2）输出和真实输出越不一致，损失函数值越大。

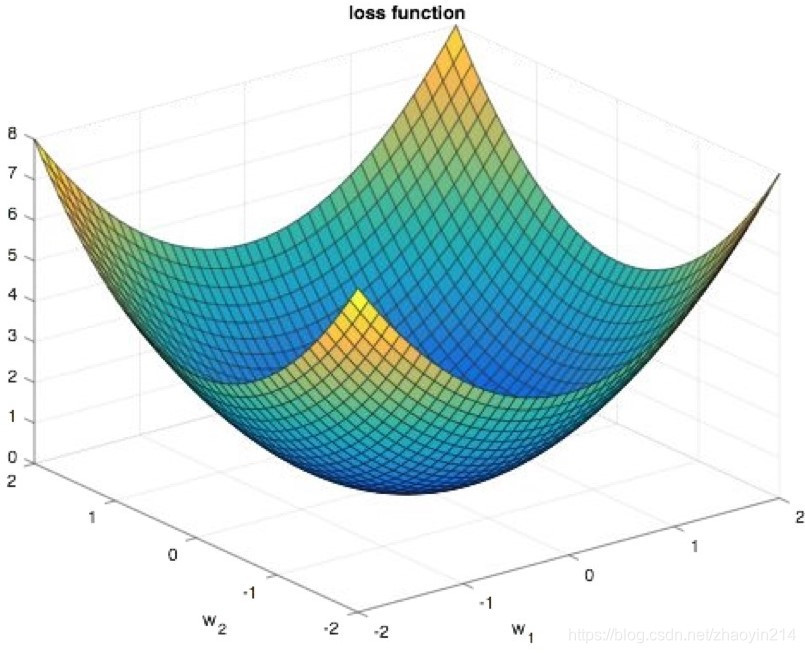
（3）理想情况：凸函数（convex）

（4）实际情况：非凸函数（not convex）

损失函数需要根据输出的变化而平滑的变化：（1）可导（SGD优化）；（2）容易求导

• 前提

为了使得误差向后传递（backpropagation）工作：

（1）损失函数为每一个独立训练样本损失的均值

$$L=\frac{1}{m}\sum _{i=1}^m{L}_i$$

$L$称为经验风险（empirical risk）

（2）损失函数为网络输出的函数

常用的损失函数

• 不同的任务类型需要不同的损失函数

（1）回归（Regression）：网络输出一个连续的数值

例如：预测一栋房屋的价值

损失函数：绝对值误差、平方差

（2）分类（Classification）：网络的输出为一个类别，从预定义的一组类别中选择一个

实例：判断邮件是否是垃圾邮件

损失函数：合页损失（hinge loss）、交叉熵（Cross-entropy loss）

回归

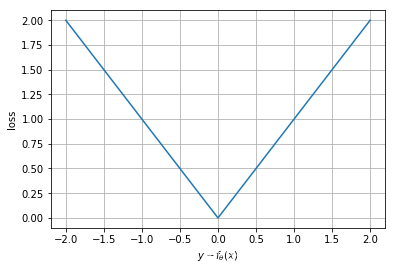
• 绝对误差函数（Absolute value，$l_1$-norm）：非常质感的损失函数

$$L=\frac{1}{m}\sum _{i=1}^m\left|y_i-f_{\theta }(x_i)\right|$$

（1）得到的解会比较稀疏sparser

在高维度任务中表现比较好

预测速度快

（2）对异常值（outliers）不敏感

%matplotlib inline

import matplotlib.pyplot as plt
import numpy as np

x = np.linspace(-2, 2, 51)
y = np.abs(x)

fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(x, y)
ax.grid(True)
ax.set_xlabel(r"$y - f_{\theta} (x)$")
ax.set_ylabel(r"loss")
plt.show()

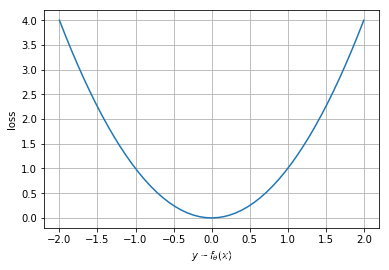
• 方差函数（Square error，Euclidean loss，$L_2$-norm）：常用的损失函数

$$L=\frac{1}{m}\sum _{i=1}^m{\left(y_i-f_{\theta }(x_i)\right)}^2$$

（1）比绝对误差函数输出结果更精准

（2）对大的误差输出更敏感

（3）对异常值（outliers）很敏感

x = np.linspace(-2, 2, 51)
y = x ** 2

fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(x, y)
ax.grid(True)
ax.set_xlabel(r"$y - f_{\theta} (x)$")
ax.set_ylabel(r"loss")
plt.show()

PS：敏感是指误差函数非线性特性，误差函数对大的误差（或异常值）敏感是指其对大的误差（或异常值）的输出相对于其对小的误差（或正常值）的输出大于线性，即：

$$L(\alpha \Delta x)>\alpha L(\Delta x),\alpha \in R^{+}$$

分类

将输入分为固定的几个类别

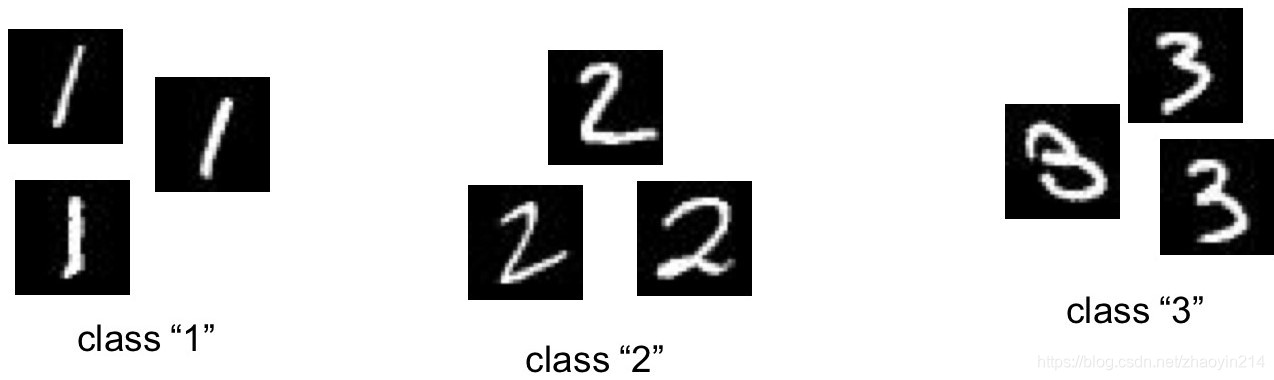
• 期望得到的结果是每一个输入对应一个类别输出

（1）网络的输出包含对每一个类别的预测值

（2）如果有$K$个类别，网络的输出为$K$维向量

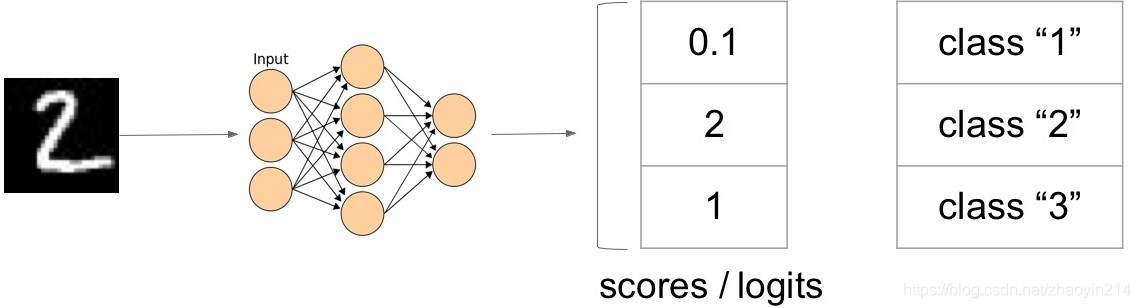
• 如何设计分类函数

（1）将样本的类别标签编码为一个向量$\to$独热编码（one-hot encoding）

（2）非概率解释$\to$合页函数（hinge loss）

（3）概率解释：将输出转换为概率函数$\to$Softmax

• Softmax

$$S(l_i)=\frac{e^{l_i}}{{\sum }_k{e}^{l_k}}$$

其中，$l_i$为scores（logits）

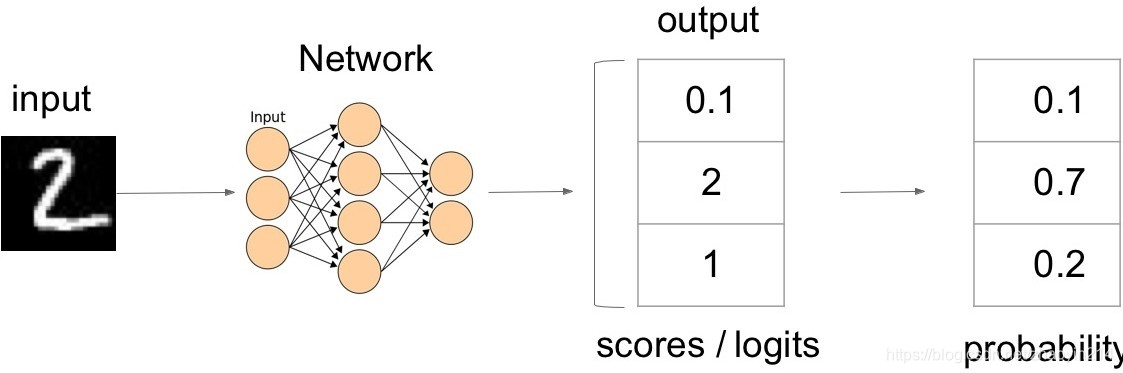
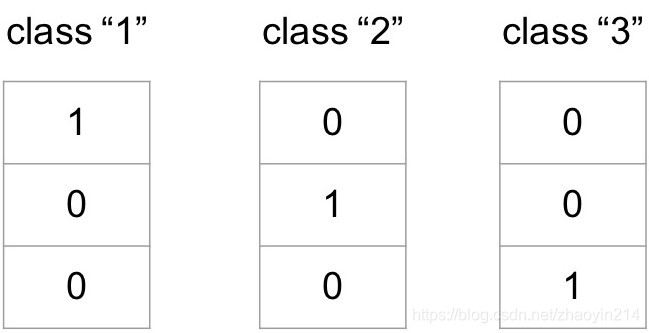
• 独热编码（One-hot encoding）

将每条样本的类别标签转换成对应的向量（每个向量元素的值为1或者0）

（1）向量维数为类别数量$K$；

（2）元素1的位置对应样本的类别标签在标签集合中的索引。

• 交叉熵（Cross-entropy loss）

样本标签采用独热编码方式，即编码后标签为一$K$维向量：

$$\mathbf{y}={\left[y_1,y_2,\cdots ,y_K\right]}^{\mathrm{T}}$$

第$i$条样本的独热编码标签记为${\mathbf{y}}_i$，Softmax输入向量记为${\mathbf{l}}_i=f_{\theta }({\mathbf{x}}_i)$，则第$i$条样本的交叉熵表示为：

$$\begin{array}{rl}{L}_i=& -\sum _{k=1}^K{y}_{i,k}\log \left(S_k({\mathbf{l}}_i)\right)\\ =& -{\mathbf{y}}_i^T\cdot \log \left[S({\mathbf{l}}_i)\right]\\ =& -{\mathbf{y}}_i^T\cdot \log \left[S\left(f_{\theta }({\mathbf{x}}_i)\right)\right]\end{array}$$

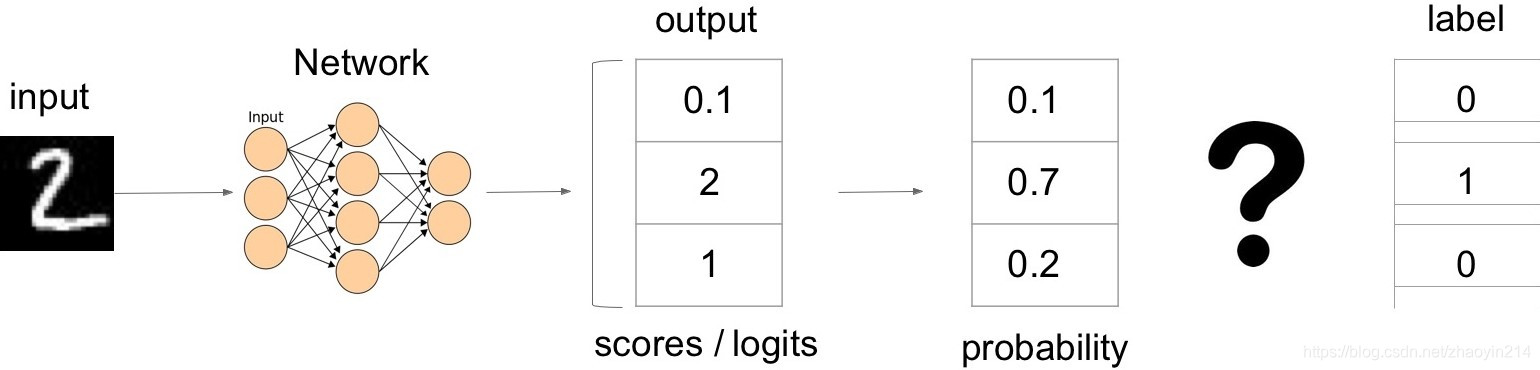
x = np.linspace(1e-5, 1, 1e3)
y = -1 * np.log(x)

fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(x, y)
ax.grid(True)
ax.set_xlabel(r"$x$")
ax.set_ylabel(r"- $\log$")
plt.show()

D:\ProgramData\Anaconda3\envs\greedyai\lib\site-packages\ipykernel_launcher.py:1: DeprecationWarning: object of type <class 'float'> cannot be safely interpreted as an integer.
  """Entry point for launching an IPython kernel.

对于包含$m$个样本的批输入，其交叉熵为

$$\begin{array}{rl}L=& \frac{1}{m}\sum _{i=1}^m{L}_i\\ =& -\frac{1}{m}\sum _{i=1}^m{\mathbf{y}}_i^T\cdot \log \left[S\left(f_{\theta }({\mathbf{x}}_i)\right)\right]\\ =& \frac{1}{m}\sum _{i=1}^m\sum _{k=1}^K{L}_{i,k}\\ =& -\frac{1}{m}\sum _{i=1}^m\sum _{k=1}^K{y}_{i,k}\log \left[S_k\left(f_{\theta }({\mathbf{x}}_i)\right)\right]\end{array}$$

一般而言，在分类问题中，交叉熵函数表现优于方差函数：

（1）方差函数对误差的输出惩罚非常大

（2）如果使用Softmax作为激活函数，方差函数作为损失函数，则梯度中包含${\hat{y}}_k(1-{\hat{y}}_k)$（${\hat{y}}_k$为Softmax输出列向量的第$k$个元素），当输出接近0.0或者1.0时，梯度值非常小，网络训练会很慢。

二分类任务中，方差损失与交叉熵损失

考虑二分类任务，分类器结构采用单层网络、激活函数为Sigmoid，网络输入为${\mathbf{x}}_i$、输出为${\hat{y}}_i$

$i$：样本索引

${\mathbf{x}}_i=\left[x_{i,1},x_{i,2},\cdots ,x_{i,n}\right]$：第$i$条样本，$n$维列向量

${\hat{y}}_i$：第$i$条样本估计，标量；

$y_i$：第$i$条样本的标签，标量；

$\theta$：单层网络权值系数向量，$n\times 1$维，${\left[{\theta }_j\right]}_{n\times 1}$

$b$：单层网络偏置系数，标量

• 方差函数的梯度（Gradient of square error loss）

预测：
$${\hat{y}}_i=\sigma ({\theta }^{\mathrm{T}}{\mathbf{x}}_i+b)$$

损失：
$$\begin{array}{rl}{L}_i=& \frac{1}{2}{\Vert y_i-{\hat{y}}_i\Vert }^2\\ =& \frac{1}{2}{\left(y_i-{\hat{y}}_i\right)}^2\end{array}$$

损失函数关于${\theta }_j$的梯度：

$$\frac{\partial L_i}{\partial {\theta }_j}=\frac{\partial L_i}{\partial {\hat{y}}_i}\frac{\partial {\hat{y}}_i}{\partial {\theta }_j}$$

（1）$L_i$关于${\hat{y}}_i$的偏导：

$$\frac{\partial L_i}{\partial {\hat{y}}_i}=\left({\hat{y}}_i-y_i\right)$$

（2）${\hat{y}}_i$关于${\theta }_j$的偏导：

$$\begin{array}{rl}{\hat{y}}_i=& \sigma \left({\theta }^{\mathrm{T}}{\mathbf{x}}_i+b\right)=\frac{1}{1+e^{-\left({\theta }^{\mathrm{T}}{\mathbf{x}}_i+b\right)}}\end{array}$$

$$\begin{array}{rl}\frac{\partial {\hat{y}}_i}{\partial {\theta }_j}=& {\sigma }_k\left(1-{\sigma }_k\right)x_{i,j}\\ =& {\hat{y}}_i\left(1-{\hat{y}}_i\right)x_{i,j}\end{array}$$

即

$$\frac{\partial L_i}{\partial {\theta }_j}=\left({\hat{y}}_i-y_i\right){\hat{y}}_i\left(1-{\hat{y}}_i\right)x_{i,j}$$

注意：${\hat{y}}_i\in (0,1)$，因此当${\hat{y}}_i\to 1\text{or}0$时，无论${\hat{y}}_i$是否趋近于$y_i$（即无论样本是否被正确分类，或损失函数是否到达关于样本$i$的极小值点），都有$\frac{\partial L_i}{\partial {\theta }_j}\to 0,\forall j$，即损失函数梯度消失，权值系数向量$\theta$更新近似停止。

• 交叉熵函数的梯度（Gradient of cross-entropy loss）

预测：
$${\hat{y}}_i=\sigma (\theta {\mathbf{x}}_i+b)$$

损失：
$$\begin{array}{rl}{L}_i=& \sum _{k=1}^2{L}_i\\ =& -y_i\log \left[{\hat{y}}_i\right]-(1-y_i)\log \left[1-{\hat{y}}_i\right]\\ =& -y_i\log \left[{\sigma }_k\left(\theta {\mathbf{x}}_i+b\right)\right]-(1-y_i)\log \left[1-{\sigma }_k\left(\theta {\mathbf{x}}_i+b\right)\right]\end{array}$$

损失函数关于${\theta }_j$的梯度：

$$\frac{\partial L_i}{\partial {\theta }_j}=\frac{\partial L_i}{\partial {\hat{y}}_i}\frac{\partial {\hat{y}}_i}{\partial {\theta }_j}$$

（1）$L_i$关于${\hat{y}}_i$的偏导：

$$\frac{\partial L_i}{\partial {\hat{y}}_i}=-\frac{y_i}{{\hat{y}}_i}+\frac{1-y_i}{1-{\hat{y}}_i}=-\frac{(y_i-{\hat{y}}_i)}{{\hat{y}}_i(1-{\hat{y}}_i)}$$

（2）${\hat{y}}_i$关于${\theta }_j$的偏导：

$$\begin{array}{rl}\frac{\partial {\hat{y}}_i}{\partial {\theta }_j}=& {\hat{y}}_i\left(1-{\hat{y}}_i\right)x_{i,j}\end{array}$$

即

$$\begin{array}{rl}\frac{\partial L_i}{\partial {\theta }_j}=& -(y_i-{\hat{y}}_i)x_{i,j}\end{array}$$

注意：${\hat{y}}_i\in (0,1)$，仅当${\hat{y}}_i\to y_i$时，即样本被正确分类（损失函数关于样本$i$的极小值点），损失函数关于${\theta }_j$的梯度才会消失，权值系数向量$\theta$更新停止。

多分类任务中，方差损失与交叉熵损失

考虑多分类任务，分类器结构采用单层网络、激活函数为Softmax，网络输入为${\mathbf{x}}_i$、输出为${\hat{\mathbf{y}}}_i$

$i$：样本索引

${\mathbf{x}}_i=\left[x_{i,1},x_{i,2},\cdots ,x_{i,n}\right]$：第$i$条样本，$n$维列向量

${\hat{\mathbf{y}}}_i=\left[{\hat{y}}_{i,1},{\hat{y}}_{i,2},\cdots ,{\hat{y}}_{i,k},\cdots ,{\hat{y}}_{i,K}\right]$：第$i$条样本估计，$K$维列向量；

${\mathbf{y}}_i$：第$i$条样本独热编码标签，$K$维列向量

$\theta$：单层网络权值系数矩阵，$K\times n$维，${\left[{\theta }_{kj}\right]}_{K\times n}$

$\mathbf{b}=\left[b_1,b_2,\cdots ,b_K\right]$：单层网络偏置系数，$K$维列向量

• 方差函数的梯度（Gradient of square error loss）

预测：
$${\hat{\mathbf{y}}}_i=S(\theta {\mathbf{x}}_i+\mathbf{b})$$

损失：
$$\begin{array}{rl}{L}_i=& \frac{1}{2}{\Vert {\mathbf{y}}_i-{\hat{\mathbf{y}}}_i\Vert }^2\\ =& \frac{1}{2}{\left({\mathbf{y}}_i-{\hat{\mathbf{y}}}_i\right)}^T\left({\mathbf{y}}_i-{\hat{\mathbf{y}}}_i\right)\\ =& \sum _k{L}_{i,k}\\ =& \frac{1}{2}\sum _k{\left(y_{i,k}-{\hat{y}}_{i,k}\right)}^2\end{array}$$

损失函数关于${\theta }_{k,j}$的梯度：

$$\frac{\partial L_i}{\partial {\theta }_{k,j}}=\frac{\partial L_i}{\partial {\hat{y}}_{i,k}}\frac{\partial {\hat{y}}_{i,k}}{\partial {\theta }_{k,j}}+\sum _{l̸=k}\frac{\partial L_i}{\partial {\hat{y}}_{i,l}}\frac{\partial {\hat{y}}_{i,l}}{\partial {\theta }_{l,j}}$$

（1）$L_i$关于${\hat{y}}_{i,k}$的偏导：

$$\frac{\partial L_i}{\partial {\hat{y}}_{i,k}}=\left({\hat{y}}_{i,k}-y_{i,k}\right)$$

（2）${\hat{y}}_{i,k}$关于${\theta }_{k,j}$的偏导：

$$\begin{array}{rl}{\hat{\mathbf{y}}}_i=& S\left(\theta {\mathbf{x}}_i+\mathbf{b}\right)=\frac{e^{\theta {\mathbf{x}}_i+\mathbf{b}}}{\sum e^{\theta {\mathbf{x}}_i+\mathbf{b}}}\\ {\hat{y}}_{i,k}=& S_k\left(\theta {\mathbf{x}}_i+\mathbf{b}\right)=\frac{e^{{\theta }_{[k,:]}{\mathbf{x}}_i+b_k}}{{\sum }_k{e}^{{\theta }_{[k,:]}{\mathbf{x}}_i+b_k}}\end{array}$$

$$\begin{array}{rl}\frac{\partial {\hat{y}}_{i,k}}{\partial {\theta }_{k,j}}=& S_k\left(1-S_k\right)x_{i,j}\\ =& {\hat{y}}_{i,k}\left(1-{\hat{y}}_{i,k}\right)x_{i,j}\end{array}$$

（3）${\hat{y}}_{i,l}$（$l̸=k$）关于${\theta }_{k,j}$的偏导：

$${\hat{y}}_{i,l}=S_l\left(\theta {\mathbf{x}}_i+\mathbf{b}\right)=\frac{e^{{\theta }_{[l,:]}{\mathbf{x}}_i+b_l}}{{\sum }_k{e}^{{\theta }_{[k,:]}{\mathbf{x}}_i+b_k}}$$

$$\begin{array}{rl}\frac{\partial {\hat{y}}_{i,l}}{\partial {\theta }_{k,j}}=& -S_k{S}_l{x}_{i,j}\\ =& -{\hat{y}}_{i,k}{\hat{y}}_{i,l}{x}_{i,j}\end{array}$$

即

$$\frac{\partial L_i}{\partial {\theta }_{k,j}}=\left({\hat{y}}_{i,k}-y_{i,k}\right){\hat{y}}_{i,k}\left(1-{\hat{y}}_{i,k}\right)x_{i,j}-\sum _{l̸=k}\left({\hat{y}}_{i,l}-y_{i,l}\right){\hat{y}}_{i,k}{\hat{y}}_{i,l}{x}_{i,j}$$

注意：${\hat{y}}_{i,k}\in [0,1]$且${\sum }_k{\hat{y}}_{i,k}=1$，因此当${\hat{y}}_{i,r}\to 1,\forall r$时，${\hat{y}}_{i,l|l̸=r}\to 0$或者$\left(1-{\hat{y}}_{i,k|k=r}\right)\to 0$，此时$\frac{\partial L_i}{\partial {\theta }_{k,j}}\to 0,\forall k,j$，即无论${\hat{\mathbf{y}}}_i$是否趋近于${\mathbf{y}}_i$（无论样本是否被正确分类，或者损失函数是否到达关于样本$i$的极小值点），损失函数梯度都会消失，权值系数矩阵$\theta ={\left[{\theta }_{kj}\right]}_{K\times n}$更新近似停止。

• 交叉熵函数的梯度（Gradient of cross-entropy loss）

预测：
$${\hat{\mathbf{y}}}_i=S(\theta {\mathbf{x}}_i+\mathbf{b})$$

损失：
$$\begin{array}{rl}{L}_i=& \sum _{k=1}^K{L}_{i,k}\\ =& -\sum _{k=1}^K{y}_{i,k}\log {\hat{y}}_{i,k}\\ =& -\sum _{k=1}^K{y}_{i,k}\log \left[S_k\left(\theta {\mathbf{x}}_i+\mathbf{b}\right)\right]\end{array}$$

损失函数关于${\theta }_{k,j}$的梯度：

$$\frac{\partial L_i}{\partial {\theta }_{k,j}}=\frac{\partial L_i}{\partial {\hat{y}}_{i,k}}\frac{\partial {\hat{y}}_{i,k}}{\partial {\theta }_{k,j}}+\sum _{l̸=k}\frac{\partial L_i}{\partial {\hat{y}}_{i,l}}\frac{\partial {\hat{y}}_{i,l}}{\partial {\theta }_{l,j}}$$

（1）$L_i$关于${\hat{y}}_{i,k}$的偏导：

$$\frac{\partial L_i}{\partial {\hat{y}}_{i,k}}=-\frac{y_{i,k}}{{\hat{y}}_{i,k}}$$

（2）${\hat{y}}_{i,k}$关于${\theta }_{k,j}$的偏导：

$$\begin{array}{rl}\frac{\partial {\hat{y}}_{i,k}}{\partial {\theta }_{k,j}}=& {\hat{y}}_{i,k}\left(1-{\hat{y}}_{i,k}\right)x_{i,j}\end{array}$$

（3）${\hat{y}}_{i,l}$（$l̸=k$）关于${\theta }_{k,j}$的偏导：

$$\begin{array}{rl}\frac{\partial {\hat{y}}_{i,l}}{\partial {\theta }_{k,j}}=& -{\hat{y}}_{i,k}{\hat{y}}_{i,l}{x}_{i,j}\end{array}$$

即

$$\begin{array}{rl}\frac{\partial L_i}{\partial {\theta }_{k,j}}=& -\frac{y_{i,k}}{{\hat{y}}_{i,k}}{\hat{y}}_{i,k}\left(1-{\hat{y}}_{i,k}\right)x_{i,j}+\sum _{l̸=k}\frac{y_{i,l}}{{\hat{y}}_{i,l}}{\hat{y}}_{i,k}{\hat{y}}_{i,l}{x}_{i,j}\\ =& -y_{i,k}\left(1-{\hat{y}}_{i,k}\right)x_{i,j}+\sum _{l̸=k}{y}_{i,l}{\hat{y}}_{i,k}{x}_{i,j}\end{array}$$

注意：${\hat{y}}_{i,k}\in [0,1]$且${\sum }_k{\hat{y}}_{i,k}=1$，因此当${\hat{y}}_{i,r}\to 1,\forall r$时，${\hat{y}}_{i,l|l̸=r}\to 0$或者$\left(1-{\hat{y}}_{i,k|k=r}\right)\to 0$，此时$\frac{\partial L_i}{\partial {\theta }_{k,j}}\approx {\sum }_{l̸=k}{y}_{i,l}{x}_{i,j},k=r,\forall j$或者$\frac{\partial L_i}{\partial {\theta }_{k,j}}\approx -y_{i,k}{x}_{i,j},\forall j,k̸=r$。仅当${\hat{\mathbf{y}}}_i\to {\mathbf{y}}_i$时，即样本被正确分类（损失函数关于样本$i$的极小值点），损失函数关于${\theta }_{k,j}$的梯度才会消失，权值系数矩阵$\theta ={\left[{\theta }_{kj}\right]}_{K\times n}$更新停止。

PS：上述推导过程是针对单样本的损失函数$L_i$进行的，对于批量梯度下降，损失函数$L=\frac{1}{m}{\sum }_{i=1}^m{L}_i$，此时，

（1）对于方差损失，只要大多数样本预测向量中包含${\hat{y}}_{i,k}\to 1$（无论这些样本是否被正确分类），损失函数梯度就会消失，权值系数$\theta$更新近似停止，即训练过程可能陷入鞍点（saddle point），而难以到达方差损失的局部极小值点。

（2）对于交叉熵损失，只有当大多数样本预测向量否被正确分类时，损失函数梯度才会消失，权值系数$\theta$更新停止，交叉熵损失到达局部极小值而不会陷入鞍点。

• 多标签（Multi-label）分类问题

多标签分类问题不是多分类（Multi-class）问题

（1）输出属于多个类别中的一个或者多个类；

例如：一幅包含猫咪的图像可以同时属于“猫”、“哺乳动物”和“宠物”类别。

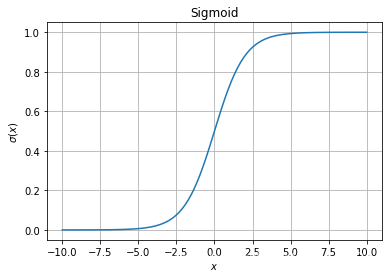
（2）对每一个输出独立使用Sigmoid（$\sigma (\cdot )$）作为激活函数，而非Softmax；

$$\sigma \left(l_i\right)=\frac{1}{1+e^{-l_i}}$$

def sigmoid(x):
    return 1 / (1 + np.exp(-1 * x))

x = np.linspace(-10, 10, 100)
y = sigmoid(x)

fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(x, y)
ax.grid(True)
ax.set_xlabel("$x$")
ax.set_ylabel("$\\sigma(x)$")
ax.set_title("Sigmoid")
plt.show()

（3）多标签问题的交叉熵损失（Cross-entropy loss for multi-label classification）

$$\begin{array}{rl}{L}_i=& -\sum _{k=1}^K{y}_{i,k}\log \left[\sigma \left(f_{\theta ,k}({\mathbf{x}}_i)\right)\right]+(1-y_{i,k})\log \left[1-\sigma \left(f_{\theta ,k}({\mathbf{x}}_i)\right)\right]\end{array}$$

（4）多分类问题的交叉熵损失（Cross-entropy loss for multi-class classification）

$$\begin{array}{rl}{L}_i=& -\sum _{k=1}^K{y}_{i,k}\log \left[S_k\left(f_{\theta }({\mathbf{x}}_i)\right)\right]\end{array}$$

其中，$f_{\theta }\left({\mathbf{x}}_i\right)$是一个$K$维列向量，表示输出层激活函数的输入，$f_{\theta ,k}\left({\mathbf{x}}_i\right)$表示$f_{\theta }\left({\mathbf{x}}_i\right)$的第$k$个元素。

正则化

正则化（Regularization）：避免网络过拟合（prevent overfitting）

（1）$L_2$正则（$L_2$-regularization）权值衰减（weight decay）:

$$L_{\mathrm{r}\mathrm{e}\mathrm{g}}=L+\frac{\lambda }{2}{\Vert \theta \Vert }_2^2$$

（2）$L_1$-regularization：

$$L_{\mathrm{r}\mathrm{e}\mathrm{g}}=L+\frac{\lambda }{2}{\Vert \theta \Vert }_1$$

实例

平均交叉熵损失：

$$\begin{array}{rl}L=& \frac{1}{m}\sum _{i=1}^m{L}_i=-\frac{1}{m}\sum _{i=1}^m{\mathbf{y}}_i^T\cdot \log \left[S\left(f_{\theta }({\mathbf{x}}_i)\right)\right]\end{array}$$

平均方差损失：

$$\begin{array}{rl}L=& \frac{1}{m}\sum _{i=1}^m{L}_i=\frac{1}{m}\sum _{i=1}^m\frac{1}{2}{\Vert {\mathbf{y}}_i-{\hat{\mathbf{y}}}_i\Vert }^2\end{array}$$

例1：

网络输出（Softmax）	真实输出	是否正确
0.3, 0.3, 0.4	0 0 1	是
0.3, 0.4, 0.3	0 1 0	是
0.1, 0.2, 0.7	1 0 0	否

y_hat = np.array(
    [[0.3, 0.3, 0.4],
     [0.3, 0.4, 0.3],
     [0.1, 0.2, 0.7]])

y = np.array(
    [[0, 0, 1],
     [0, 1, 0],
     [1, 0, 0]])

avg_classification_acc = np.array([np.argmax(y[idx]) == np.argmax(y_hat[idx]) for idx in range(3)]).sum() / 3
avg_cross_entropy_loss = -1 * np.array([np.dot(y[idx], np.log(y_hat[idx])) for idx in range(3)]).sum() / 3
avg_square_error_loss = np.array([np.dot(y[idx] - y_hat[idx], y[idx] - y_hat[idx]) for idx in range(3)]).sum() / 3
print("average classification accuracy: {}".format(avg_classification_acc))
print("average cross entropy loss: {}".format(avg_cross_entropy_loss))
print("average square error loss: {}".format(avg_square_error_loss))

average classification accuracy: 0.6666666666666666
average cross entropy loss: 1.3783888522474517
average square error loss: 0.8066666666666666

例2：

网络输出（Softmax）	真实输出	是否正确
0.1, 0.2, 0.7	0 0 1	是
0.1, 0.7, 0.2	0 1 0	是
0.3, 0.4, 0.3	1 0 0	否

y_hat = np.array(
    [[0.1, 0.2, 0.7],
     [0.1, 0.7, 0.2],
     [0.3, 0.4, 0.3]])

y = np.array(
    [[0, 0, 1],
     [0, 1, 0],
     [1, 0, 0]])

avg_classification_acc = np.array([np.argmax(y[idx]) == np.argmax(y_hat[idx]) for idx in range(3)]).sum() / 3
avg_cross_entropy_loss = -1 * np.array([np.dot(y[idx], np.log(y_hat[idx])) for idx in range(3)]).sum() / 3
avg_square_error_loss = np.array([np.dot(y[idx] - y_hat[idx], y[idx] - y_hat[idx]) for idx in range(3)]).sum() / 3
print("average classification accuracy: {}".format(avg_classification_acc))
print("average cross entropy loss: {}".format(avg_cross_entropy_loss))
print("average square error loss: {}".format(avg_square_error_loss))

average classification accuracy: 0.6666666666666666
average cross entropy loss: 0.6391075640678003
average square error loss: 0.34