学习笔记 - GreedyAI - DeepLearningCV - Lesson2 Neural-Network

第5章 神经网络

任务学习27: 神经网络分类问题的经典数据（集鸢尾花数据集）介绍，神经网络Python库Keras的介绍

import numpy as np
import pandas as pd
from keras.models import Sequential
from keras.layers import Dense
from keras.wrappers.scikit_learn import KerasClassifier
from keras.utils import np_utils
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import KFold
from sklearn.preprocessing import LabelEncoder
from keras.models import model_from_json

Using TensorFlow backend.

# reproducibility
seed = 13
np.random.seed(seed)

任务学习28: 使用Pandas读取鸢尾花数据集， 使用LabelEncoder对类别标签进行编码

# load data
df = pd.read_csv("./data/iris.csv") # header自动推理，首行为特征名称

# 样本类型：float
X = df.values[:, 0 : 4].astype(np.float)

# 标签：独热编码
Y = df.values[:, 4]
encoder = LabelEncoder()
Y_encoded = encoder.fit_transform(Y)
Y_onehot = np_utils.to_categorical(Y_encoded)

任务学习29: 使用Keras创建一个用于鸢尾花分类识别的神经网络

Keras的目标是搭建模型，最主要的模型是Sequential：不同层的叠加。模型创建后可以编译，调用后端进行优化，可以指定损失函数和优化算法。

• 定义模型：创建Sequential模型，加入每一层
• 编译模型：指定损失函数和优化算法，使用模型的compile()方法
• 拟合数据：使用模型的fit()方法拟合数据
• 进行预测：使用模型的evaluate() 或 predict()方法进行预测

# define a network
def baseline_model():
    model = Sequential()
    model.add(Dense(7, input_dim=4, activation="tanh"))
    model.add(Dense(3, activation="softmax"))
    model.compile(loss="mean_squared_error", optimizer="sgd", metrics=["accuracy"])
    return model

estimator = KerasClassifier(build_fn=baseline_model, epochs=20, batch_size=1, verbose=1)

# evalute
kfold = KFold(n_splits=10, shuffle=True, random_state=seed)
result = cross_val_score(estimator, X, Y_onehot, cv=kfold)
print("Accuracy of cross validation, mean {:.2f}, std {:.2f}".format(result.mean(), result.std()))

# save model
estimator.fit(X, Y_onehot)
model_json = estimator.model.to_json()
with open("model.json", "w") as json_file:
    json_file.write(model_json)
    
estimator.model.save_weights("model.h5")
print("saved model to disk")

# load model and use it for prediction
with open("model.json", "r") as json_file:
    loaded_model_json = json_file.read()
    
loaded_model = model_from_json(loaded_model_json)
loaded_model.load_weights("model.h5")
print("loaded model from disk")

predicted = loaded_model.predict(X)
print("predicted probability: {}".format(predicted))

predicted_label = loaded_model.predict_classes(X)
print("predicted label: {}".format(predicted_label))

Epoch 1/20
135/135 [==============================] - 4s 28ms/step - loss: 0.2443 - acc: 0.3407
Epoch 2/20
135/135 [==============================] - 0s 3ms/step - loss: 0.2072 - acc: 0.5704
...
Epoch 15/20
135/135 [==============================] - 0s 3ms/step - loss: 0.1035 - acc: 0.8222
Epoch 16/20
135/135 [==============================] - 0s 3ms/step - loss: 0.1018 - acc: 0.8519
Epoch 17/20
135/135 [==============================] - 0s 3ms/step - loss: 0.0990 - acc: 0.8296
Epoch 18/20
135/135 [==============================] - 0s 3ms/step - loss: 0.0956 - acc: 0.8815
Epoch 19/20
135/135 [==============================] - 0s 3ms/step - loss: 0.0911 - acc: 0.8889
Epoch 20/20
135/135 [==============================] - 0s 3ms/step - loss: 0.0897 - acc: 0.9185
15/15 [==============================] - 0s 6ms/step
Accuracy of cross validation, mean 0.88, std 0.10
Epoch 1/20
150/150 [==============================] - 1s 4ms/step - loss: 0.2743 - acc: 0.3000
Epoch 2/20
150/150 [==============================] - 0s 3ms/step - loss: 0.2330 - acc: 0.5667
...
Epoch 20/20
150/150 [==============================] - 0s 2ms/step - loss: 0.0893 - acc: 0.9267
saved model to disk
loaded model from disk
predicted probability: [[0.8176712  0.15703547 0.02529336]
 [0.78485036 0.18383005 0.0313196 ]
 [0.80815816 0.16466351 0.02717836]
 [0.7999122  0.1710709  0.02901697]
 [0.8235647  0.15209858 0.02433665]
 [0.8198723  0.15501045 0.02511729]
 [0.81340504 0.15997025 0.02662468]
 [0.81267214 0.16101956 0.02630831]
 [0.789584   0.1793422  0.03107387]
 [0.8007948  0.17074902 0.02845627]
 [0.822006   0.15354557 0.02444837]
 [0.81417686 0.15948814 0.02633505]
 [0.79659516 0.1741767  0.0292281 ]
 [0.8113598  0.16196024 0.02667985]
 [0.83054143 0.14667283 0.02278574]
 [0.8353478  0.14245501 0.02219726]
 [0.82393813 0.15193452 0.02412729]
 [0.8122542  0.16144124 0.0263046 ]
 [0.8156125  0.15883708 0.02555045]
 [0.82518315 0.15065108 0.02416579]
 [0.8016695  0.17022601 0.0281045 ]
 [0.81624687 0.1579284  0.0258247 ]
 [0.8303179  0.14657274 0.02310932]
 [0.7731797  0.19280624 0.03401403]
 [0.80916727 0.16317779 0.02765493]
 [0.77769333 0.18957365 0.03273295]
 [0.79727    0.17332435 0.02940557]
 [0.8149991  0.15923807 0.02576284]
 [0.80999875 0.1634253  0.02657591]
 [0.8035455  0.1680961  0.02835841]
 [0.79377735 0.17622194 0.03000078]
 [0.788363   0.18118247 0.03045458]
 [0.8381295  0.14012037 0.02175012]
 [0.8372635  0.1409427  0.02179371]
 [0.8007948  0.17074902 0.02845627]
 [0.80274093 0.16941263 0.02784647]
 [0.8108503  0.16289848 0.02625112]
 [0.8007948  0.17074902 0.02845627]
 [0.799757   0.17120945 0.0290335 ]
 [0.81088346 0.16256839 0.02654814]
 [0.8150729  0.1591214  0.02580569]
 [0.6807096  0.26658523 0.05270518]
 [0.8125231  0.16075203 0.02672486]
 [0.7875169  0.18080136 0.03168177]
 [0.8146583  0.15867338 0.02666832]
 [0.7782834  0.18900636 0.03271019]
 [0.8280155  0.14832467 0.02365982]
 [0.8084066  0.16424385 0.02734955]
 [0.8233456  0.15238772 0.02426668]
 [0.80758554 0.1652878  0.02712665]
 [0.23777473 0.5072652  0.2549601 ]
 [0.16764162 0.47040772 0.36195064]
 [0.16765393 0.49012756 0.34221855]
 [0.14366542 0.4711359  0.38519865]
 [0.15185325 0.4839112  0.36423555]
 [0.12385198 0.43105912 0.4450889 ]
 [0.11556677 0.42305827 0.46137497]
 [0.27378893 0.47327596 0.25293517]
 [0.21536046 0.5046911  0.27994844]
 [0.12100814 0.42123288 0.45775893]
 [0.21526203 0.49691823 0.28781974]
 [0.14304878 0.45013008 0.4068211 ]
 [0.27006775 0.5166927  0.21323957]
 [0.12146756 0.44001967 0.43851274]
 [0.2538253  0.4775232  0.26865146]
 [0.24028768 0.5048216  0.25489074]
 [0.09102836 0.3839209  0.52505076]
 [0.2737403  0.48618653 0.24007323]
 [0.12572394 0.47346845 0.40080756]
 [0.23138559 0.49392    0.2746944 ]
 [0.06046253 0.34105137 0.5984861 ]
 [0.23798294 0.500442   0.261575  ]
 [0.09704993 0.43381125 0.46913886]
 [0.16243456 0.4705574  0.36700812]
 [0.23515466 0.5031155  0.26172987]
 [0.22256629 0.5045949  0.27283877]
 [0.1848549  0.5055306  0.30961454]
 [0.09643033 0.42837268 0.47519696]
 [0.11434723 0.43329504 0.4523577 ]
 [0.3438071  0.47962397 0.17656896]
 [0.22748403 0.49610215 0.27641386]
 [0.2732847  0.49544626 0.23126903]
 [0.24053998 0.4933921  0.26606795]
 [0.05850685 0.3545622  0.58693093]
 [0.08241262 0.36368605 0.5539014 ]
 [0.11929239 0.4065819  0.47412562]
 [0.17044769 0.48686126 0.342691  ]
 [0.18943594 0.51211977 0.29844427]
 [0.1807541  0.4495976  0.3696483 ]
 [0.15023798 0.4657722  0.38398975]
 [0.12887649 0.4378912  0.4332324 ]
 [0.13695171 0.44787776 0.4151705 ]
 [0.21752372 0.4955243  0.286952  ]
 [0.27231866 0.4847829  0.24289834]
 [0.14470318 0.4523037  0.4029931 ]
 [0.20874657 0.45905542 0.33219808]
 [0.16786517 0.45620543 0.37592936]
 [0.21103503 0.4923615  0.29660347]
 [0.32313448 0.47468314 0.20218243]
 [0.17509918 0.46781343 0.35708743]
 [0.02918322 0.27005574 0.700761  ]
 [0.039795   0.30593666 0.65426826]
 [0.04173652 0.3203026  0.63796085]
 [0.04284395 0.31537157 0.6417844 ]
 [0.03300598 0.28702676 0.6799673 ]
 [0.0381605  0.3104905  0.651349  ]
 [0.04405444 0.3066925  0.6492531 ]
 [0.04917131 0.34294397 0.60788476]
 [0.04615707 0.33496377 0.61887914]
 [0.03245904 0.28445876 0.6830822 ]
 [0.05310059 0.34205383 0.6048456 ]
 [0.04713838 0.33423537 0.61862624]
 [0.04401288 0.32553402 0.63045305]
 [0.03653352 0.29884395 0.66462255]
 [0.03082264 0.2782038  0.6909736 ]
 [0.036024   0.29495692 0.66901904]
 [0.05023248 0.33651078 0.61325675]
 [0.03700978 0.2984411  0.6645492 ]
 [0.03215639 0.29021433 0.6776293 ]
 [0.06888437 0.38797092 0.54314476]
 [0.03645117 0.3004284  0.66312045]
 [0.0383532  0.29806185 0.66358495]
 [0.04151791 0.3229704  0.63551176]
 [0.06468362 0.3763071  0.5590093 ]
 [0.03955726 0.30520573 0.65523696]
 [0.05655772 0.3567383  0.586704  ]
 [0.06532113 0.37389705 0.56078184]
 [0.05884918 0.3512941  0.5898568 ]
 [0.03544806 0.2969393  0.66761255]
 [0.08517325 0.41648743 0.49833935]
 [0.05427446 0.3591159  0.5866096 ]
 [0.05655151 0.35403892 0.5894096 ]
 [0.03356074 0.2907361  0.67570317]
 [0.08388655 0.40416887 0.5119446 ]
 [0.05560397 0.34830487 0.59609115]
 [0.04409329 0.33125734 0.62464935]
 [0.03239392 0.27883363 0.68877244]
 [0.04865128 0.32790133 0.62344736]
 [0.05949718 0.35074157 0.58976126]
 [0.0495043  0.34089735 0.60959834]
 [0.03333379 0.28977478 0.67689145]
 [0.04859672 0.34025255 0.6111507 ]
 [0.039795   0.30593666 0.65426826]
 [0.03327894 0.2883111  0.67840993]
 [0.03156257 0.28157383 0.6868636 ]
 [0.04115696 0.31749475 0.64134836]
 [0.05328796 0.35334325 0.5933688 ]
 [0.04875791 0.33554175 0.61570036]
 [0.03512155 0.28537518 0.67950326]
 [0.04782918 0.3202361  0.6319347 ]]
predicted label: [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 2 2 1 1 2 1 1 1 1 1 1 2 1 1 1 2 1 2 1
 1 1 1 2 2 1 1 1 1 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
 2 2]

任务学习30: 训练用于鸢尾花分类的神经网络 解读训练输出的日志 了解如何评价神经网络的性能

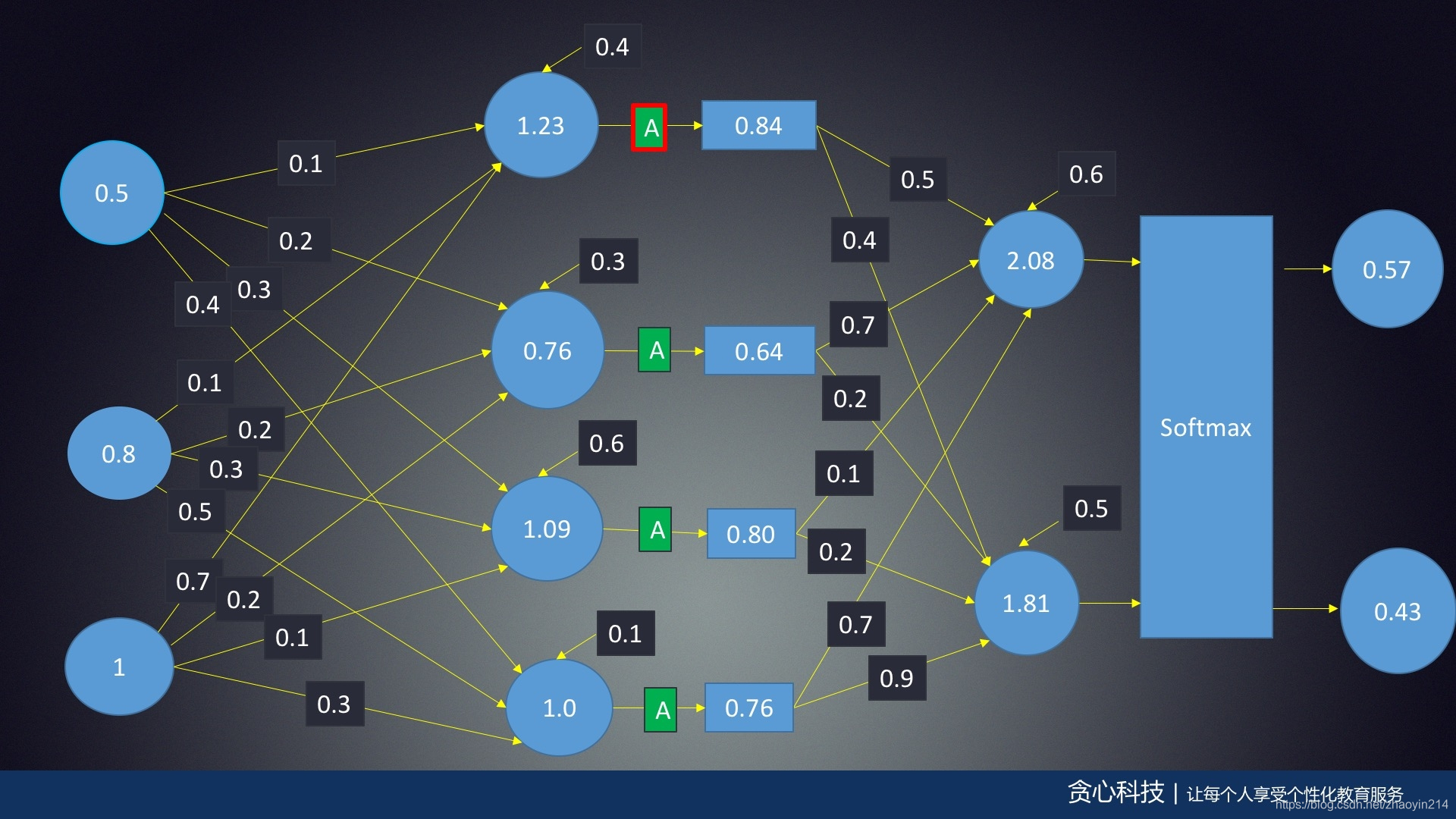
任务学习31: 神经网络数学原理（1）： 神经网络的结点，权值，激活函数

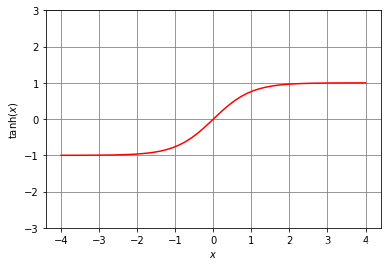
• 双曲正切激活函数（activation function）

$$\tanh (x)=\frac{\sinh (x)}{\cosh (x)}=\frac{e^x-e^{-x}}{e^x+e^{-x}}=\frac{e^{2x}-1}{e^{2x}+1}=\frac{1-e^{-2x}}{1+e^{-2x}}$$

$$\begin{array}{rl}\frac{\partial \tanh (x)}{\partial x}=& \frac{\partial \frac{e^x-e^{-x}}{e^x+e^{-x}}}{\partial x}=\frac{{\left(e^x+e^{-x}\right)}^2-{\left(e^x-e^{-x}\right)}^2}{{\left(e^x+e^{-x}\right)}^2}\\ =& 1-{\tanh }^2(x)=\left(1-\tanh (x)\right)\left(1+\tanh (x)\right)\end{array}$$

%matplotlib inline
import matplotlib.pyplot as plt

x = np.linspace(-4, 4)
y = np.tanh(x)

fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(x, y, color="red")
ax.set_xlabel("$x$")
ax.set_ylabel("$\mathrm{tanh}(x)$")
ax.set_ylim([-3, 3])
ax.grid(True, color="gray")

任务学习32: 神经网络数学原理（2）： 神经网络的前馈（Feed Forward）算法

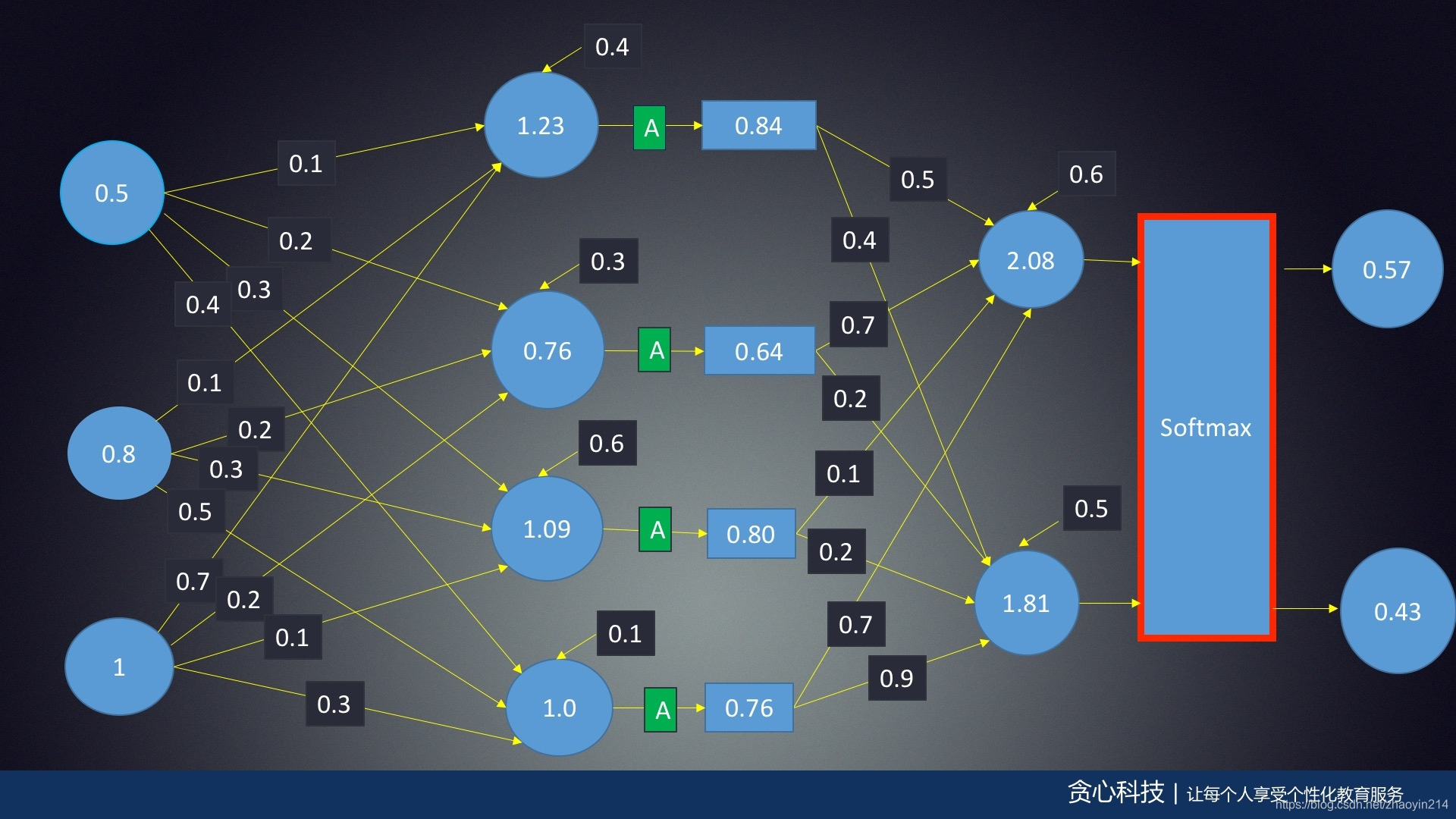
• Softmax（归一化指数函数，normalized exponential function）

$$\sigma :R^K\to \left\{z\in R^K\mid z_i>0,\sum _{i=1}^K{z}_i=1\right\}$$

$$\sigma (\mathbf{x}{)}_j=\frac{e^{x_j}}{{\sum }_{k=1}^K{e}^{x_k}},\text{for}j=1,2,\cdots ,K$$

$$\frac{\partial \sigma (\mathbf{x}{)}_j}{\partial x_j}=\frac{\partial \frac{e^{x_j}}{\sum e^{x_k}}}{\partial x_j}=\frac{e^{x_j}}{\sum e^{x_j}}-{\left(\frac{e^{x_j}}{\sum e^{x_j}}\right)}^2=\sigma (\mathbf{x}{)}_j\left(1-\sigma (\mathbf{x}{)}_j\right)$$

def softmax(x):
    x = np.array(x)
    return np.exp(x) / np.sum(np.exp(x))

print(softmax([1, 2, 3]))
print(softmax([1000, 2000, 3000]))

[0.09003057 0.24472847 0.66524096]
[nan nan nan]


D:\ProgramData\Anaconda3\envs\greedyai\lib\site-packages\ipykernel_launcher.py:3: RuntimeWarning: invalid value encountered in true_divide
  This is separate from the ipykernel package so we can avoid doing imports until

任务学习33: 神经网络数学原理（3）：神经网络的前馈（Feed Forward）算法续，Softmax层的数值问题

• Softmax数值问题 - 上溢（overflow）

$$\begin{array}{r}\sigma (\mathbf{x})=\frac{e^{\mathbf{x}}}{\sum e^{\mathbf{x}}}=\frac{e^{\mathbf{x}-m}}{\sum e^{\mathbf{x}-m}}\end{array}$$

def softmax(x):
    x = np.array(x)
    m = x.max()
    return np.exp(x - m) / np.sum(np.exp(x - m))

print(softmax([1, 2, 3]))
print(softmax([1000, 2000, 3000]))

[0.09003057 0.24472847 0.66524096]
[0. 0. 1.]

任务学习34: 神经网络数学原理（4）：神经网络BP（误差反向传播）算法

任务学习35: 神经网络数学原理（5）：神经网络BP（误差反向传递）算法续

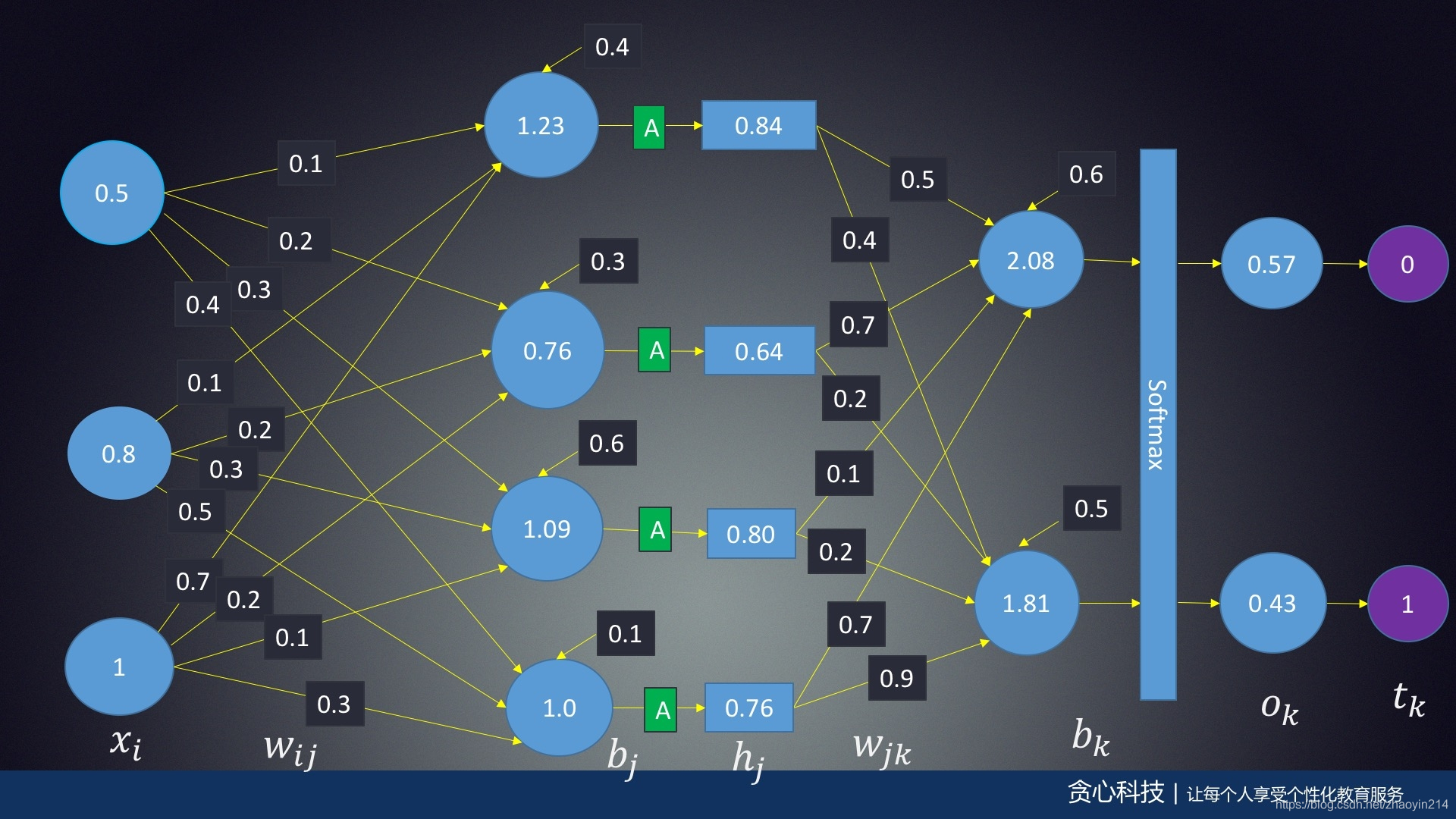
• 输入层：

$$\mathbf{x}=[x_1,x_2,\cdots ,x_n]$$

• 隐藏层$l_1$：

$${\mathbf{l}}_1=[l_{1,1},l_{1,2},\cdots ,l_{1,j},\cdots ],l_{1,j}={\mathbf{w}}_{1,j}^T\mathbf{x}+b_j$$

• 激活层$\tanh$

$$\mathbf{h}=[h_1,h_2,\cdots ,h_j,\cdots ],h_j=\tanh \left(l_{1,j}\right)=\frac{e^{2l_{1,j}}-1}{e^{2l_{1,j}}+1}$$

• 隐藏层$l_2$：

$${\mathbf{l}}_2=[l_{2,1},l_{2,2},\cdots ,l_{2,k},\cdots ],l_{2,k}={\mathbf{w}}_{2,k}^T\mathbf{h}+b_k$$

• 激活层$\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}$

$$\mathbf{o}=\sigma \left({\mathbf{l}}_2\right)=\frac{e^{{\mathbf{l}}_2}}{\sum e^{{\mathbf{l}}_2}},o_k=\frac{e^{l_{2,k}}}{\sum e^{l_{2,k}}}$$

• 样本标签

$$\mathbf{t}=[t_1,t_2,\cdots ,t_k,\cdots ]$$

• 损失函数

$$\begin{array}{rl}L=& \sum _k{L}_k\\ L_k=& \frac{1}{2}(t_k-o_k{)}^2=\frac{1}{2}{\left(t_k-\frac{e^{l_{2,k}}}{\sum e^{{\mathbf{l}}_2}}\right)}^2\end{array}$$

• $L_k$关于隐藏层$l_2$权重系数$w_{2,jk}$的导数

$$\begin{array}{rl}\frac{\partial l_{2,k}}{\partial w_{2,jk}}=& h_j\\ \frac{\partial o_k}{\partial l_{2,k}}=& \frac{\partial \frac{e^{l_{2,k}}}{\sum e^{l_{2,k}}}}{\partial l_{2,k}}=\frac{e^{l_{2,k}}}{\sum e^{l_{2,k}}}-{\left(\frac{e^{l_{2,k}}}{\sum e^{l_{2,k}}}\right)}^2=o_k\left(1-o_k\right)\\ \frac{\partial L_k}{\partial o_k}=& o_k-t_k\end{array}$$

因此

$$\begin{array}{rl}\frac{\partial L_k}{\partial w_{2,jk}}=& \frac{\partial L_k}{\partial o_k}\frac{\partial o_k}{\partial l_{2,k}}\frac{\partial l_{2,k}}{\partial w_{2,jk}}\\ =& h_j\left(o_k-t_k\right)o_k\left(1-o_k\right)\end{array}$$

• $L_k$关于隐藏层$l_2$偏置系数$b_{2,k}$的导数

$$\begin{array}{rl}\frac{\partial l_{2,k}}{\partial b_{2,k}}=& 1\end{array}$$

因此

$$\begin{array}{rl}\frac{\partial L_k}{\partial b_{2,k}}=& \frac{\partial L_k}{\partial o_k}\frac{\partial o_k}{\partial l_{2,k}}\frac{\partial l_{2,k}}{\partial b_{2,k}}\\ =& \left(o_k-t_k\right)o_k\left(1-o_k\right)\end{array}$$

令

$${\delta }_k=\left(o_k-t_k\right)o_k\left(1-o_k\right)$$

• $L_k$关于隐藏层$l_1$权重系数$w_{1,ij}$的导数

$$\begin{array}{rl}\frac{\partial l_{1,j}}{\partial w_{1,ij}}=& x_i\\ \frac{\partial h_j}{\partial l_{1,j}}=& \frac{\partial \tanh (l_{1,j})}{\partial l_{1,j}}\\ =& \left(1-\tanh (l_{1,j})\right)\left(1+\tanh (l_{1,j})\right)\\ =& \left(1-h_j\right)\left(1+h_j\right)\\ \frac{\partial l_{2,k}}{\partial h_j}=& w_{2,jk}\end{array}$$

因此

$$\begin{array}{rl}\frac{\partial L_k}{\partial w_{1,ij}}=& \frac{\partial L_k}{\partial o_k}\frac{\partial o_k}{\partial l_{2,k}}\frac{\partial l_{2,k}}{\partial h_j}\frac{\partial h_j}{\partial l_{1,i}}\frac{\partial l_{1,i}}{\partial w_{1,ij}}\\ =& {\delta }_k{w}_{2,jk}\left(1-h_j\right)\left(1+h_j\right)x_i\end{array}$$

• $L_k$关于隐藏层$l_1$权重系数$b_{1,j}$的导数

$$\begin{array}{rl}\frac{\partial l_{1,j}}{\partial b_{1,j}}=& 1\end{array}$$

因此

$$\begin{array}{rl}\frac{\partial L_k}{\partial b_{1,j}}=& \frac{\partial L_k}{\partial o_k}\frac{\partial o_k}{\partial l_{2,k}}\frac{\partial l_{2,k}}{\partial h_j}\frac{\partial h_j}{\partial l_{1,i}}\frac{\partial l_{1,i}}{\partial b_{1,j}}\\ =& {\delta }_k{w}_{2,jk}\left(1-h_j\right)\left(1+h_j\right)\end{array}$$

• $L$关于隐藏层$l_2$权重系数$w_{2,jk}$的导数

$$\begin{array}{rl}\frac{\partial L}{\partial w_{2,jk}}=& \frac{\partial L_k}{\partial w_{2,jk}}=h_j{\delta }_k\end{array}$$

• $L$关于隐藏层$l_2$偏置系数$b_{2,k}$的导数

$$\begin{array}{rl}\frac{\partial L_k}{\partial b_{2,k}}=& \frac{\partial L_k}{\partial b_{2,k}}={\delta }_k\end{array}$$

• $L$关于隐藏层$l_1$权重系数$w_{1,ij}$的导数

$$\begin{array}{rl}\frac{\partial L}{\partial w_{1,ij}}=& \sum _k\frac{\partial L_k}{\partial w_{1,ij}}\\ =& \sum _k{\delta }_k{w}_{2,jk}\left(1-h_j\right)\left(1+h_j\right)x_i\\ =& \left(1-h_j\right)\left(1+h_j\right)x_i\sum _k{\delta }_k{w}_{2,jk}\end{array}$$

• $L$关于隐藏层$l_1$权重系数$b_{1,j}$的导数

$$\begin{array}{rl}\frac{\partial L}{\partial b_{1,j}}=& \sum _k\frac{\partial L_k}{\partial b_{1,j}}\\ =& \sum _k{\delta }_k{w}_{2,jk}\left(1-h_j\right)\left(1+h_j\right)\\ =& \left(1-h_j\right)\left(1+h_j\right)\sum _k{\delta }_k{w}_{2,jk}\end{array}$$

任务学习36: 神经网络数学原理（6）：手动演算神经网络BP算法（误差向后传递）

计算${\delta }_k$：

$${\delta }_k=\left(o_k-t_k\right)o_k\left(1-o_k\right)$$

$${\delta }_1=0.139707,{\delta }_2=-0.139707$$

import numpy as np

t = np.array([0, 1])
o = np.array([0.57, 0.43])

delta = (o - t) * o * (1 - o)

print("delta = {}".format(delta))

delta = [ 0.139707 -0.139707]

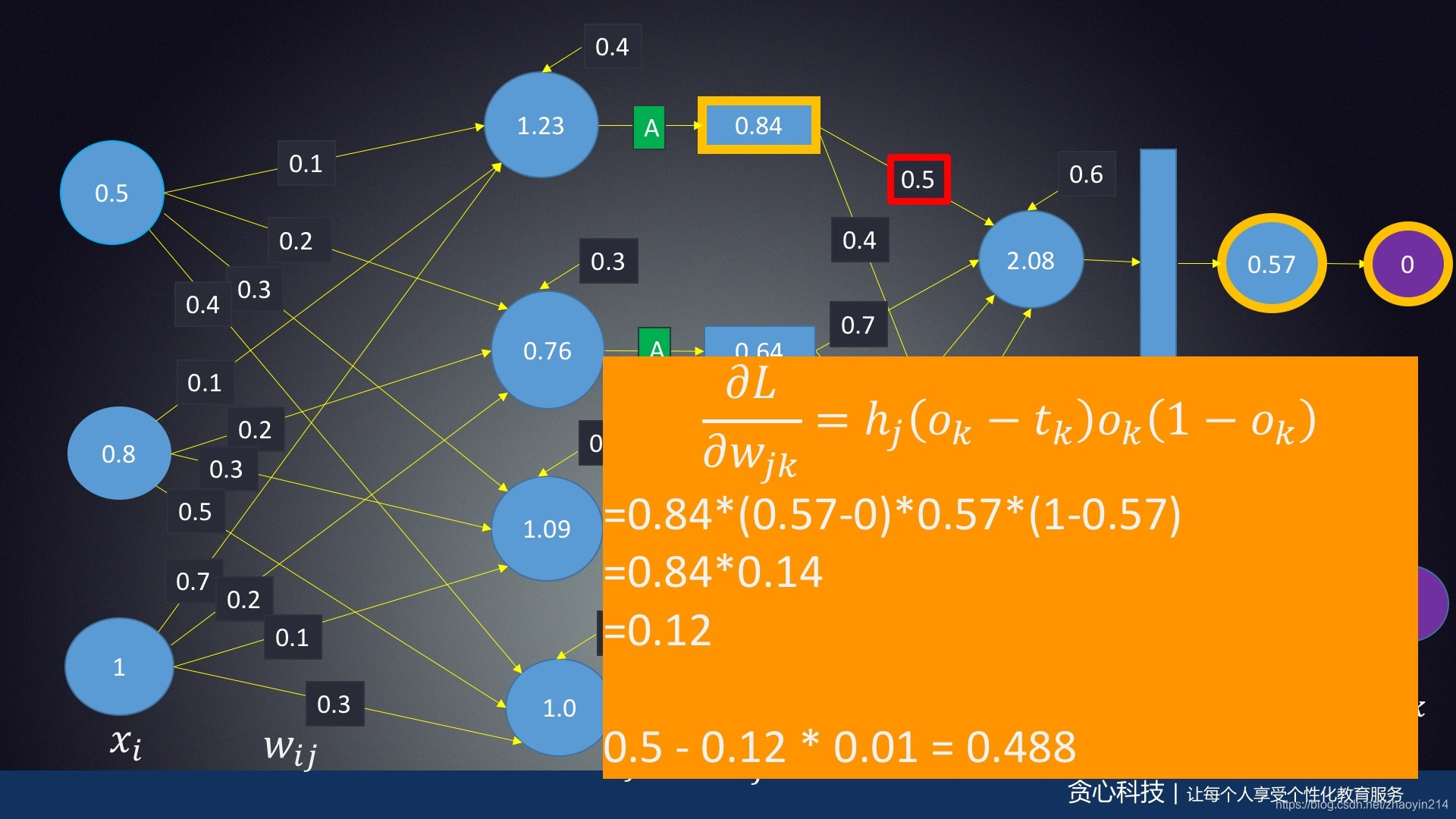
计算$\frac{\partial L}{\partial w_{2,11}}$，$\frac{\partial L}{\partial w_{2,12}}$：

$$\frac{\partial L}{\partial w_{2,jk}}=h_j{\delta }_k$$

$$\frac{\partial L}{\partial w_{2,11}}=h_1{\delta }_1=0.11735388,\frac{\partial L}{\partial w_{2,12}}=h_1{\delta }_2=-0.11735388$$

梯度下降

$$w_{2,jk}=w_{2,jk}-\alpha \frac{\partial L}{\partial w_{2,jk}}$$

$$\alpha =0.1,w_{2,11}=0.48826461,w_{2,12}=0.41173539$$

h = np.array([0.84, 0.64, 0.80, 0.76])

ploss_pw2 = np.dot(np.matrix(h).T, np.matrix(delta))
print("ploss_pw2 =\n {}".format(ploss_pw2))

alpha = 0.1

w2 = np.matrix([[0.5, 0.4], [0.7, 0.2], [0.1, 0.2], [0.7, 0.9]])

w2_new = w2 - alpha * ploss_pw2

print("w2 new =\n {}".format(w2_new))

ploss_pw2 =
 [[ 0.11735388 -0.11735388]
 [ 0.08941248 -0.08941248]
 [ 0.1117656  -0.1117656 ]
 [ 0.10617732 -0.10617732]]
w2 new =
 [[0.48826461 0.41173539]
 [0.69105875 0.20894125]
 [0.08882344 0.21117656]
 [0.68938227 0.91061773]]

任务学习37: 神经网络数学原理（7）：手动演算神经网络BP算法（误差向后传递）续

计算$\frac{\partial L}{\partial w_{1,11}}$：

$$\frac{\partial L}{\partial w_{1,ij}}=x_i\left[\left(1-h_j\right)\left(1+h_j\right)\sum _k{\delta }_k{w}_{2,jk}\right]$$

$$\frac{\partial L}{\partial w_{1,11}}=x_1\left[\left(1-h_1\right)\left(1+h_1\right)\sum _k{\delta }_k{w}_{2,1k}\right]=0.00205649$$

梯度下降

$$w_{1,ij}=w_{1,ij}-\alpha \frac{\partial L}{\partial w_{1,ij}}$$

$$\alpha =0.1,w_{1,11}=0.09979435$$

x = np.array([0.5, 0.8, 1])

w2_dot_delat = np.dot(w2, np.matrix(delta).T).T.A

vec_j = (1 - h) * (1 + h) * w2_dot_delat

ploss_pw1 = np.dot(np.matrix(x).T, np.matrix(vec_j))

print("ploss_pw1 =\n {}".format(ploss_pw1))

w1 = np.matrix([[0.1, 0.2, 0.3, 0.4], [0.1, 0.2, 0.3, 0.5], [0.7, 0.2, 0.1, 0.3]])

w1_new = w1 - alpha * ploss_pw1

print("w1 new =\n {}".format(w1_new))

ploss_pw1 =
 [[ 0.00205649  0.02062075 -0.00251473 -0.00590122]
 [ 0.00329038  0.03299321 -0.00402356 -0.00944196]
 [ 0.00411297  0.04124151 -0.00502945 -0.01180245]]
w1 new =
 [[0.09979435 0.19793792 0.30025147 0.40059012]
 [0.09967096 0.19670068 0.30040236 0.5009442 ]
 [0.6995887  0.19587585 0.10050295 0.30118024]]