codeforces 1016D. Vasya And The Matrix

链接

提议很简单，就是一个矩阵，你知道每行，每列异或后的结果，然后还原这个矩阵，如果不能还原输出NO。

很显然这是一个构造，比赛时没有想出来，真是有点傻。。但是看了好多博客发现大家都是简单的写个结论，什么全补0，只保留最后一行，一列。几乎没有解释为什么这样的。我把自己的理解写出吧。

对于这个矩阵:
a1 = x1^x2x3,a2 = x4^x5x6;
b1 = x1^x4,b2 = x2^x5,b3 = x3^x6;
所以a1^a2 = x1^x2x3^x4x5^x6;
b1^b2b3 = x1^x2x3^x4x5^x6;
所以行列异或值是否相等，或者二者再异或结果为0，就是判断是否有解的条件来。
对于有解的情况我们仍要构造出一种矩阵，我们可以只考虑最后一行，一列空的做法。也可以逐位枚举来计算。
我们如果把前面都填上一样的数，这样最后一列数也可以确定下来，因为0异或任何数结果还是那个数，所以我们一般是填0，
这样的话，这个矩阵就是如下

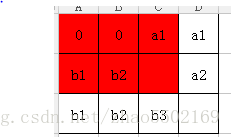
这样空白的那个空就是b1^b2a2求得，或者是a1^b3求得。这样填一定符合吗？我们首先来