深度学习中的模型选择与过拟合缓解策略-优快云博客

本文链接：https://blog.youkuaiyun.com/zhangyugebb/article/details/101123316

本文探讨了模型选择中的验证数据集和k折交叉验证，以及欠拟合和过拟合的概念。过拟合发生在训练误差低但测试误差高的情况下，可以通过权重衰减（L2范数正则化）和丢弃法来缓解。权重衰减通过增加损失函数惩罚项减少模型复杂度，丢弃法则在训练过程中随机忽略部分神经元以防止过拟合。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

训练误差（training error）：模型在训练数据集上表现出的误差。

泛化误差（generalization error）：模型在任意一个测试数据样本上表现出的误差的期望，常常通过测试数据集上的误差来近似。

机器学习模型应该关注泛化误差。

模型选择（model selection）

1. 验证数据集（validation set）：预留一部分在训练数据集和测试数据集以外的数据进行模型选择，例如我们可以从给定的训练集中选取一小部分作为验证集，剩余部分作为真正的训练集。

2. k折交叉验证（k-fold cross-validation）：由于验证数据集不参与模型训练，当训练数据不够用时，预留大量的验证数据显得太奢侈，并且人们发现用同一数据集，既进行训练，又进行模型误差估计，对误差估计的很不准确，这就是所说的模型误差估计的乐观性。为了克服这个问题，提出了交叉验证：我们把训练数据集分割成k个不重合的子数据集，然后我们做k次模型训练和验证。每一次我们使用一个子数据集验证模型，并使用其他k-1个子数据集来训练模型。最后，我们对这k次训练误差和验证误差分别求平均。

欠拟合和过拟合

欠拟合（underfitting)：模型无法得到较低的训练误差。

过拟合(overfitting)：模型的训练误差远小于其在测试集上的误差。

造成过拟合和欠拟合的主要原因是模型复杂度和训练数据集的大小。

模型复杂度：

1. 给定训练数据集，如果模型的复杂度过低，很容易出现欠拟合。

2. 如果模型的复杂度过高，容易出现过拟合。

训练数据集大小：

一般来说，训练数据集中样本过少（特别是比模型参数数量更少时），过拟合更容易发生。

测试如下：

1. 正常拟合，虽然这里测试集上的误差比训练误差还好

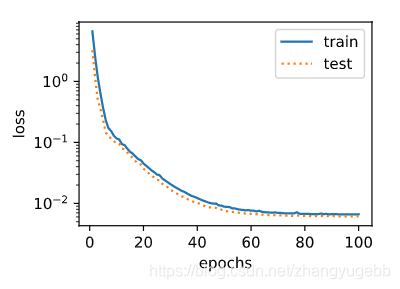
2. 欠拟合，训练集误差很大，并且训练误差在迭代早期下降后就很难继续降低。（这里选择了一个低阶模型去拟合高阶模型产生的数据）

3. 过拟合，训练误差很小，测试集上的误差很大。（这里使用少量的数据去训练模型）

应对过拟合的常用方法：

权重衰减（weight decay）

权重衰减也叫L2范数正则化（regularization）。通过为模型的损失函数添加惩罚项使学出的模型参数值较小。带有L2范数惩罚项的新损失函数为：

$l(\boldsymbol{w},\boldsymbol{b})+\frac{\lambda }{2n}\left \| \boldsymbol{w} \right \|^2$

即

$\frac{1}{n}\sum_{i=1}^{n}\frac{1}{2}(\hat{y}^{(i)}-y^{(i)})^2+\frac{\lambda }{2n}\left \| \boldsymbol{w} \right \|^2$

其中权重衰减超参数 $\lambda$ > 0。当权重参数 w 均为0时，惩罚项最小。当 $\lambda$ 较大时，惩罚项在损失函数中的比重较大，这通常会使学到的权重参数的元素较接近0。

PS：正则化（regularization）按照个人理解是给模型加上约束（惩罚），用于降低模型的复杂度。

MXNet实现：

这里我们直接在构造Trainer实例时通过wd参数来指定权重衰减超参数。默认下，Gluon会对权重和偏差同时衰减。我们可以分别对权重和偏差构造Trainer实例，从而只对权重衰减。

%matplotlib inline
import d2lzh as d2l
from mxnet import autograd, gluon, nd
from mxnet.gluon import data as gdata, loss as gloss, nn

def fit_and_plot_gluon(wd):
    """wd即为上式中的lambd值"""
    net = nn.Sequential()
    net.add(nn.Dense(1))
    net.initialize(init.Normal(sigma=1))
    # 对权重参数衰减。权重名称一般是以weight结尾
    trainer_w = gluon.Trainer(net.collect_params('.*weight'), 'sgd',
                              {'learning_rate': lr, 'wd': wd})
    # 不对偏差参数衰减。偏差名称一般是以bias结尾
    trainer_b = gluon.Trainer(net.collect_params('.*bias'), 'sgd',
                              {'learning_rate': lr})
    train_ls, test_ls = [], []
    for _ in range(num_epochs):
        for X, y in train_iter:
            with autograd.record():
                l = loss(net(X), y)
            l.backward()
            # 对两个Trainer实例分别调用step函数，从而分别更新权重和偏差
            trainer_w.step(batch_size)
            trainer_b.step(batch_size)
        train_ls.append(loss(net(train_features),
                             train_labels).mean().asscalar())
        test_ls.append(loss(net(test_features),
                            test_labels).mean().asscalar())
    d2l.semilogy(range(1, num_epochs + 1), train_ls, 'epochs', 'loss',
                 range(1, num_epochs + 1), test_ls, ['train', 'test'])
    print('L2 norm of w:', net[0].weight.data().norm().asscalar())

fit_and_plot_gluon(0)
fit_and_plot_gluon(3)

丢弃法（dropout）

在训练过程中对隐藏层的神经元进行丢弃的方法，可以使输出层的计算无法过度依赖某一个神经元，从而在训练模型的时候起到正则化的作用。

注意，这里只是在训练过程中使用丢弃法进行计算。

设丢弃概率为 p ，那么有 p 的概率 $h_i$ (隐藏神经元)会被清零，有 1-p 的概率 $h_i$ 会除以 1-p 做拉伸。丢弃概率是丢弃法的超参数。

使用丢弃法计算新的隐藏单元：

$h_i^{'} = \frac{\xi_i }{1-p}h_i$

由于 $E(\xi _i) = 1-p$ ，因此：

$E(h_i^{'}) = \frac{E(\xi_i) }{1-p}h_i = h_i$

即丢弃法不会改变隐藏层的期望值。

使用MXNet实现：

import d2lzh as d2l
from mxnet import autograd, gluon, init, nd
from mxnet.gluon import loss as gloss, nn

"""定义dropout函数，drop_prob为丢弃概率，即使用概率drop_prob对X中的元素清零"""
def dropout(X, drop_prob):
    # assert作用，其条件为假，则终止程序
    assert 0 <= drop_prob <= 1
    keep_prob = 1 - drop_prob
    # 这种情况下把全部元素都丢弃
    if keep_prob == 0:
        return X.zeros_like()
    # 在[0，1]上均匀分布的<keep_prob的mask
    mask = nd.random.uniform(0, 1, X.shape) < keep_prob
    return mask * X / keep_prob

# 定义模型参数
num_inputs, num_outputs, num_hiddens1, num_hiddens2 = 784, 10, 256, 256
W1 = nd.random.normal(scale=0.01,shape=(num_inputs, num_hiddens1))
b1 = nd.zeros(num_hiddens1)
W2 = nd.random.normal(scale=0.01,shape=(num_hiddens1, num_hiddens2))
b2 = nd.zeros(num_hiddens2)
W3 = nd.random.normal(scale=0.01,shape=(num_hiddens2, num_outputs))
b3 = nd.zeros(num_outputs)
params = [W1,b1,W2,b2,W3,b3]
for param in params: # 添加需要求导的参数
    param.attach_grad()

# 定义模型
drop_prob1, drop_prob2 = 0.2, 0.5
def net(X):
    X = X.reshape((-1, num_inputs))
    H1 = (nd.dot(X,W1)+b1).relu()
    if autograd.is_training():  # 只在模型训练的时候丢弃
        H1 = dropout(H1, drop_prob1)
    H2 = (nd.dot(H1,W2)+b2).relu()
    if autograd.is_training():  
        H2 = dropout(H2, drop_prob2)
    return nd.dot(H2, W3)+b3

# 训练和测试模型
num_epochs, lr, batch_size = 5, 0.5, 256
loss = gloss.SoftmaxCrossEntropyLoss()
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, batch_size, params, lr)

-----------------------------------------------------------------------------------------------
"""简洁实现"""
net = nn.Sequential()
net.add(nn.Dense(256, activation='relu'),
       nn.Dropout(drop_prob1),
       nn.Dense(256,activation='relu'),
       nn.Dropout(drop_prob2),
       nn.Dense(10))
net.initialize(init.Normal(sigma=0.01))

trainer = gluon.Trainer(net.collect_params(), 'sgd', {'learning_rate':lr})
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, batch_size, None, None, trainer)

# 直接使用MXNet的函数实现相对于手动实现的优点：
# 1.不需要手动定义以及初始化权重参数和偏差值
# 2.简洁的模型构建

Reference：

《动手学深度学习》-Aston Zhang