CS224W 13 Community Detection in Networks

目录

13.1 Community Detection in Networks ——直观解释

信息如何在网络中流动(以社交网络为例)

社区如何形成？

Edge Overlap

13.2 Network Communities

定义

Modularity

13.3 Louvain Algorithm

13.4 Detecting Overlapping Communities

Community- Affiliation Graph Model(AGM)

使用AGM检测社区

思路

Graph Likelihood P(G|F）——计算F生成G的可能性

"Relaxing" AGM: Towards P(u,v)——扩展AGM以说明成员优势

 BigCLAM Model

13.1 Community Detection in Networks ——直观解释

Community Detection本质上是对图中的一组节点进行集群(基于网络结构)。社区内边比社区间边多。

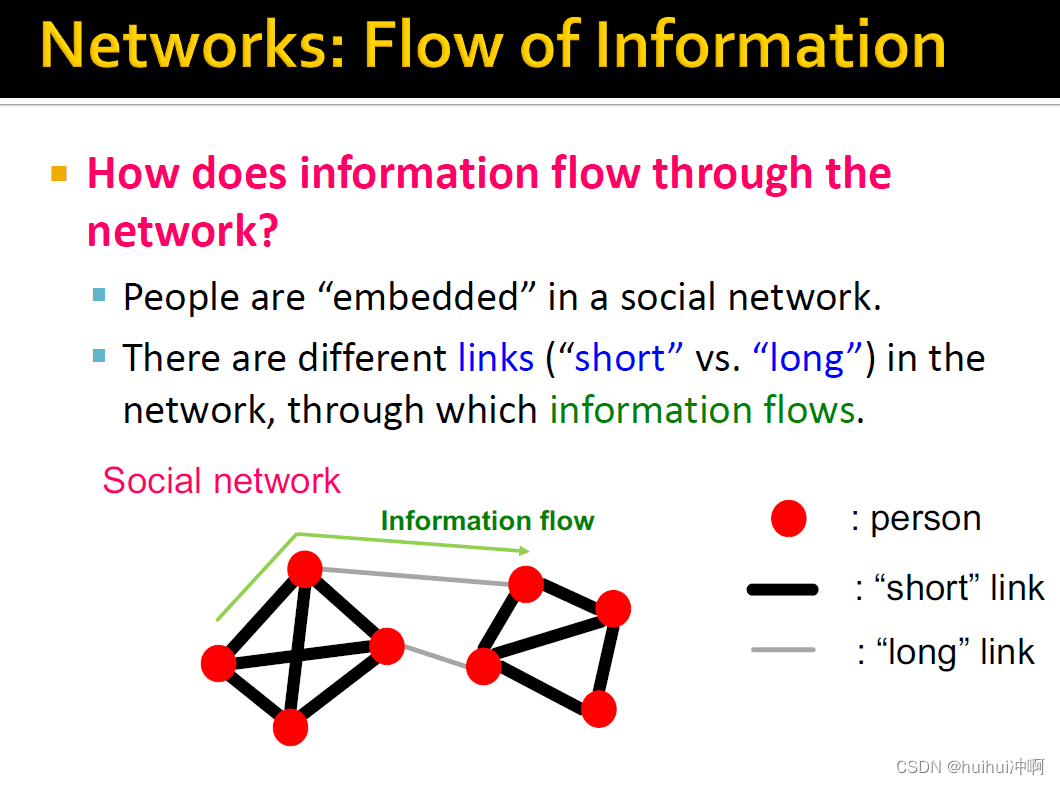
信息如何在网络中流动(以社交网络为例)

1.人被嵌到网络中的节点上。信息通过不同的边流动(short：两个人联系很紧密 long:两人联系很弱)

 2.有研究表明找工作时，是通过weak连接的熟人找到的，而不是那些强连接的亲密朋友，为什么？

Granovetter's Answer

• 对友谊(链接)的两种观点：

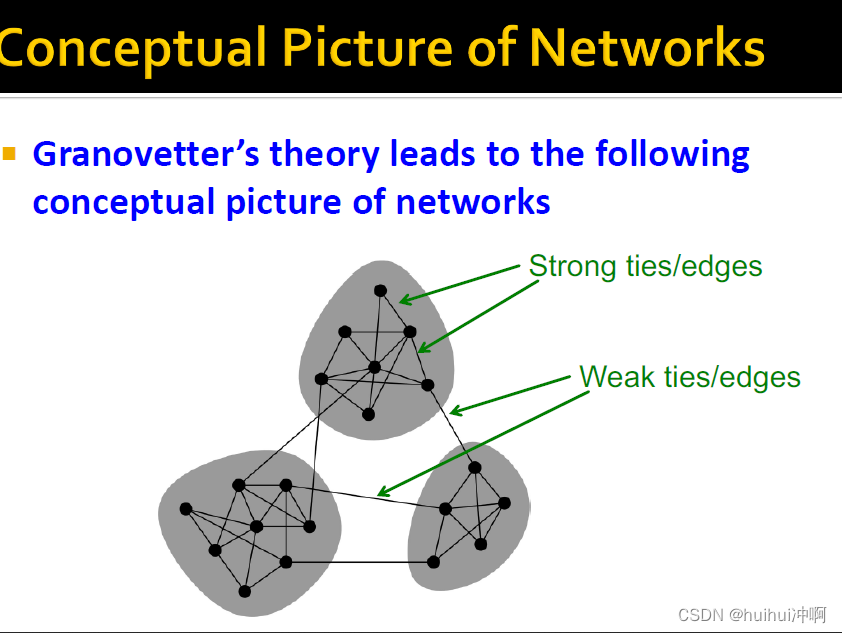
        边的Structural结构性作用。社区间边连接网络不同部分。社区内边很好的嵌入在网络内部，拥有共同好友建立非常紧密的关系。

        interpersonal(人际关系)。两个人之间的关系是strong还是weak

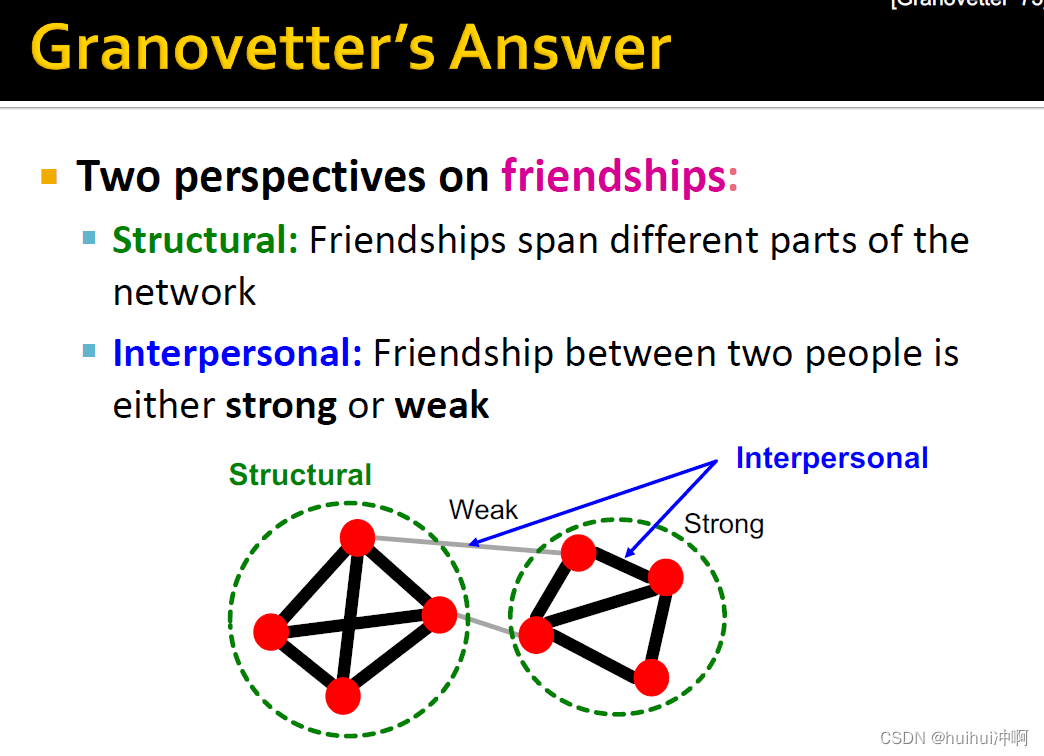
• Granovetter建立了边的social 和 structural作用的联系
• 第一种观点Structure
  • structural embedded(紧密连接)的边socially strong，有很多紧密联系的人，结构性很强。
  • 连接不同部分的远程边socially weak
• 第二种观点Information
  • 远程边可以让你聚集网络不同部分的信息
  • structural embedded 边则在信息获取上有很重的冗余(你朋友都和你有直接联系的边，谁知道工作可以直接告诉你，那这个工作信息在通过其他朋友的其他边传播就没用了)

社区如何形成？

社区倾向于使用Triadic Closure(三重闭合)来形成：因为如果网络中的两个人有个共同好友，那么他们二人也很可能成为朋友。

1.Triadic Closure

 Triadic Closure的度量通过聚类系数度量。

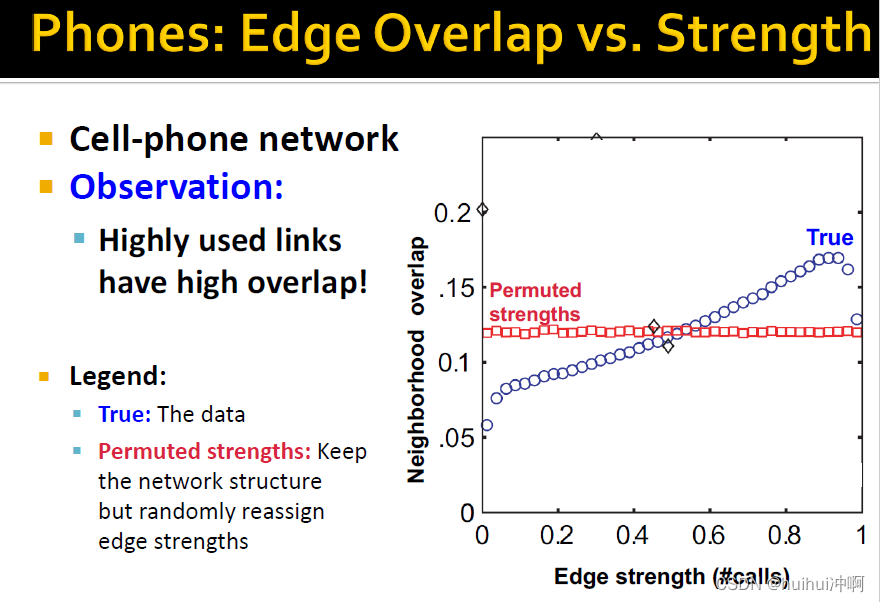
Edge Overlap

边在结构上的weak strong可以用Edge Overlap的概念来量化。描述边的端点共有多少邻居。

是边的两个端点i和j除了自身外 共有的邻居节点数➗两者邻居节点数之和。越高，连接越强

 从图中看出，越高的overlap，边使用的频率越高，电话数量会越多。

基于strength移除边。如果移除weak边(连接网络不同部分)，断开网络连接的速度很快；如果移除strong边(嵌入网络集群中，使用频率会很高)，也不一定会断开网络连接，因此速度慢。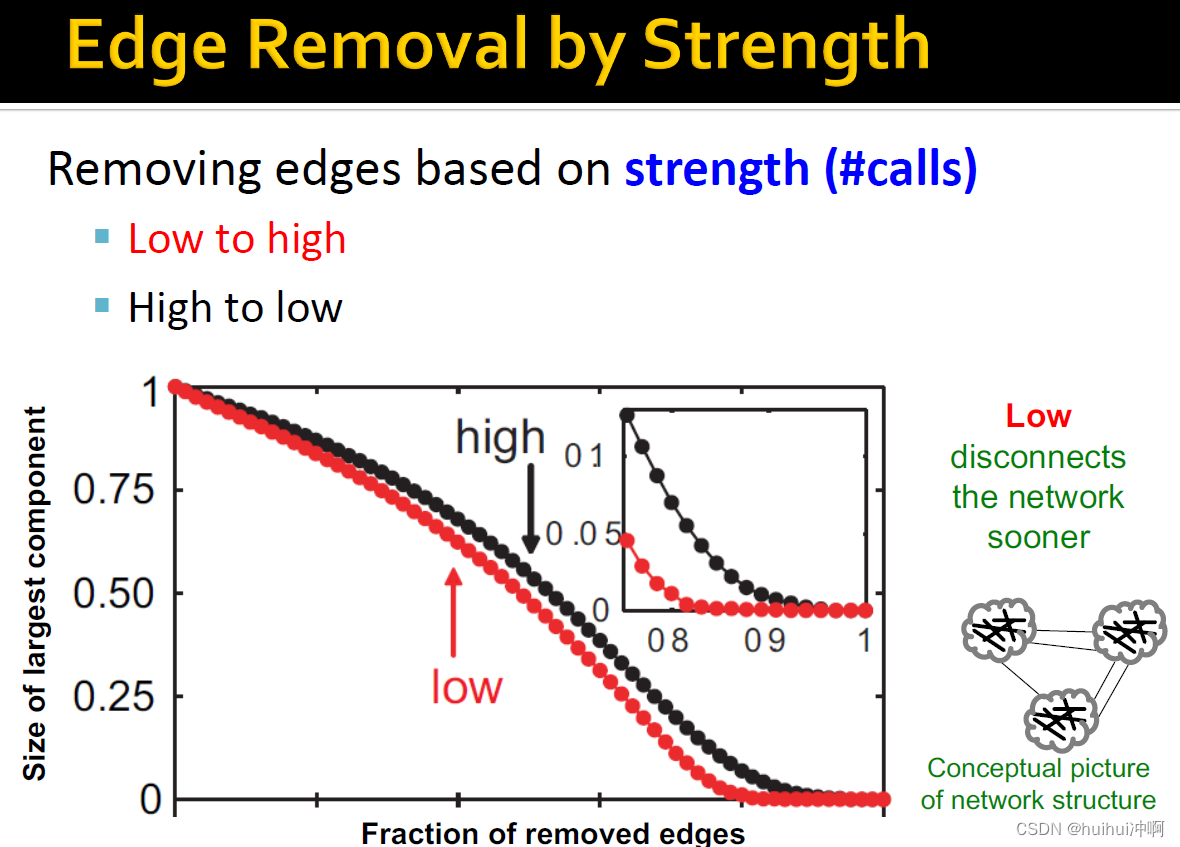

 基于edge overlap移除边。如果移除低overlap的边，断开网络连接的速度很快

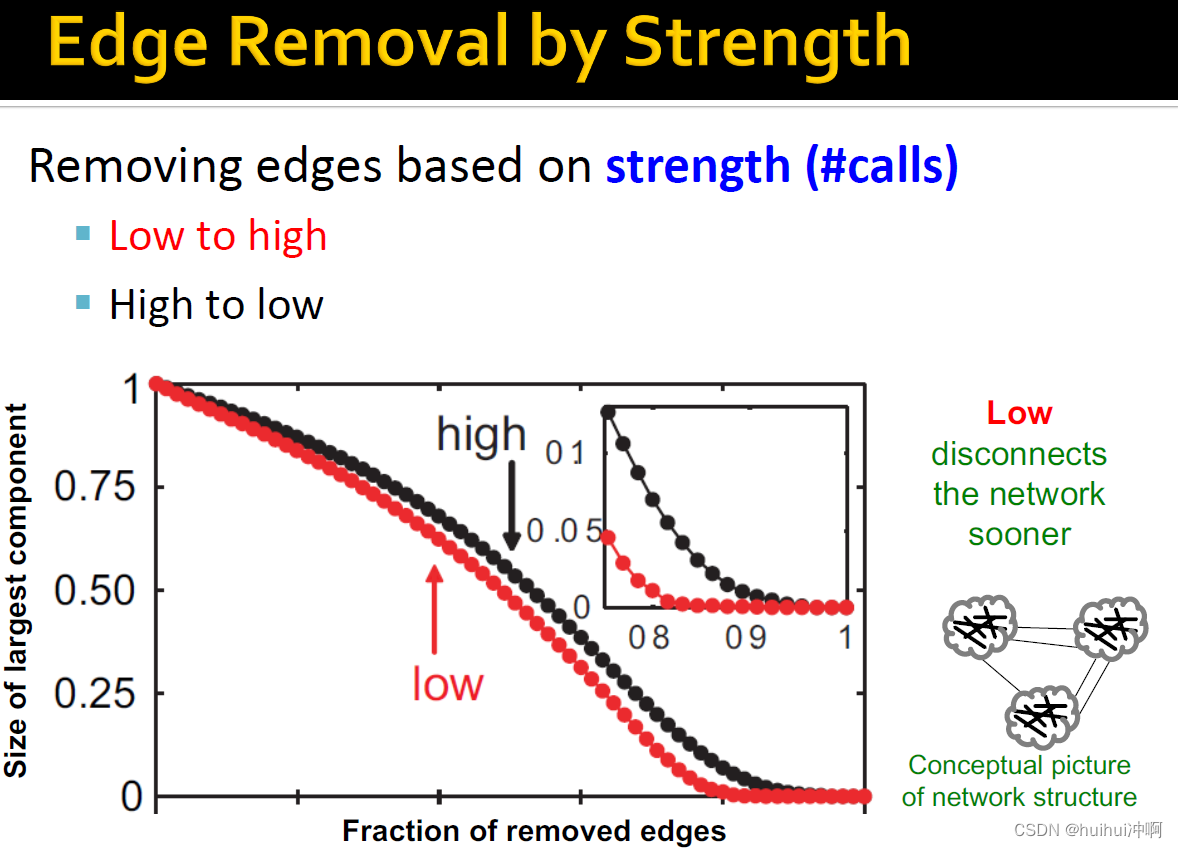
 interpersonal strength 是高overlap，embedding在网络中，有很强的联系；低或者零overlap的边，连接网络不同部分，往往weak

13.2 Network Communities

定义

网络是由紧密连接的多个节点集构成的。

网络社区的概念：节点集具有大量内部连接和少量的外部连接(和网络其他部分的连接)

如何自动找到紧密连接的节点组？理想上紧密连接的节点组和真实的节点组相对应。

Modularity

1.定义

模块化衡量网络被多好的划分为社区。

目标：找到一组分区是模块化程度尽可能高。

 Q =  每个小组s内边的个数和期望的null model的小组s内边个数的差，再对所有小组求和。

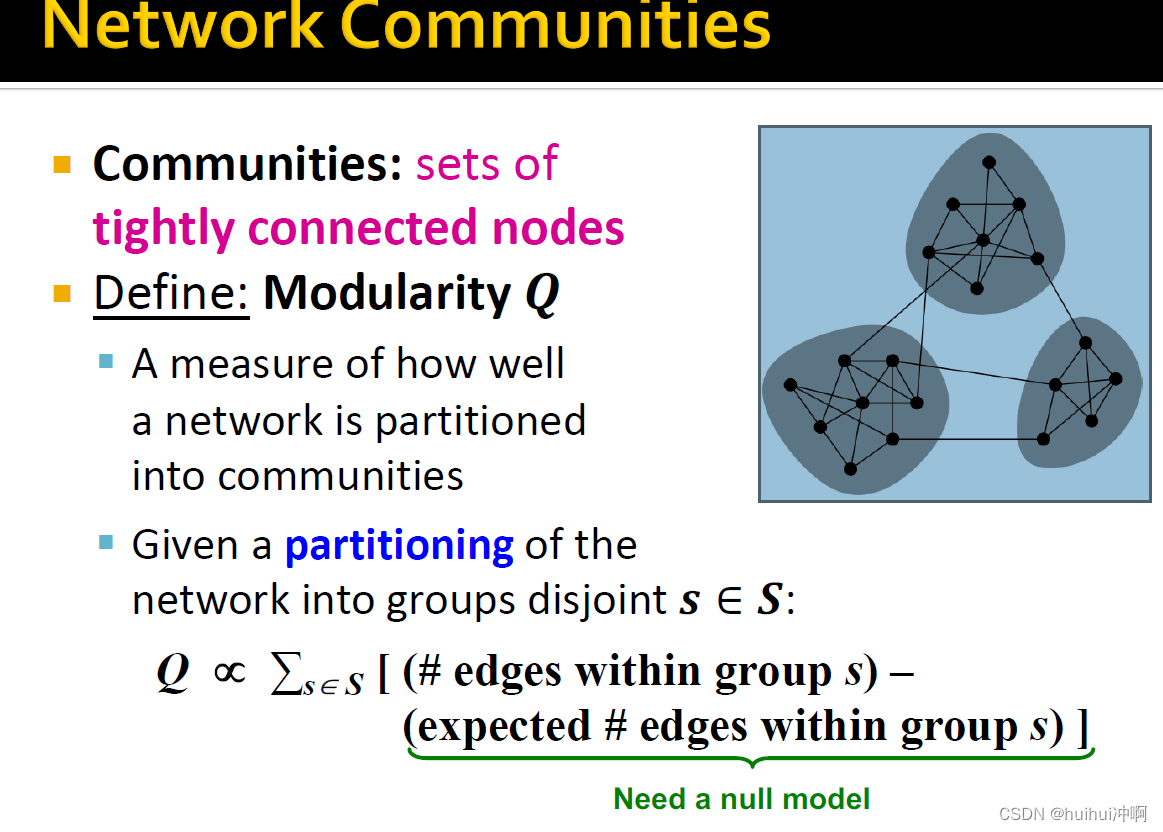
2.null modlel