递归

在实现链表的反转的时候可以用到递归算法的方式

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
    public ListNode reverseList(ListNode head) {
        //递归退出的条件，当当前结点为null或者next为null
        if(head==null||head.next==null){
            return head;
        }
        //进入递归
        ListNode newHead=reverseList(head.next);
         //先将node进行逆转
        // ListNode temp =head.next;
        // temp.next=head;
        head.next.next=head;
        //进行断链操作
        head.next=null;
        return newHead;
    }
}

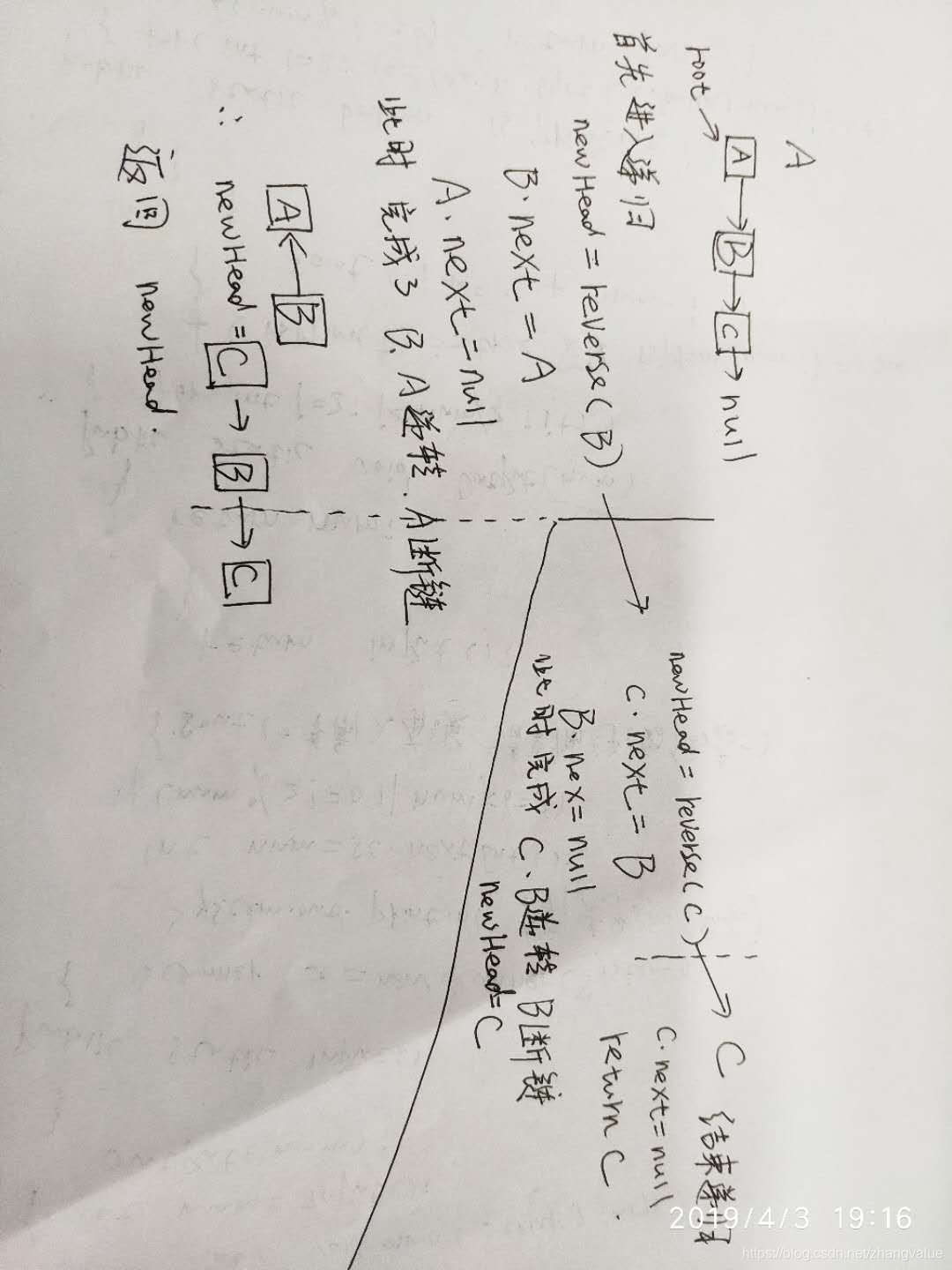
可以画出链表反转的过程，如下图：

1.何为递归

个人理解就是自己调用自己，直到满足一个条件结束自己调用自己的过程，这个就是递归。举一个通俗的点的例子：

假设你在一个电影院，你想知道自己坐在哪一排，但是前面人很多，你懒得去数了，于是你问前一排的人「你坐在哪一排？」，这样前面的人 (代号 A) 回答你以后，你就知道自己在哪一排了——只要把 A 的答案加一，就是自己所在的排了，不料 A 比你还懒，他也不想数，于是他也问他前面的人 B「你坐在哪一排？」，这样 A 可以用和你一模一样的步骤知道自己所在的排。然后 B 也如法炮制，直到他们这一串人问到了最前面的一排（或者说问到了知道自己是哪一排的人，预示着调用结束），第一排的人告诉问问题的人「我在第一排」，最后大家就都知道自己在哪一排了
 

2.递归算法设计的基本思想是：

对于一个复杂的问题，把原问题分解为若干个相对简单类同的子问题，继续下去直到子问题简单到能够直接求解，也就是说到了递推的出口，这样原问题就有递推得解。 
关键要抓住的是： 
（1）递归出口 
（2）地推逐步向出口逼近 

3.常见递归算法

（1）最常见的就是阶乘，比如求5的阶乘，数学公式就是：5*4*3*2*1，代码：

public static int digui(int n) {
        if (n == 1 || n == 0) {
            return n;
        } else {
            return n * digui(n - 1);
        }
    }

（2）求1+2+3+4+5+6+7……+1000的和

 /**
     * 递归调用（累加）求1+2+3+4+5+6+7……+1000的和
     *
     * @param i
     * @return
     */
    public static int count(int i) {
        if (i > 0) {
            return i + count(i - 1);
        } else {
            return 0;
        }
    }

（3）1,1,2,3,5,8,13,21,34...，求用递归算第30个数

 /**
     * 斐波拉契数列
     * 1,1,2,3,5,8,13,21,34...，求用递归算第30个数
     *
     * @return
     */
    public static int Fibonaccisequence(int n) {
        if (n == 1 || n == 2) {
            return 1;
        } else {
            return Fibonaccisequence(n - 1) + Fibonaccisequence(n - 2);
        }
    }