递归画美图，你可以做到

于 2013-11-25 20:05:44 发布
阅读量488 收藏 3
点赞数
分类专栏： Java基础 文章标签： java

       在算法中有一种很好的方法叫递归，他在程序设计中应用广泛。

       递归算法解决问题的特点：

　　(1) 递归就是在过程或函数里调用自身。

　　(2) 在使用递归策略时，必须有一个明确的递归结束条件，称为递归出口。

　　(3) 递归算法解题通常显得很简洁，但递归算法解题的运行效率较低。所以一般不提倡用递归算法设计程序。

　　(4) 在递归调用的过程当中系统为每一层的返回点、局部量等开辟了栈来存储。递归次数过多容易造成栈溢出等。所以一般不提倡用递归算法设计程序。

       递归算法的要求：

　　递归算法所体现的“重复”一般有三个要求：

　　一是每次调用在规模上都有所缩小(通常是减半)；

　　二是相邻两次重复之间有紧密的联系，前一次要为后一次做准备(通常前一次的输出就作为后一次的输入)；

　　三是在问题的规模极小时必须用直接给出解答而不再进行递归调用，因而每次递归调用都是有条件的(以规模未达到直接解答的大小为条件)，无条件递归调用将会成为死循环而不能正常结束。

         以上的内容基本来自百度，我感觉递归就两个特点：自身调用自身，要有一个出口函数。

         下面进入主题，本篇博客是要说的是用递归的方法来绘制美丽的图像，真的很美丽你可以尝试一下，一共两个程序。给大家抛个砖，你可以画出更美丽的图像。

         第一个是用递归的方法画出美丽的树枝：代码如下，有注释：

import java.awt.BorderLayout;
import java.awt.Color;
import java.awt.Dimension;
import java.awt.Graphics;
import java.awt.Graphics2D;
import java.awt.Toolkit;
import java.awt.event.ActionEvent;
import java.awt.event.ActionListener;
import java.util.Random;

import javax.swing.JButton;
import javax.swing.JFrame;
import javax.swing.JPanel;
import javax.swing.UIManager;
import javax.swing.UnsupportedLookAndFeelException;
 
public class GraphicsTest extends JFrame implements ActionListener { 
    public static final double PI = Math.PI / 180; 
    JPanel panel; 
    JPanel pnlCtl; 
    JButton button; 
    JButton button2; 
    Graphics2D g2; 
 
    public GraphicsTest(String string) { 
        super(string); 
    } 
 
    public void init() { 
       
    	//面板panel用来画图，设置背景为黑色，更能体现出树的美丽
    	panel = new JPanel(); 
        panel.setBackground(Color.black);
       
        //面板panel2用来放置控制按钮
        JPanel panel2 = new JPanel(); 
        button = new JButton("美树"); 
        button2 = new JButton("清除"); 
        this.add(panel, BorderLayout.CENTER); 
        button.addActionListener(this); 
        button2.addActionListener(this); 
        panel2.setBackground(Color.green);
        panel2.add(button); 
        panel2.add(button2); 
        this.add(panel2, BorderLayout.NORTH); 
        setSize(800, 600); 
        this.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE); 
        this.setVisible(true); 
        Dimension winSize = Toolkit.getDefaultToolkit().getScreenSize(); 
        this.setLocation((winSize.width - this.getWidth()) / 2, 
                (winSize.height - this.getHeight()) / 2); 
        g2 = (Graphics2D) panel.getGraphics(); 
    } 
 
    public static void main(String[] args) throws ClassNotFoundException, 
        InstantiationException, IllegalAccessException, 
        UnsupportedLookAndFeelException { 
        UIManager.setLookAndFeel(UIManager.getSystemLookAndFeelClassName()); 
        GraphicsTest testPanel = new GraphicsTest("美丽的分形"); 
        testPanel.init(); 
    } 
 
     
    @Override 
    public void actionPerformed(ActionEvent e) { 
        if ("美树".equals(e.getActionCommand())) { 
            drawLeaf(g2, 400, 500, 100, 210+random.nextInt(100)); 
        } else if ("清除".equals(e.getActionCommand())) { 
        	panel.getGraphics().setColor(Color.black);
        	panel.getGraphics().fillRect(0, 0, 800, 800);
        } 
    } 
    Random random=new Random(); 
    public void  drawLeaf(Graphics g, double x, double y, double L, double a) { 
       
        int red = random.nextInt(127); 
        int green = random.nextInt(127); 
        int blue = random.nextInt(127); 
        //随机颜色 
        g.setColor(new Color(red, green, blue)); 
        double x1, x2, x1L, x2L, x2R, x1R, y1, y2, y1L, y2L, y2R, y1R; 
       
        //侧干主干的夹角 
        float deflection = 50-random.nextInt(20);
        //主干偏转角度 
        float intersection = random.nextInt(40)-20; 
        //限制递归深度 
        float depth = 2+random.nextInt(2);
        //主干侧干长度比(可调整使其更茂密或稀疏) 
        float ratio = 3f;
        
        //上级主干与本级主干长度比（可调整使其变高低） 
        float ratio2 = 1.2f;
        if (L > depth) { 
            x2=x+L*Math.cos(a*PI); 
            y2=y+L*Math.sin(a*PI); 
            x2R=x2+L/ratio*Math.cos((a+deflection)*PI); 
            y2R=y2+L/ratio*Math.sin((a+deflection)*PI); 
            x2L=x2+L/ratio*Math.cos((a-deflection)*PI); 
            y2L=y2+L/ratio*Math.sin((a-deflection)*PI); 
            x1=x+L/ratio*Math.cos(a*PI); 
            y1=y+L/ratio*Math.sin(a*PI); 
            x1L=x1+L/ratio*Math.cos((a-deflection)*PI); 
            y1L=y1+L/ratio*Math.sin((a-deflection)*PI); 
            x1R=x1+L/ratio*Math.cos((a+deflection)*PI); 
            y1R=y1+L/ratio*Math.sin((a+deflection)*PI); 
            g.drawLine((int)x,(int)y,(int)x2,(int)y2); 
            g.drawLine((int)x2,(int)y2,(int)x2R,(int)y2R); 
            g.drawLine((int)x2,(int)y2,(int)x2L,(int)y2L); 
            g.drawLine((int)x1,(int)y1,(int)x1L,(int)y1L);   
            g.drawLine((int)x1,(int)y1,(int)x1R,(int)y1R); 
           
            //递归调用
            drawLeaf(g,x2,y2,L/ratio2,a+intersection); 
            drawLeaf(g,x2R,y2R,L/ratio,a+deflection); 
            drawLeaf(g,x2L,y2L,L/ratio,a-deflection); 
            drawLeaf(g,x1L,y1L,L/ratio,a-deflection); 
            drawLeaf(g,x1R,y1R,L/ratio,a+deflection); 
        } 
    } 
}

   运行如下：

 

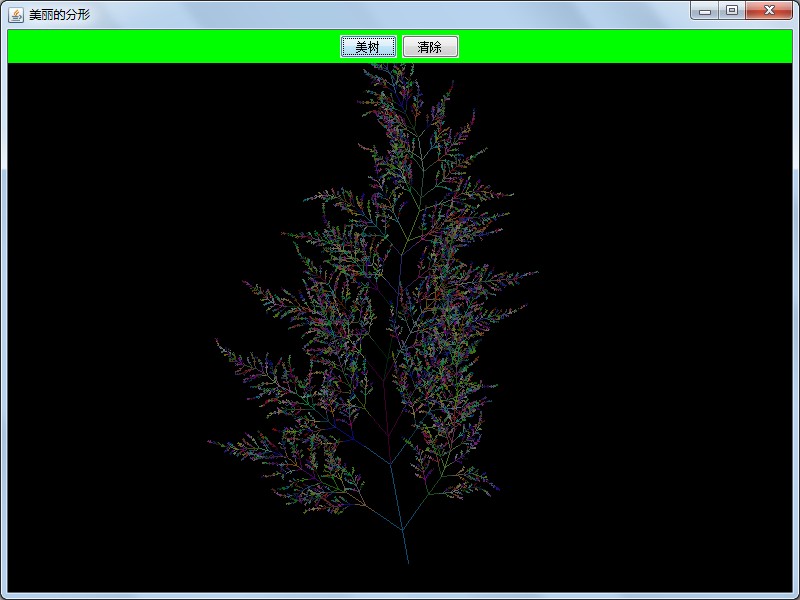
 多画几支，你会发现他很像孔雀开的屏：



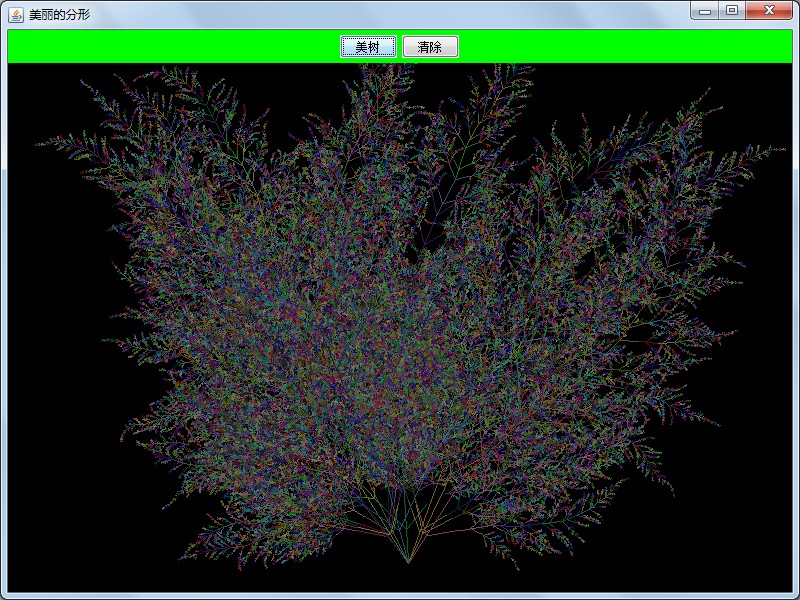
 是不是很漂亮，你可以改改代码做出更美丽的图。

 

 

 

 

下面是也是应用递归画出的一个，这个叫做“神奇的色子”具体的要求如下：

1.平面上随机选A,B,C三个点。再随机选一个点，记为P。
2.有一个三面色子，每丢一次，则选中ABC三个中一点。
开始游戏：
1.重复丢色子，如果选中A，则取A和P的中点P1，画黑，
2.如果选中B，则取B和P1的中点P2，画黑
3.如果选中A，则取A和P2的中点P3，画黑
4….一直重复（如每点一下鼠标，丢100次色子。）

当你按要求继续下去的时候你会发现出现很神奇的一幕不多说代码如下：（有注释）

package 神奇的色子;

import java.awt.Color;
import java.awt.FlowLayout;
import java.awt.Graphics;
import java.awt.event.ActionEvent;
import java.awt.event.ActionListener;
import java.util.Random;

import javax.swing.JButton;
import javax.swing.JFrame;

public class Drawsezi extends JFrame implements ActionListener{
	
	//入口函数
	public static void main(String[] args) {
		Drawsezi se = new Drawsezi();
		se.init();
	}
	
	//设置画图板
	public void init() {
		
		//初始化画板
		this.setSize(600, 600);
		this.setDefaultCloseOperation(3);
		this.setLayout(new FlowLayout());
		this.setLocationRelativeTo(null);
		this.getContentPane().setBackground(Color.black);
		this.setVisible(true);
		
		//获取画布对象
		 g =this.getGraphics();
		
		 //添加一个控制按钮
		JButton bu = new JButton("画图");
		//bu.setActionCommand("draw");
		this.add(bu);
		bu.addActionListener(this);
	}
	
	//产生四个点的随机数10--999,防止点在画布外面
	Random r = new Random();
    int Ax = r.nextInt(700)+10;
    int Ay = r.nextInt(700)+10;
    int Bx = r.nextInt(700)+10;
    int By = r.nextInt(700)+10;
    int Cx = r.nextInt(700)+10;
    int Cy = r.nextInt(700)+10;
    int Dx = r.nextInt(700)+10;
    int Dy = r.nextInt(700)+10;
    int Ex = r.nextInt(700)+10;
    int Ey = r.nextInt(700)+10;
    int Px = r.nextInt(700)+10;
    int Py = r.nextInt(700)+10;
    
	
	//重写ActionListener的方法
    public void actionPerformed(ActionEvent e) {
      
        for(int i = 0; i < 10000; i++) {    
            int m = r.nextInt(5);     //产生随机数0,1,2,4对应A,B,C,D
          if(m == 0) {                //选中A
        	  Px = (Ax+Px)/2;
        	  Py = (Ay+Py)/2;
        	  g.setColor(new Color(50,230,0));
        	  g.drawLine(Px, Py, Px, Py);
        	  
          } else if(m == 1) {          //选中B
        	  Px = (Bx+Px)/2;
        	  Py = (By+Py)/2;
        	  g.setColor(new Color(225,0,30));
        	  g.drawLine(Px, Py, Px, Py);
        	  
         
          }else if(m == 2) {           //选中C
        	  Px = (Cx+Px)/2;
        	  Py = (Cy+Py)/2;
        	  g.setColor(new Color(0,35,123));
        	  g.drawLine(Px, Py, Px, Py);
        	  
          }
        }
       
    }
    
    //将g设置为全局变量
    private Graphics g;
    
}

  运行结果：



 

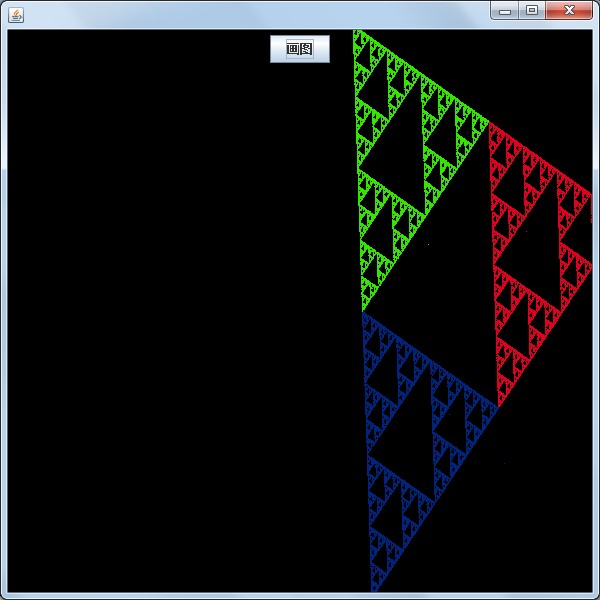
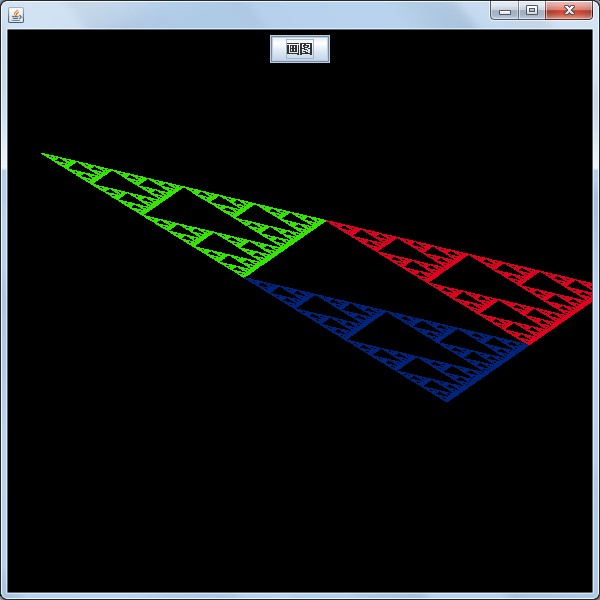
 仔细观察你会发现上面的每个图像的规律，这像上面的那一颗树枝，看上去没有什么规律，其实他的每一个小树枝都和大的树枝一模一样，不信你仔细看，这就是递归的神奇之处，把一个大的东西分成一个一个小的东西，这就是分形的精髓，我们也从中可以看出世间万物的规律，大的事务都是由小的事物组成，只要你有一双慧眼，你就会看出他们的规律。这种感觉真的很好。

 

评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值