数据结构与算法从0开始炼代码（4）

上面文章对较慢的三个排序算法进行了实现

下面开始对较好的三个排序算法进行实现（快排；堆排；归并排）

这里给出所有算法的时间复杂度

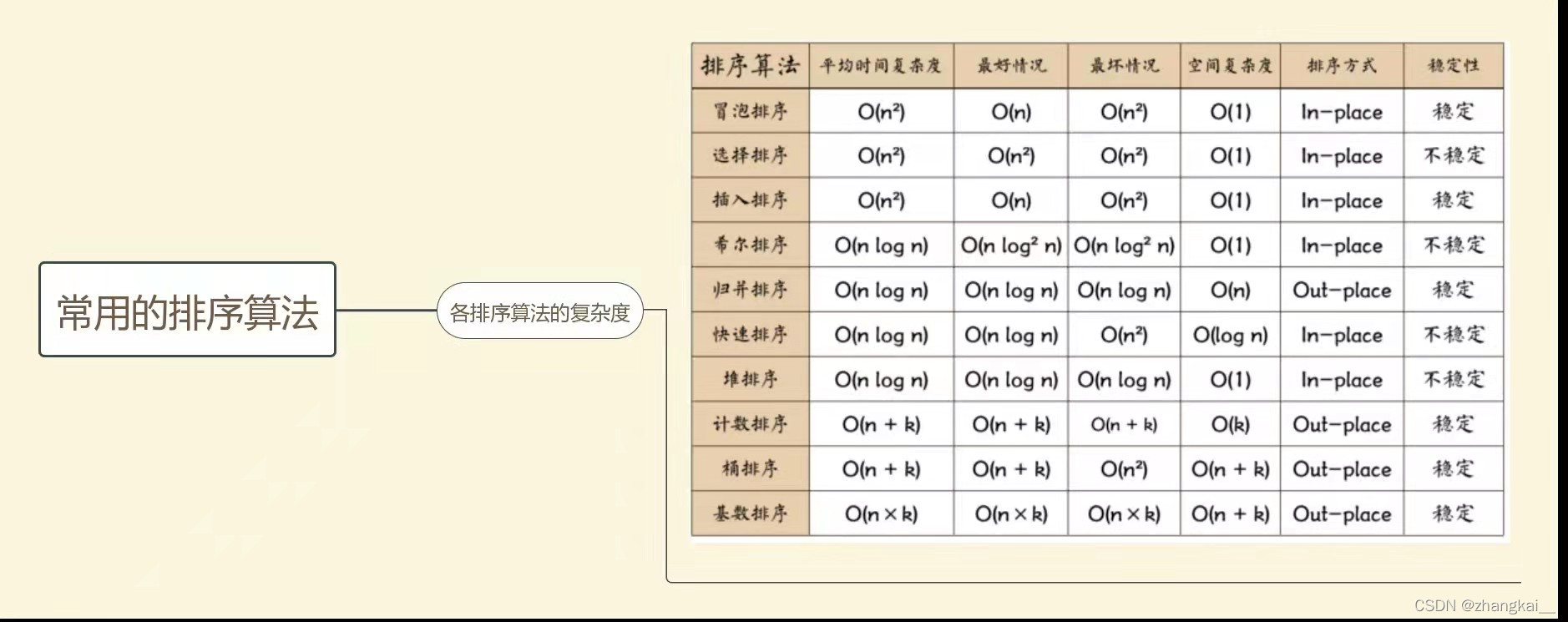
下面开始快速排序

'''_*_coding:utf-8_*_
    author:zhangkai
    time:2022
'''

import sys
import random
import copy
import time

sys.setrecursionlimit(100000) #最大递归深度，原来只有1000

def bubbling_sort(listt):
    count=1
    while count<len(listt):                      #需要排序的趟数是列表长度减-1由于趟数是只要进来就要开始一次了所以初始为1
        flag = False                             #标志位，用来标志是否进行了换位
        for i in range(0,(len(listt)-count)):    #i代表要在无序区间内进行排序搜索，无序区间为：列表长度-排序趟数，
                                                 # 每排一次说明出去一个元素，所以减去趟数就相当于减去有序数
            if listt[i]>listt[i+1]:
                listt[i],listt[i+1]=listt[i+1],listt[i]
                flag=True
        #print('listt%s; 趟数：%s'%(listt,count))
        count+=1
        if flag==False:
            break

def quick_sort(listt,left,right):                 #列表和左右指针的位置
    flagfirst = left                              #循环内部需要的头尾指针，用来标记当前传入的数组的左右指针，
                                                 # 虽然会递归，在每次递归后的新值重新赋给头尾指针
    flagend = right
    if left<right:                                #只有当存在两个及以上的数字时，才需要排序
        mid = flagend                              #先把mid放再末尾下标
        temp = listt[flagfirst]                    #将对比数拿出，存进变量，这里选取第一个为对比数，也可以是任意位置
        while flagfirst<flagend:
            if listt[flagend]<temp:                 #从右往左走，如果发现对比数右边有小于它的数
                listt[flagfirst]=listt[flagend]     #把小于数放入对比数位置，说明小于数在对比数的左侧
                flagfirst+=1                        #由于当前左指针在对比数下标位置，所以要从对比数下一个位置开始往右找比它大的数
                while flagfirst<flagend:            #只有右指针找到小于对比数的下标后，有指针位置才“空”，才能进行从左往右找
                    if listt[flagfirst]>temp:
                        listt[flagend]=listt[flagfirst]
                        break                       #如果从左指针下标找到比对比数大的数，放入右边空位，右边无空位，
                                                    # 又要从右往左找，所以左边不必循环
                    flagfirst+=1                    #一直没找到就往右移一位，直到找到或者与有指针汇合
            if flagfirst==flagend:                  #这里当左右指针汇合，说明一轮排序结束，直接退出，右指针不必再往左走
                break
            flagend-=1                              #否则右指针左移，继续找右侧小于对比数的位置下标
        if flagfirst==flagend:                      #如果左右指针汇合
            mid=flagfirst                           #mid记录位置，并把对比值放到mid位置，此时mid左边元素全比mid小，mid右边元素全比mid大
            listt[mid]=temp
        quick_sort(listt,left,mid-1)                #递归被mid分开的两端小数组，左侧
        quick_sort(listt,mid+1,right)               #右侧

listcs=[5,7,4,6,3,1,2,9,8]
li=list(range(10000))                               #测试数组
random.shuffle(li)
print(li)
li1=copy.deepcopy(li)
li2=copy.deepcopy(li)
#listcs1=[8,4,3,6,1,9,10,54,35,20]
#quick_sort(listcs,0,len(listcs)-1)
t0=time.time()
bubbling_sort(li1)
print("bubbling",time.time()-t0,li1)        #冒泡对比
ti=time.time()
quick_sort(li2,0,len(li2)-1)
print("qucik",time.time()-ti,li2)

 这里代码对于快速排序过程进行了详细注解，并且将其与冒泡排序效率进行了对比。