数据结构与算法从0开始炼代码（3）-优快云博客

本文链接：https://blog.youkuaiyun.com/zhangkai__/article/details/123820776

本文详细介绍了几种常见的排序算法，包括冒泡排序、选择排序和直接插入排序等较慢的排序方法。通过对这些算法的具体实现和代码示例进行分析，帮助读者理解它们的工作原理及效率特点。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

下面这篇文章开始对于排序问题开始代码编写

排序问题分类

较慢：冒泡排序；选择排序；直接插入排序

较好：快速排序；归并排序；堆排序

其他：希尔排序；桶排序；计数排序；基数排序

首先这篇文章是关于较慢排序的这三种排序方法，这三种方法排序一般时间复杂度都在 $O(n^{2})$ 级别，属于较差排序方式

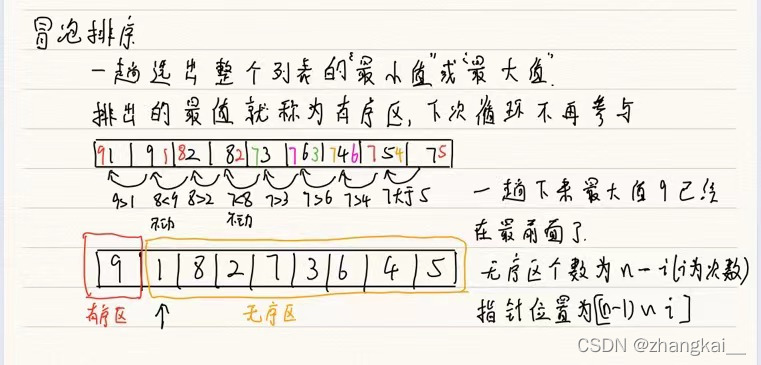
（1）冒泡排序

笔记字写得太丑，正在练字帖，如果有同学有兴趣的话，将就看一下。。

'''_*_coding:utf-8_*_
    author:zhangkai
    time:2022
'''
import random


def bubbling_sort(listt):
    count=1
    while count<len(listt):                      #需要排序的趟数是列表长度减-1由于趟数是只要进来就要开始一次了所以初始为1
        flag = False                             #标志位，用来标志是否进行了换位
        for i in range(0,(len(listt)-count)):    #i代表要在无序区间内进行排序搜索，无序区间为：列表长度-排序趟数，
                                                 # 每排一次说明出去一个元素，所以减去趟数就相当于减去有序数
            if listt[i]>listt[i+1]:
                listt[i],listt[i+1]=listt[i+1],listt[i]
                flag=True
        print('listt%s; 趟数：%s'%(listt,count))
        count+=1
        if flag==False:
            break


#listcs=[random.randint(0,20) for i in range(10)]  #测试数据
listcs1=[3,2,4,6,5,9,8,7,1]
listcs2=[9,8,7,1,2,3,4,5,6]
print('listcs',listcs2)
bubbling_sort(listcs2)

（2）选择排序

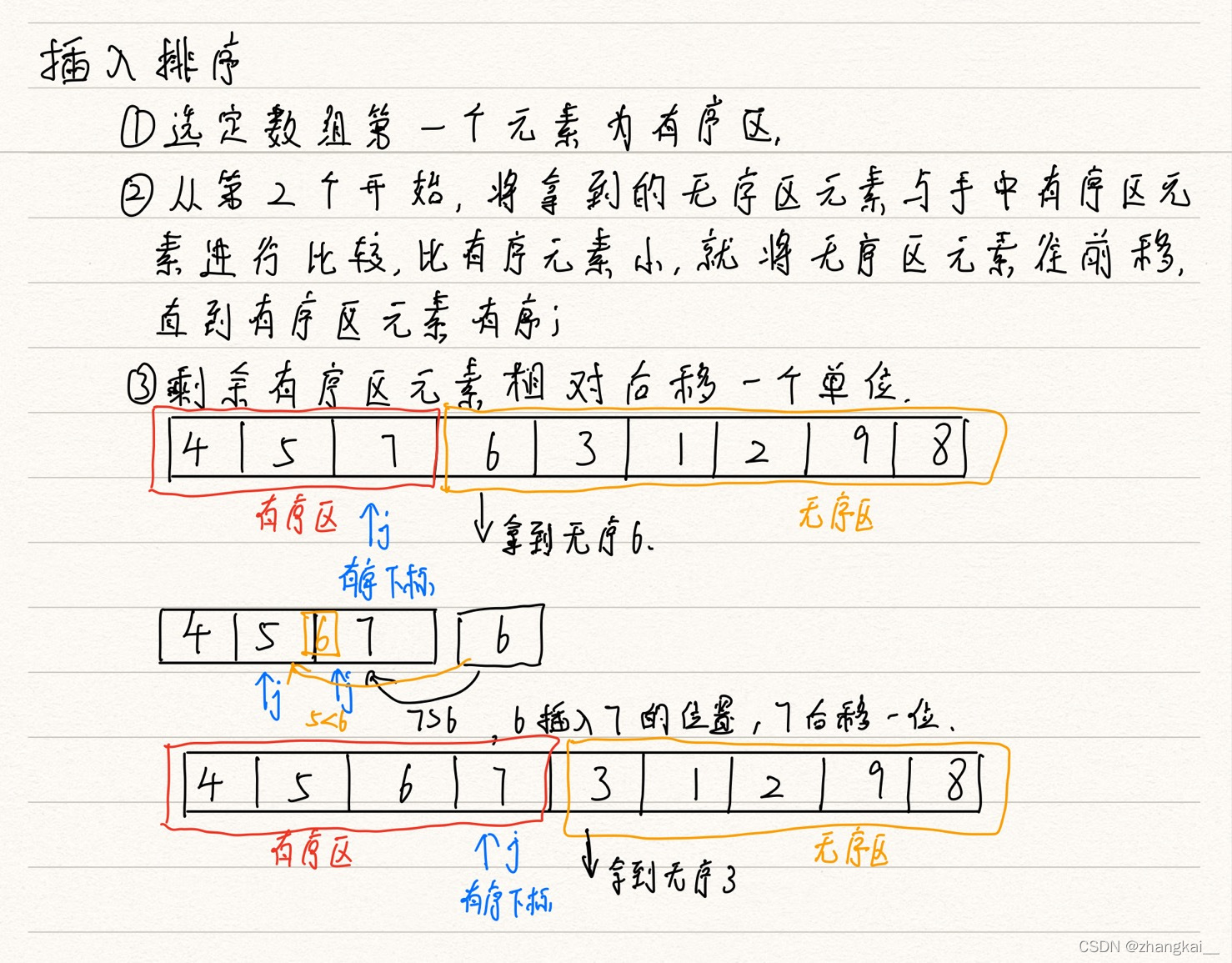
（3）直接插入排序

'''_*_coding:utf-8_*_
    author:zhangkai
    time:2022
'''
def insert_sort(listt):
    for i in range(1,len(listt)):          #无序数组池
        flag=i-1                           #flag代表有序数组最末位下标，以便新元素插入前移
        temp=listt[i]
        while flag>=0 and temp<listt[flag]: #每比较一次，flag就会前移，如果flag<0，说明新元素最小，应在最前面
            #flag-=1                         #无序数比当前有序数小，需要前插
            listt[flag+1]=listt[flag]       #找到无序数的正确位置，插入，有序组整体后移
            listt[flag]=temp
            flag -= 1                       # 无序数比当前有序数小，需要前插
        print('flag',flag,listcs)

listcs=[3,2,4,1,5,7,9,6,8]
print(listcs)
insert_sort(listcs)
print(listcs)