零点和极点到底影响了什么?什么是最小相位系统?
零点、极点、稳定、因果、最小相位是信号系统中经常听到名词,也许有的同学对这些概念有所了解,但对它们之间的关系却不甚了解,这篇文章我们就来看一下,它们之间到底有什么关系?零点和极点是怎么对系统产生应影响的?
下面我们先来看几个信号系统中的基本概念,知道了这几个概念才能继续深入下去。
1. 信号系统基本概念
1.1 静态系统和动态系统
如果一个离散系统在任意时刻n的输出至多依赖于同一时刻的输入样本,而与过去或者将来的输入样本无关,那么该系统就称为静态的,或者无记忆的。对于其他情况,则该系统称为动态的或者有记忆的。
如果系统在时刻n的输出完全由区间n-N到n内的输入样本确定,那么称该系统具有持续时间为N的记忆。如果N=0,那么系统是静态的。如果0<N<∞,那么称系统是有记忆的。但是,如果N=∞,那么系统称为无限记忆的。
1.2 时不变系统和时变系统
如果一个系统的输入-输出特性不随时间变化,那么该系统称为时不变系统。即如果y(n) = F(x(n)),且y(n-k) = F(x(n-k)),那么该系统就叫时不变系统。
1.3线性系统和非线性系统
这个理解起来就比较直观了,一个系统是线性的,当且仅当对任意输入序列x1(n)和x2(n),以及任意常数a1和a2,有如下公式:
F[a1x1(n)+a2x2(n)]=a1F[x1(n)]+a2F[x2(n)]
F[a_1 x_1(n) + a_2 x_2(n)] = a_1 F[x_1(n)] + a_2 F[x_2(n)]
F[a1x1(n)+a2x2(n)]=a1F[x1(n)]+a2F[x2(n)]
1.4因果系统和非因果系统
如果一个系统在任意时刻n的输出仅依赖于当前和过去的输入,而与将来的输入无关,那么这个系统就称为是因果的。即:
y(n)=F[x(n),x(n−1),x(n−2),...]
y(n) = F[x(n), x(n-1), x(n-2),...]
y(n)=F[x(n),x(n−1),x(n−2),...]
如果一个系统不满足这个定义,那么就称它为非因果的。这样系统的输出不但依赖于当前和过去的输入,而且还依赖于将来的输入。
在实际的信号处理应用中,我们无法观察到信号将来的值,因此,非因果系统在物理上是不可实现的。但如果是脱机处理,就有可能实现非因果系统,这是因为信号的所有值在处理过程中都是可用的,这在图像处理和离线的雷达信号处理中都很常见。
对于因果线性时不变系统,单位采样响应h(n)必须满足:
h(n)=0,n<0
h(n) = 0, n<0
h(n)=0,n<0
1.5稳定系统和不稳定系统
稳定是系统的一个重要属性,在实际应用中必须要考虑。不稳定的系统常常显示出不规律的、极端的特性,并且在实际执行时会产生溢出。因此定义一个任意的弛豫系统称为有界输入-有界输出稳定,当且仅当每个有界输入产生有界的输出。
对于线性时不变系统,其稳定的充分必要条件是:
∑n=−∞∞∣h(n)∣<∞
\sum_{n=-\infty}^{\infty} |h(n)| < \infty
n=−∞∑∞∣h(n)∣<∞
2 零点和极点
零点是指使z变换X(z)的值为零的z值,极点是指使X(z)的值为∞的z值。如果X(z)是有理分式,表示为:
X(z)=B(z)A(z)=b0+b1z−1+⋯+bMz−Ma0+a1z−1+⋯+aNz−N=∑k=0Mbkz−k∑k=0Nakz−k
X(z)=\frac{B(z)}{A(z)}=\frac{b_{0}+b_{1} z^{-1}+\cdots+b_{M} z^{-M}}{a_{0}+a_{1} z^{-1}+\cdots+a_{N} z^{-N}}=\frac{\sum_{k=0}^{M} b_{k} z^{-k}}{\sum_{k=0}^{N} a_{k} z^{-k}}
X(z)=A(z)B(z)=a0+a1z−1+⋯+aNz−Nb0+b1z−1+⋯+bMz−M=∑k=0Nakz−k∑k=0Mbkz−k
如果a0≠0,b0≠0,那么可以将分式写成如下形式:
X(z)=B(z)A(z)=b0a0z−M+N(z−z1)(z−z2)⋯(z−zM)(z−p1)(z−p2)⋯(z−pN)X(z)=GzN−M∏k=1M(z−zk)N(z−pk)
\begin{array}{l}
X(z)=\frac{B(z)}{A(z)}=\frac{b_{0}}{a_{0}} z^{-M+N} \frac{\left(z-z_{1}\right)\left(z-z_{2}\right) \cdots\left(z-z_{M}\right)}{\left(z-p_{1}\right)\left(z-p_{2}\right) \cdots\left(z-p_{N}\right)} \\
X(z)=G z^{N-M} \frac{\prod_{k=1}^{M}\left(z-z_{k}\right)}{N}\left(z-p_{k}\right)
\end{array}
X(z)=A(z)B(z)=a0b0z−M+N(z−p1)(z−p2)⋯(z−pN)(z−z1)(z−z2)⋯(z−zM)X(z)=GzN−MN∏k=1M(z−zk)(z−pk)
因此,X(z)在z=z1,z2,…,zM处有M个有限零点;在z=p1,p2,…,pN处有N个有限极点;在原点z=0处有|N-M|个零点(N>M)或极点(N<M)
2.1 收敛域和因果系统的关系
z变换大家肯定都知道,但也许有些同学会忘记,在z变换的定义中,除了表达式外,还要指定收敛域。z变换的定义为:
X(z)=∑n=−∞∞x(n)z−n
X(z) = \sum_{n=-\infty}^{\infty} x(n) z^{-n}
X(z)=n=−∞∑∞x(n)z−n
收敛域是使X(z)的值为有限的所有z值的集合,所以收敛域肯定不包含极点,是极点之外的地方。
这里有一个重要结论:因果信号的收敛域是某个半径r的圆的外部;非因果信号的收敛域是某个半径r的内部。
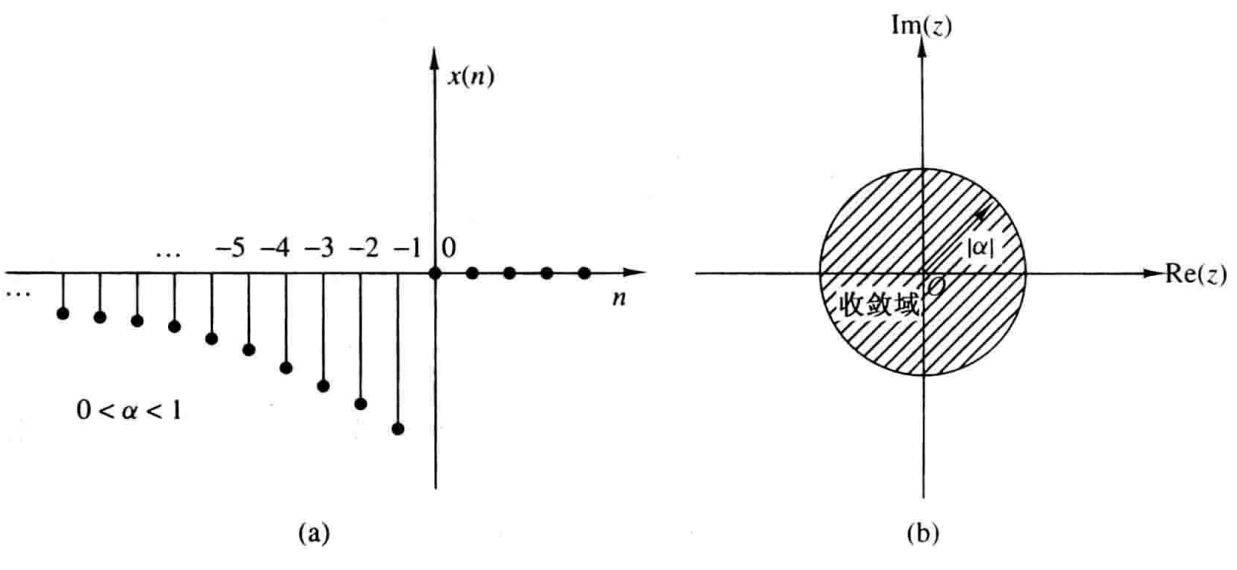
下面举两个例子来说明该结论,首先来看因果信号:
x(n)=αnu(n)={αn,n⩾00,n<0
x(n)=\alpha^{n} u(n)=\left\{\begin{array}{ll}
\alpha^{n}, & n \geqslant 0 \\
0, & n<0
\end{array}\right.
x(n)=αnu(n)={αn,0,n⩾0n<0
该信号的z变换为:
X(z)=∑n=0∞αnz−n=∑n=0∞(αz−1)n
X(z)=\sum_{n=0}^{\infty} \alpha^{n} z^{-n}=\sum_{n=0}^{\infty}\left(\alpha z^{-1}\right)^{n}
X(z)=n=0∑∞αnz−n=n=0∑∞(αz−1)n
如果∣αz−1∣<1|\alpha z^{-1}|<1∣αz−1∣<1或者等价的∣z∣>∣α∣|z|>|\alpha|∣z∣>∣α∣,那么这个幂级数收敛于1/(1−αz−1)1/(1-\alpha z^{-1})1/(1−αz−1),从而得到:
x(n)=αnu(n)⟷zX(z)=11−αz−1, 收收敛域: ∣z∣>∣α∣
x(n)=\alpha^{n} u(n) \stackrel{z}{\longleftrightarrow} X(z)=\frac{1}{1-\alpha z^{-1}}, \quad \text { 收收敛域: }|z|>|\alpha|
x(n)=αnu(n)⟷zX(z)=1−αz−11, 收收敛域: ∣z∣>∣α∣
这里极点就是z=∣α∣z=|\alpha|z=∣α∣,收敛域为半径为∣α∣|\alpha|∣α∣的圆的外部,下图(a)表示信号x(n)的时域波形,(b)表示其收敛域。

对于非因果信号
x(n)=−αnu(−n−1)={0,n⩾0−αn,n⩽−1
x(n)=-\alpha^{n} u(-n-1)=\left\{\begin{array}{ll}
0, & n \geqslant 0 \\
-\alpha^{n}, & n \leqslant-1
\end{array}\right.
x(n)=−αnu(−n−1)={0,−αn,n⩾0n⩽−1
其z变换为:
x(n)=−αnu(−n−1)⟷zX(z)=−11−αz−1, 收敘域: ∣z∣<∣α∣
x(n)=-\alpha^{n} u(-n-1) \stackrel{z}{\longleftrightarrow} X(z)=-\frac{1}{1-\alpha z^{-1}}, \quad \text { 收敘域: }|z|<|\alpha|
x(n)=−αnu(−n−1)⟷zX(z)=−1−αz−11, 收敘域: ∣z∣<∣α∣
这里极点也是z=∣α∣z=|\alpha|z=∣α∣,为收敛域是半径为∣α∣|\alpha|∣α∣的圆的内部。
对于双边信号x(n)=αnu(n)+bnu(−n−1)x(n) = \alpha^{n} u(n) + b^{n} u(-n-1)x(n)=αnu(n)+bnu(−n−1),可以将该信号分为两部分:第一部分是因果信号,第二部门是非因果信号。其z变换要分两种情况讨论:
- 当∣b∣<∣α∣|b| < | \alpha|∣b∣<∣α∣时,两个信号的收敛域没有重叠部分,因此此时X(z)不存在,如下图(a)所示
- 当∣b∣>∣α∣|b| > | \alpha|∣b∣>∣α∣时,两个信号的收敛域的重叠部分是一个环状区域,此时的收敛域为∣α∣<∣z∣<∣b∣|\alpha| < |z| < |b|∣α∣<∣z∣<∣b∣,如下图(b)所示

2.2 收敛域和稳定系统的关系
我们前面讲过,线性时不变系统稳定的充分必要条件就是:
∑n=−∞∞∣h(n)∣<∞
\sum_{n=-\infty}^{\infty} |h(n)| < \infty
n=−∞∑∞∣h(n)∣<∞
其z变换为
H(z)=∑n=−∞∞h(n)z−n
H(z) =\sum_{n=-\infty}^{\infty} h(n)z^{-n}
H(z)=n=−∞∑∞h(n)z−n
那么
∣H(z)∣⩽∑n=−∞∞∣h(n)z−n∣=∑n=−∞∞∣h(n)∣∣z−n∣
|H(z)| \leqslant \sum_{n=-\infty}^{\infty} |h(n)z^{-n}|=\sum_{n=-\infty}^{\infty} |h(n)||z^{-n}|
∣H(z)∣⩽n=−∞∑∞∣h(n)z−n∣=n=−∞∑∞∣h(n)∣∣z−n∣
当在单位圆上计算时(即|z|=1),得
∣H(z)∣⩽∑n=−∞∞∣h(n)∣
|H(z)| \leqslant \sum_{n=-\infty}^{\infty}|h(n)|
∣H(z)∣⩽n=−∞∑∞∣h(n)∣
因此,如果线性是不变系统是稳定的,那么单位圆包含于H(z)的收敛域内。
由上一节可知,因果系统的收敛域是在某个半径为r的圆外面,因此对于线性时不变因果稳定系统,其收敛域为
r<∣z∣<1
r < |z| < 1
r<∣z∣<1
又由于收敛域中不包含极点,因此线性时不变因果稳定系统的极点都在单位圆内。这里再补充一点,单位圆上的z变换就是傅里叶变换。
我们还是以上一节中的x(n)=anu(n)x(n)=a^{n}u(n)x(n)=anu(n)为例,我们知道,它的收敛域是∣z∣>∣a∣|z|>|a|∣z∣>∣a∣,在p1=ap_1=ap1=a处有一个单极点。下图说明了与单位圆相关的极点位置的信号行为特性。
- 如果极点位于单位圆内,则信号是衰减的;
- 如果极点位于单位圆上,则先后是恒定的;
- 如果极点位于单位圆外,则信号是增长的;

但如果是一个多重极点,则情况会有所不同。我们以一个双重极点的信号为例
x(n)=nanu(n)
x(n) = na^{n}u(n)
x(n)=nanu(n)
其z变换为
X(z)=az−1(1−az−1)2
X(z) = \frac{az^{-1} }{(1-az^{-1})^{2}}
X(z)=(1−az−1)2az−1
此时,位于单位圆上的实的双重极点,其结果是无界的信号,因此,如果单位圆上有多重极点,我们就需要非常小心。

2.3 零极点和频率响应的关系
说到零极点和频率响应的关系,就必须提一下z变换的z域和拉普拉斯变换的s域的关系,因为看频响的话,都是转换到s域来看。s平面的左半平面映射到z平面的单位圆内;s平面的右半平面映射到单位圆外部;s平面的jw轴映射到z平面的单位圆。因此,线性时不变因果稳定的系统,其极点都在s平面的左半平面。
当系统稳定时,有
H(ω)=H(s)∣s=jω=K∏r=1m(jω−zr)∏k=1n(jω−pk)
H(\omega)=\left.H(s)\right|_{s=j \omega}=K \frac{\prod_{r=1}^{m}\left(j \omega-z_{r}\right)}{\prod_{k=1}^{n}\left(j \omega-p_{k}\right)}
H(ω)=H(s)∣s=jω=K∏k=1n(jω−pk)∏r=1m(jω−zr)
其中,zrz_rzr为系统的零点,pkp_kpk为系统的极点。
那么系统的幅频特性为
∣H(ω)∣=∣K∣∏r=1m∣jω−zr∣∏k=1n∣jω−pk∣
|H(\omega)|=|K| \frac{\prod_{r=1}^{m}\left|j \omega-z_{r}\right|}{\prod_{k=1}^{n}\left|j \omega-p_{k}\right|}
∣H(ω)∣=∣K∣∏k=1n∣jω−pk∣∏r=1m∣jω−zr∣
相频特性为
φ(ω)=∑r=1marg(jω−zr)−∑k=1narg(jω−pk)
\varphi(\omega)=\sum_{r=1}^{m} \arg \left(j \omega-z_{r}\right)-\sum_{k=1}^{n} \arg \left(j \omega-p_{k}\right)
φ(ω)=r=1∑marg(jω−zr)−k=1∑narg(jω−pk)
定义零点矢量为从零点指向jwjwjw的有向线段:N=jw−zr=NrejarN=jw-z_r = N_r e^{ja_r}N=jw−zr=Nrejar
定义极点矢量为从极点指向jwjwjw的有向线段:M=jw−pk=MkejβkM = jw - p_k = M_k e^{j\beta_k}M=jw−pk=Mkejβk
那么,有
H(ω)=K∏r=1m(jω−zr)∏k=1n(jω−pk)=K∏r=1mNrejαr∏k=1nMkejβk
H(\omega)=K \frac{\prod_{r=1}^{m}\left(j \omega-z_{r}\right)}{\prod_{k=1}^{n}\left(j \omega-p_{k}\right)}=K \frac{\prod_{r=1}^{m} N_{r} e^{j \alpha_{r}}}{\prod_{k=1}^{n} M_{k} e^{j \beta_{k}}}
H(ω)=K∏k=1n(jω−pk)∏r=1m(jω−zr)=K∏k=1nMkejβk∏r=1mNrejαr
所以系统的幅频特性为
∣H(ω)∣=∣K∣∏r=1mNr∏k=1nMk
|H(\omega)|=|K| \frac{\prod_{r=1}^{m} N_{r}}{\prod_{k=1}^{n} M_{k}}
∣H(ω)∣=∣K∣∏k=1nMk∏r=1mNr
相频特性为
φ(w)=∑r=1mar−∑k=1nβk
\varphi (w) = \sum_{r=1}^{m}a_r - \sum_{k=1}^{n} \beta_k
φ(w)=r=1∑mar−k=1∑nβk
也就说,**系统的幅频特性就是系统的零点矢量模的乘积与极点矢量模的乘积之比,相频特性是零点矢量相角的和与极点矢量相角的和之差。**随着频率w从0到∞增大,零点矢量和极点矢量均在变化。

下面举一个例子,已知系统函数为
H(s)=s(s+a1)(s+a2)
H(s) = \frac{s}{(s+a_1)(s+a_2)}
H(s)=(s+a1)(s+a2)s
我们来根据它的零极点,粗略的画一下幅频特性和相频特性。
由表达式可知,系统零点在s=0s=0s=0处,极点在s=−a1s=-a_1s=−a1和s=−a2s=-a_2s=−a2处。

零点矢量的相角一直为ψ1=90o\psi_1 =90^{o}ψ1=90o,模值为N1=∣w∣N_1=|w|N1=∣w∣;模值从0增大到无穷大。
极点矢量的相角θ1\theta_1θ1和θ2\theta_2θ2随着w的增加而增大,当w从0增大到∞时,这两个相角从0增大到90°;模值分别从∣a1∣|a_1|∣a1∣和∣a2∣|a_2|∣a2∣增大到无穷大。
因此,可以得出下面的表格。

在w为0和∞时,幅频特性都为0,在中间的某一个点处,幅频特性会达到峰值;而相角差则从开始的90°一直减到-90°。因此幅频特性和相频特性分别如下:

至于为什么在幅频特性达到峰值时,相频特性刚好为0,这也是可以严格证明的。我们这里就不再证明了,因为我们只是为了粗略画出这两个特性。
对于零极点和频响的关系,有如下几个特性:
- 若在原点jw=0jw=0jw=0处有零点,则∣H(0)=0∣|H(0)=0|∣H(0)=0∣,否则∣H(w)∣|H(w)|∣H(w)∣从某一非0数值开始;
- 若系统函数的某一个极点(假设p1=−a+jβp_1=-a+j\betap1=−a+jβ)十分靠近虚轴(若换成z平面,则是如果某一极点十分靠近单位圆),也就是说aaa的值非常小,则当www在该极点虚部附近处,幅频响应有一峰值,相频响应急剧减小;

- 如果系统函数有一零点(假设z1=−a+jβz_1=-a+j\betaz1=−a+jβ)十分靠近虚轴(若换成z平面,则是如果某一零点十分靠近单位圆),则当www在该零点虚部附近处,幅频响应有一谷值,相频响应急剧增大;
- 在jw=∞jw=\inftyjw=∞处的大小主要看零点极点的个数,如果零点比极点多,则∣H(w)∣→∞|H(w)|\rightarrow \infty∣H(w)∣→∞;若极点比零点多,则∣H(w)∣→0|H(w)|\rightarrow 0∣H(w)∣→0;若零点和极点一样多,则∣H(∞)∣|H(\infty)|∣H(∞)∣为某一有限值。
3 最小相位系统
对于FIR系统(没有极点),如果系统函数的所有零点都位于单位圆内,则称该系统为最小相位系统;如果系统函数的所有零点都位于单位圆外,则称该系统为最大相位系统;如果一部分零点位于单位圆内,一部分零点位于单位圆外,则称该系统为混合相位系统或非最小相位系统。
对于IIR系统(存在极点),如果系统函数的所有零点和极点都在单位圆内,则称该系统为最小相位系统。
3.1 为什么叫最小相位系统
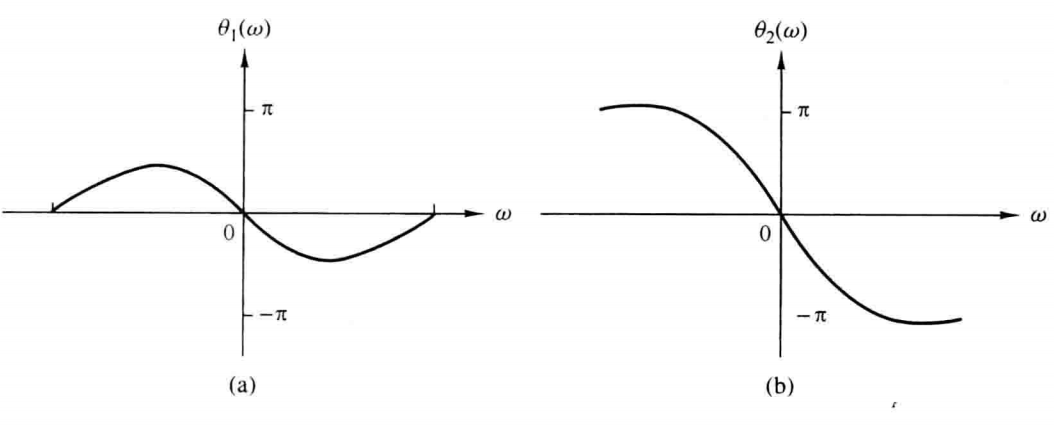
因此其相频特性φ(w)\varphi (w)φ(w)在w=0w=0w=0和w=πw=\piw=π之间经历的净相位变化为零;就像下图(a)所示;而下图(b)中,在w=0w=0w=0和w=πw=\piw=π之间的净相位变化是π\piπ,因此称为最大相位系统。
3.2 最小相位系统有特点
最小相位系统的特性很多,主要的特性为:
- 最小相位系统是因果且稳定的;
- 其逆系统也是因果且稳定的;
- 在所有具有相同幅频响应的零-极点系统中,最小相位系统的群时延最小。
欢迎关注微信公众号:Quant_Times






















 2万+
2万+










