【递推关系】HDU-1143 Tri Tiling_hdu 递推-优快云博客

本文链接：https://blog.youkuaiyun.com/zhanggirlzhangboy/article/details/103568139

本文详细解析了一种特定的递推关系F(n)=4*F(n-2)-F(n-4)的推导过程，通过分解F(n)为两种情况，并结合动态规划的思想，给出了高效的代码实现，用于计算特定序列的值。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

在这里插入图片描述

注解

1、递推关系的应用。
2、参考https://www.cnblogs.com/KirinSB/p/9409131.html这里的图
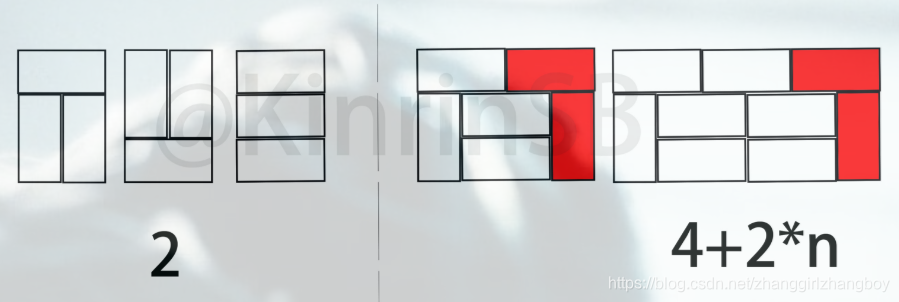
在这里插入图片描述
3、F(n)由两种情况组成，
第一种：F(n) = 3 * F(n-2)，也就是图中左边的情况
第二种：F(n) = 2 * F(n-4) + 2 * F(n-6) + … + 2 * F(0)，也就是图中右边的情况，2不是基本单元，4、6、8。。。才是基本单元。
4、综合上面两种情况和两个表达式，将其相加，得到
F(n) = 3 * F(n-2) + 2 * F(n-4) + 2 * F(n-6) + … + 2 * F(0)，(式1）
同样的，F(n-2) = 3 * F(n-4) + 2 * F(n-6) + 2 * F(n-8) + … + 2 * F(0)，（式2）
将(式2)移项，得到F(n-2) - F(n-4) = 2 * F(n-4) + 2 * F(n-6) + … + 2 * F(0)，
代入(式1)，得到最终的递推关系：F(n)=4*F(n-2)-F(n-4)。
5、以上推导都是针对偶数项，而奇数项的答案全部是0。

代码

#include <iostream>
#include <cstring>

using namespace std;

int dp[31];

void init() {
    dp[0] = 1;
    dp[2] = 3;
    for(int i=4; i<=30; i+=2) {
        dp[i] = 4*dp[i-2] - dp[i-4];
    }
}

int main() {

    memset(dp, 0, sizeof(dp));
    init();
    
    int n;
    cin>>n;
    while(n!=-1) {
        cout<<dp[n]<<endl;
        cin>>n;
    }

    return 0;
}

结果

在这里插入图片描述