题目描述
样例
input:
1 2 1 2 8 4
output:
2048
input:
1 2 3 4 120 180
output:
235140177
题目大意
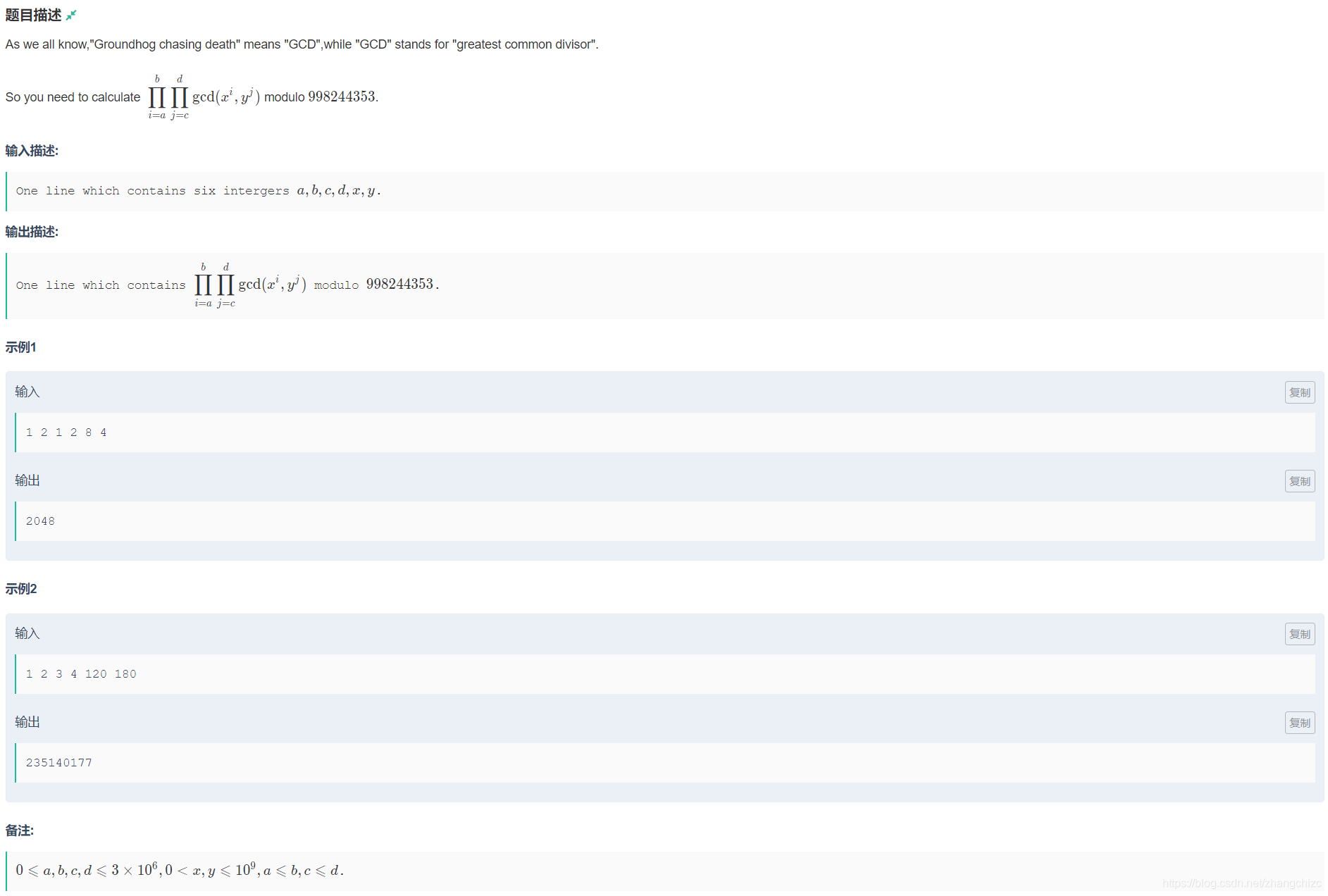
给定 a , b , c , d , x , y a,b,c,d,x,y a,b,c,d,x,y,求:
∏ i = a b ∏ j = c d gcd ( x i , y j ) \mathop{\prod}\limits_{i=a}^{b}\mathop{\prod}\limits_{j=c}^{d}\gcd(x^i,y^j) i=a∏bj=c∏dgcd(xi,yj)
分析
首先我们考虑对于 gcd ( x , y ) \gcd(x,y) gcd(x,y)的值是多少。嗯,是它们质因数分解之后的公共部分。那么对于一个数的幂次之后,其质因子的变化是乘上了这个指数。所以,看到数据范围是不可能暴力的,要从这一方面入手。
那么数据范围是允许 O ( n log n ) O(n\log n) O(nlogn)的,所以可以分解质因数,然后对于每个质因数都单独考虑,由于对别的质因数都没有干扰,所以可以放心地去搞这个。
假设我们分解:
x = p 1 a 1 ∗ p 2 a 2 … p n a n x=p_1^{a_1}*p_2^{a_2}\dots p_n^{a_n} x=p1a1∗p2a
 质因数分解与费马小定理在模拟题中的应用
质因数分解与费马小定理在模拟题中的应用





 博客介绍了如何利用质因数分解和费马小定理解决Groundhog Chasing Death问题。通过分析数据范围,提出固定其中一个变量优化算法,避免超时。讲解了在处理指数可能超过long long时使用费马小定理进行模指数运算的方法,并提供了代码实现。
博客介绍了如何利用质因数分解和费马小定理解决Groundhog Chasing Death问题。通过分析数据范围,提出固定其中一个变量优化算法,避免超时。讲解了在处理指数可能超过long long时使用费马小定理进行模指数运算的方法,并提供了代码实现。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 270
270

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








