The following problem is well-known: given integers n and m, calculate
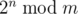 ,
,
where 2n = 2·2·...·2 (n factors), and  denotes the remainder of division of x by y.
denotes the remainder of division of x by y.
You are asked to solve the "reverse" problem. Given integers n and m, calculate
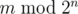 .
.
The first line contains a single integer n (1 ≤ n ≤ 108).
The second line contains a single integer m (1 ≤ m ≤ 108).
Output a single integer — the value of 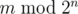 .
.
4 42
10
1 58
0
98765432 23456789
23456789
In the first example, the remainder of division of 42 by 24 = 16 is equal to 10.
In the second example, 58 is divisible by 21 = 2 without remainder, and the answer is 0.
很久没刷题了,我个人还是很喜欢codeforces的,水题
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int inf = 0x3f3f3f3f;
int main()
{
ll n,m;
cin>>n>>m;
ll now=2;
int i;
for(i=1;i<n;i++)
{
now*=2;
if(now>m)
break;
}
if(i<n)
cout<<m<<endl;
else
cout<<m%now<<endl;
return 0;
}





 给定整数n和m,求解2^n除以m的余数的逆问题。输入包含n和m,输出2的n次方除以m的商的余数。题目提供两个示例解释了计算过程。
给定整数n和m,求解2^n除以m的余数的逆问题。输入包含n和m,输出2的n次方除以m的商的余数。题目提供两个示例解释了计算过程。
















 2854
2854

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








