codeforces 913 A Modular Exponentiation

最新推荐文章于 2023-01-10 12:07:14 发布

原创最新推荐文章于 2023-01-10 12:07:14 发布 · 334 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#codeforces

acm 专栏收录该内容

57 篇文章

订阅专栏

本文介绍了一种针对特定情况下的模运算快速求解方法，通过判断2的幂次是否超过给定数值来简化计算过程。

Description
The following problem is well-known: given integers n and m, calculate

where

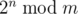
2n = 2⋅2⋅...⋅2 $2^n = 2·2·...·2$ (n factors), and denotes the remainder of division of x by y.

You are asked to solve the “reverse” problem. Given integers n and m, calculate

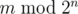
Input

The first line contains a single integer n (1 ≤ n ≤ 10 $^8$ ).

The second line contains a single integer m (1 ≤ m ≤ 10 $^8$ ).
Output

Output a single integer — the value of 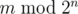m mod 2^n .
Examples

Input
4 42
Output
10

Input
1 58
Output
0

Input
98765432 23456789
Output
23456789

Note

In the first example, the remainder of division of 42 by 2 $^4$ = 16 is equal to 10.

In the second example, 58 is divisible by 2 $^1$ = 2 without remainder, and the answer is 0.

题意：输入n，m求m mod 2 $^n$
思路：因为m最大只有10 $^8$ ，所以对于很大的n大可不必将2 $^n$ 计算出来，只用判断一下是否比m大就行了。

#include <stdio.h>

int main() {
    int n, m;
    //m mod 2^n
    scanf("%d %d", &n, &m);
    int n2 = 1;
    for (int i = 0; i < n; ++i) {//做n次2的幂运算
        if (n2 * 2 <= m)n2=n2 * 2;
        else { n2 = n2 * 2; break; }//当n2大于m时中断计算
    }
    printf("%d", m%n2);
}