The following problem is well-known: given integers n and m, calculate
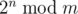 ,
,where 2n = 2·2·...·2 (n factors), and  denotes the remainder of division of x by y.
denotes the remainder of division of x by y.
You are asked to solve the "reverse" problem. Given integers n and m, calculate
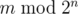 .
.The first line contains a single integer n (1 ≤ n ≤ 108).
The second line contains a single integer m (1 ≤ m ≤ 108).
Output a single integer — the value of 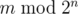 .
.
4 42
10
1 58
0
98765432 23456789
23456789
In the first example, the remainder of division of 42 by 24 = 16 is equal to 10.
In the second example, 58 is divisible by 21 = 2 without remainder, and the answer is 0.
虽然n很大,但我们发现当n>26时2^26已经超过了数据范围。所以只要输出m就行了,当n<=26时直接判断。
Code:
#include<bits/stdc++.h>
using namespace std;
int mod,k;
int power(int p,int k)
{
int ans=1,t=1;
while(k)
{
if(t==1)t=p;else t=t*t;
if(k%2==1)ans=ans*t;
k>>=1;
}
return ans;
}
int main()
{
scanf("%d%d",&k,&mod);
if(k>26)printf("%d",mod);else
printf("%d",mod%power(2,k));
return 0;
}




 本文探讨了模幂运算的“逆”问题,即给定整数n和m,求解特定条件下的模运算结果。文章提供了一种高效算法,并通过实例解释了计算过程。
本文探讨了模幂运算的“逆”问题,即给定整数n和m,求解特定条件下的模运算结果。文章提供了一种高效算法,并通过实例解释了计算过程。

















 7786
7786

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










