Machine Learning - Coursera 吴恩达机器学习教程 Week7 学习笔记（Support Vector Machines）

支持向量机SVM

在线性可分的情况下，训练数据集的样本点中与分离超平面距离最近的数据点称为支持向量(support vector)。

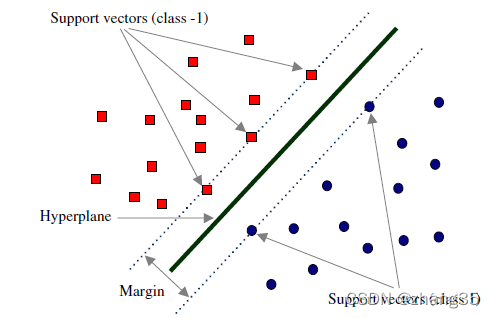
代价函数和逻辑回归比较相似：

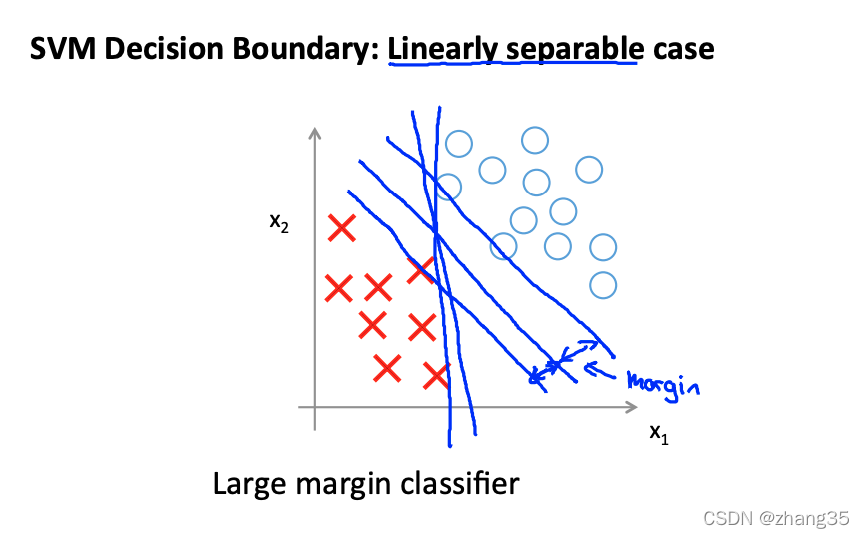
又称为大间隔分类器，能找到最佳的线性分类位置：

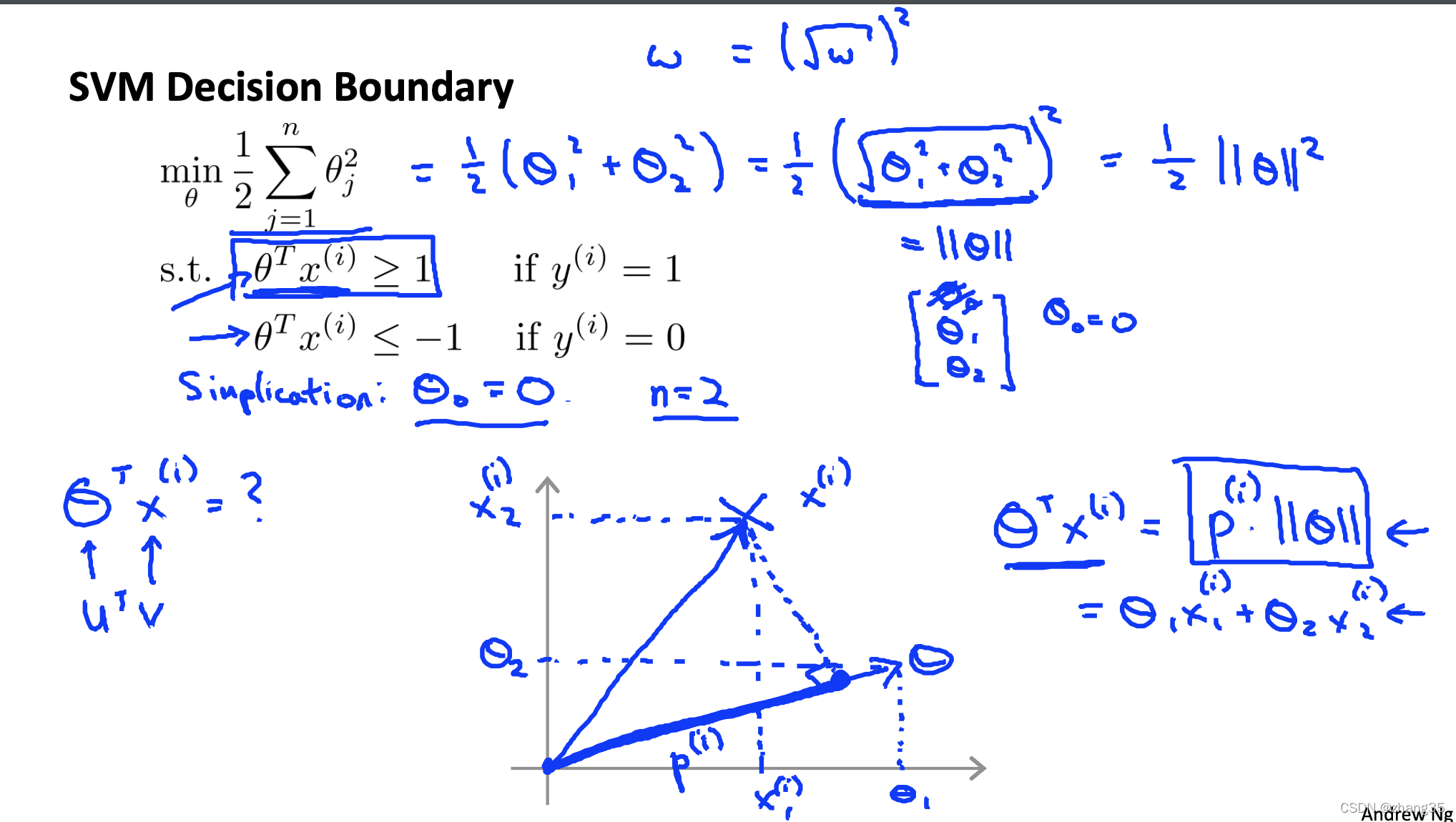
向量内积的物理意义，相当于一个向量在另一个上面的投影长度的乘积：

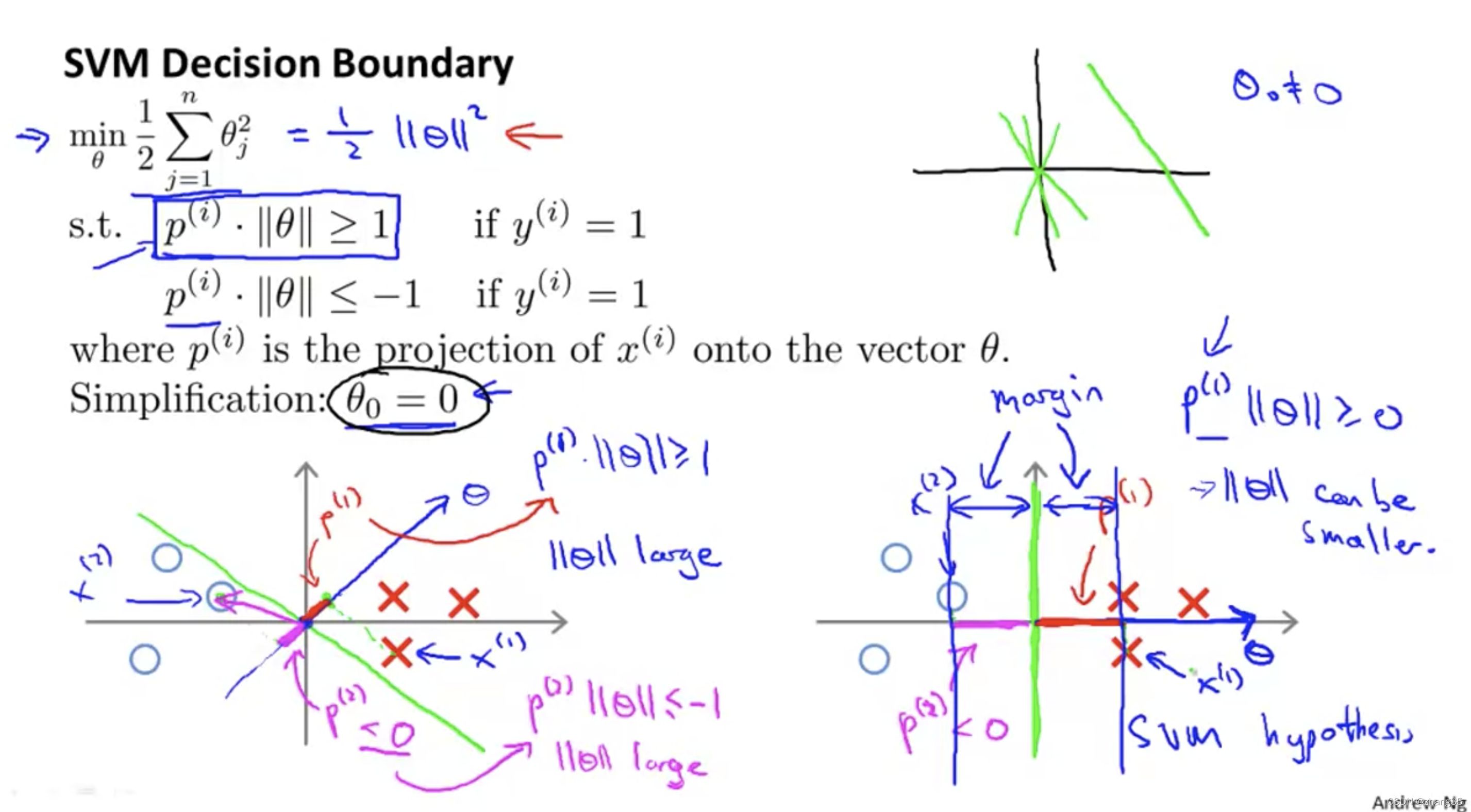
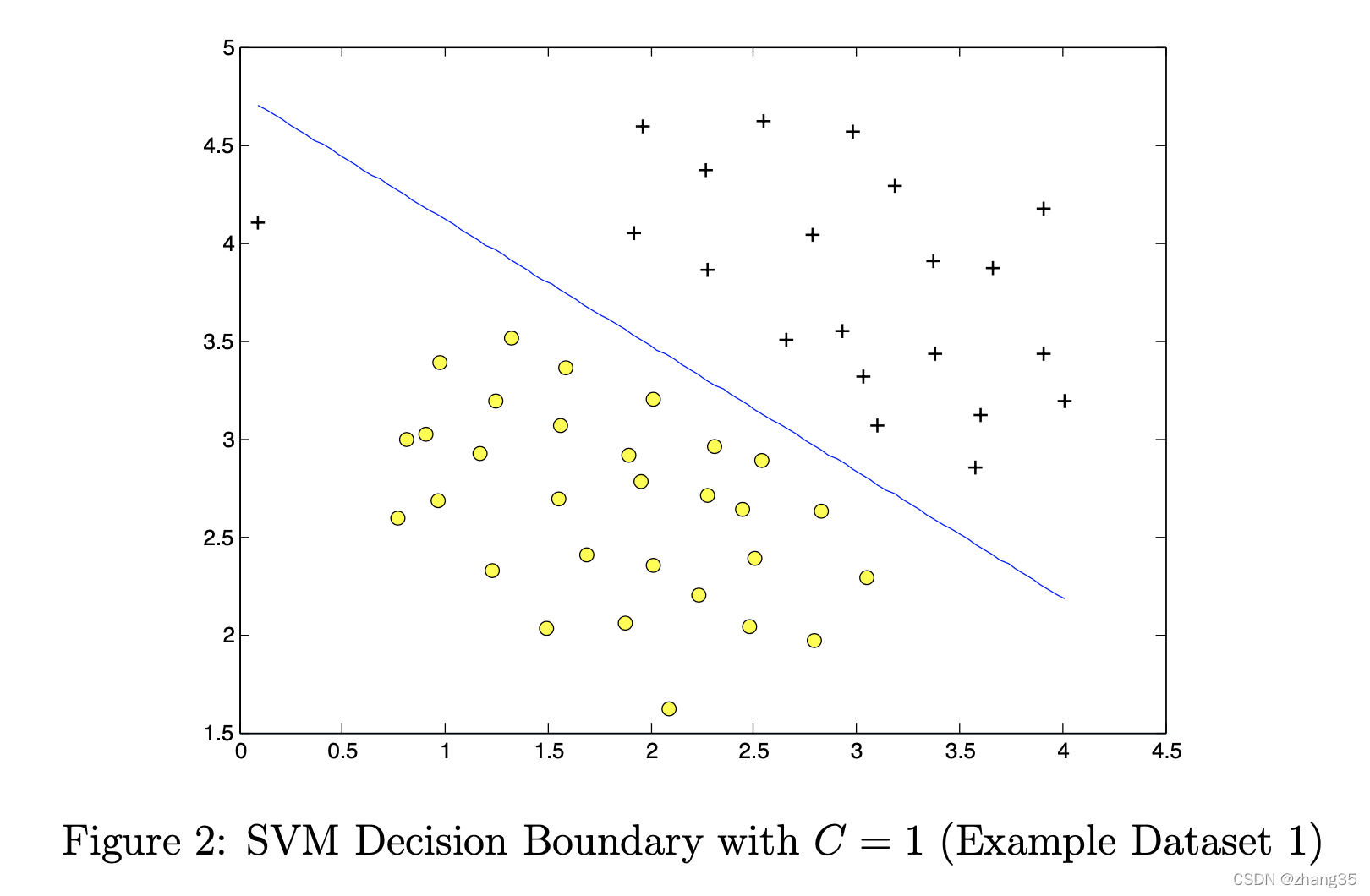
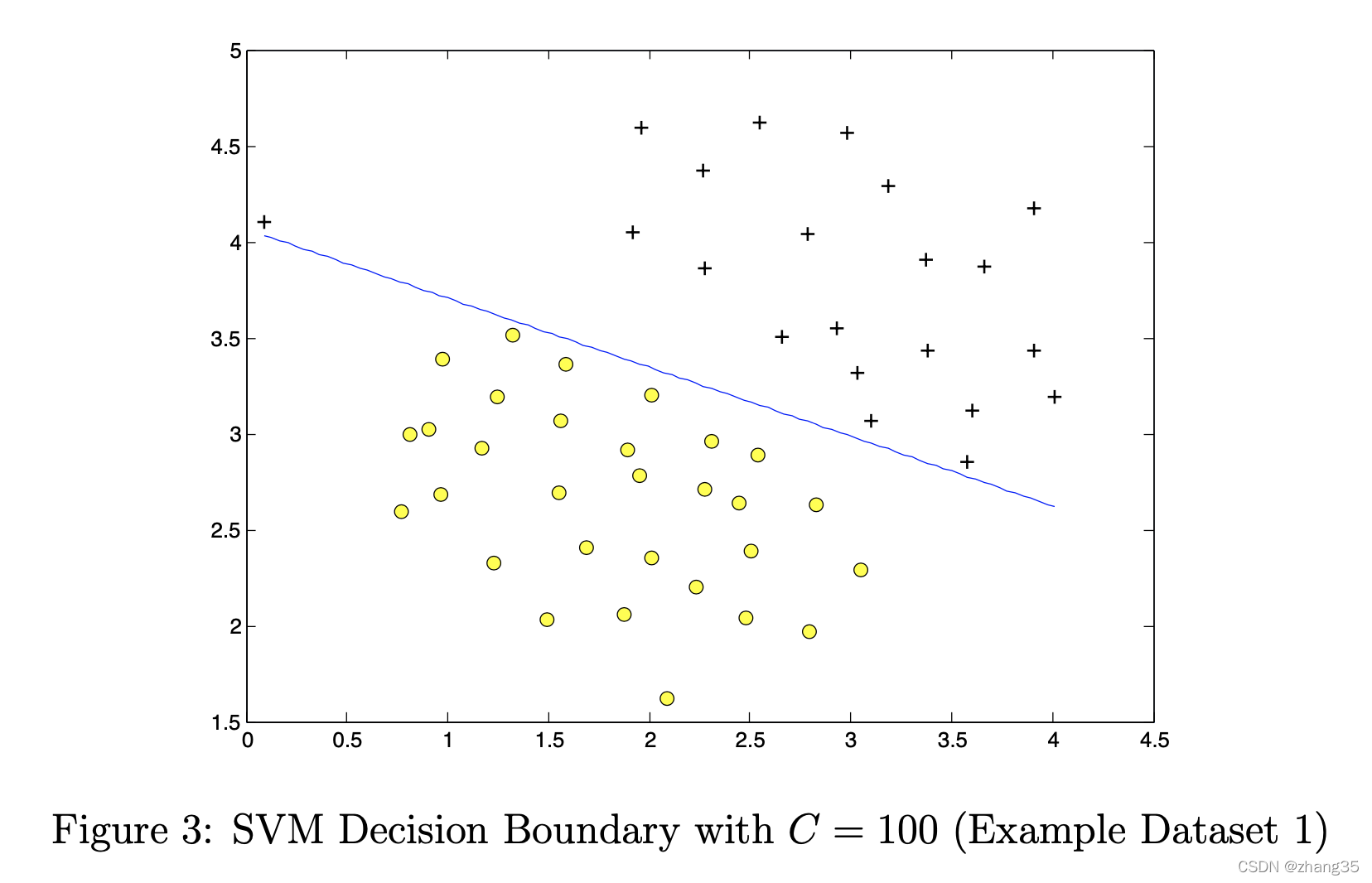
svm决策边界，

核（相似度）函数

SVM擅长解决线性不可分的分类问题。

描述某个样本与标记点的相似度（距离）。相当于映射到一个更高的维度。

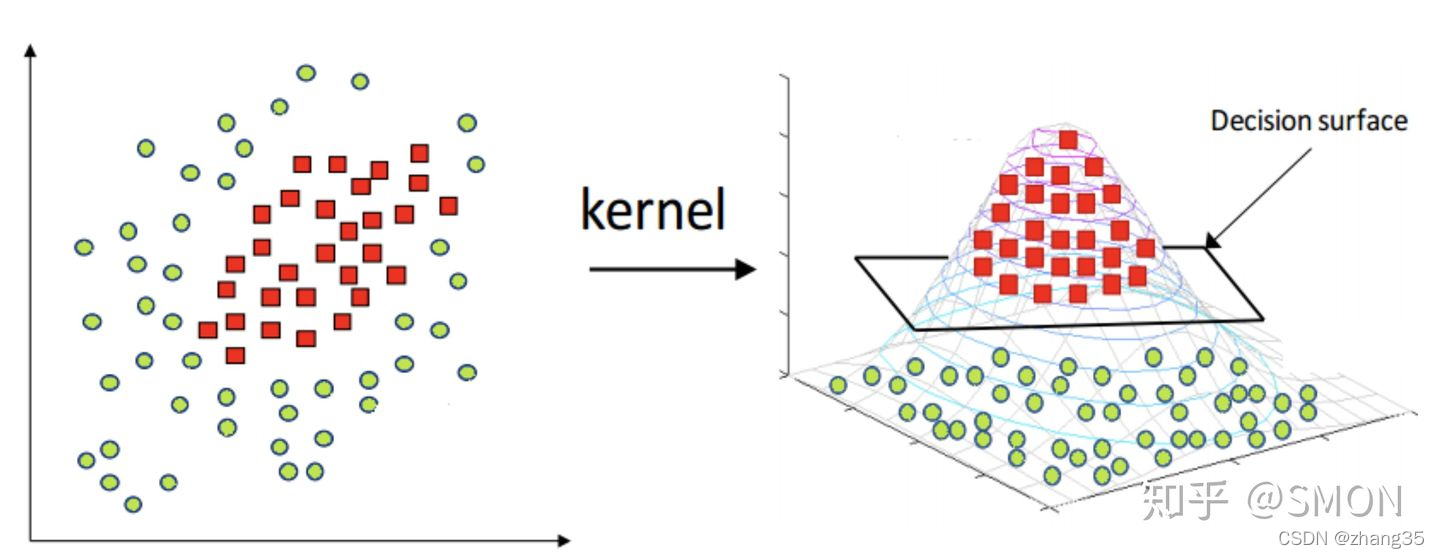
高斯核函数

高斯核函数用来测量一对样本的距离，例如（xi, xj)的距离。

核函数表示样本点与标记点之间距离（相似度）：

σ决定了当样本对距离边远时，相似度衡量函数的下降速度。

σ越大，坡度越平缓，下降越慢：

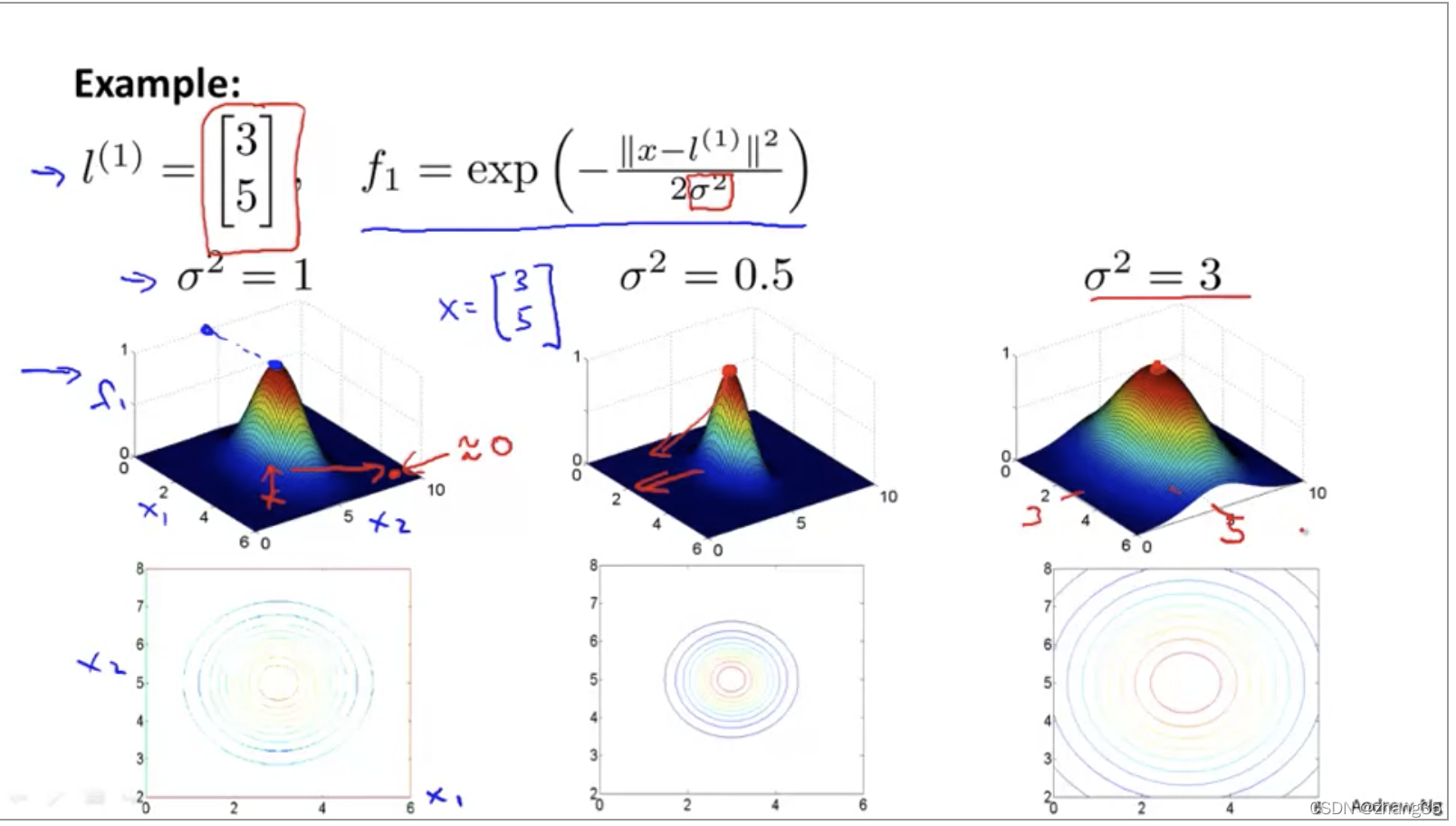
离标记点i越近，f_i就约等于1，离得越远就为0。下图中，红圈内的预测1，外的预测0：

如何选标记点？将所有训练集的点都视作标记点：

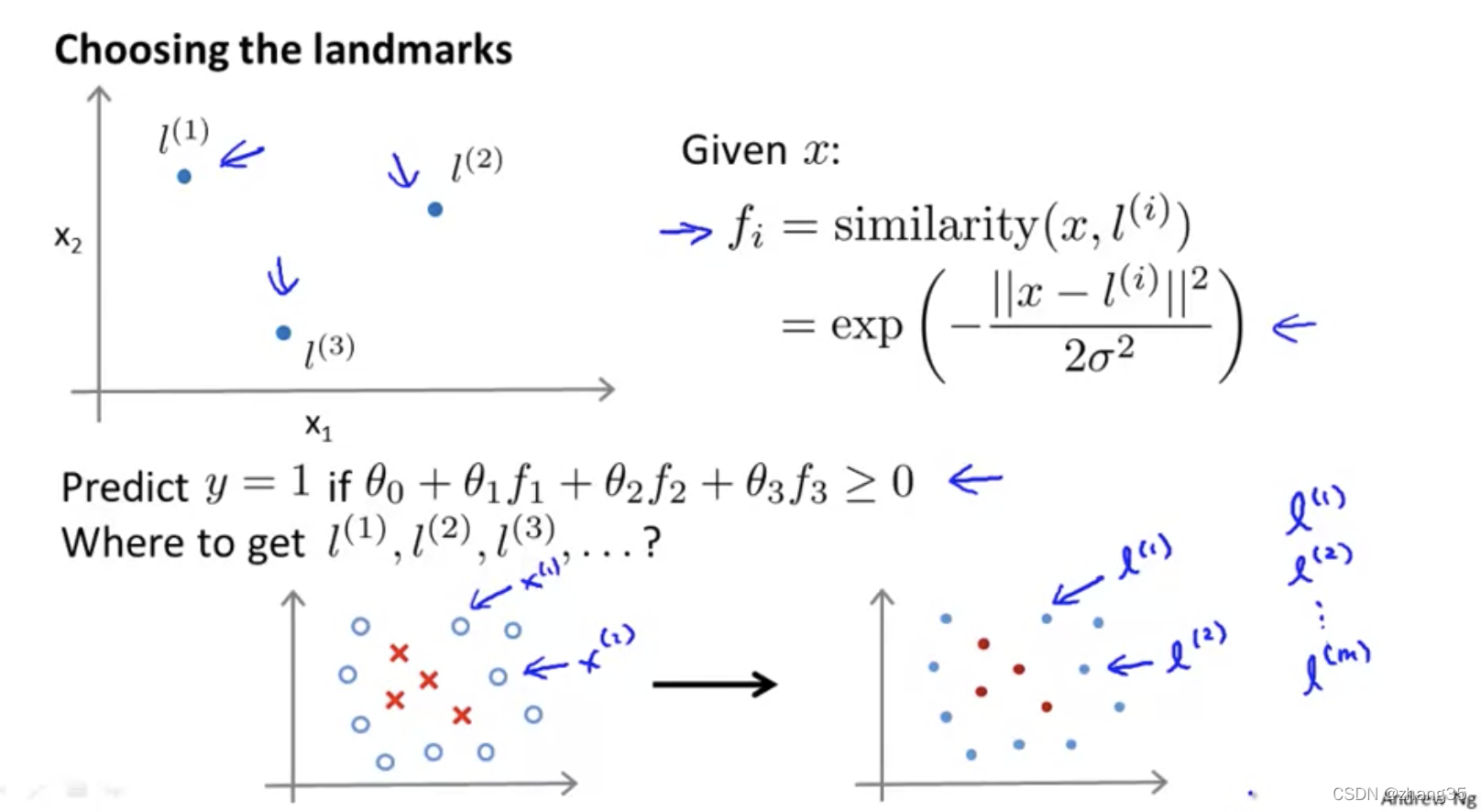
其中

SVM参数

C代表对错误分类的惩罚。相当于λ的倒数。
C越大，偏差越小，方差越大；
C越小，偏差越大，方差越小；

使用SVM的步骤

1. 选择参数C
2. 选择核函数
   当没有核函数的时候，就变成了线性回归问题。也可以认为这时用的是线性核函数。
   如果选了高斯核函数，就需要选择参数σ。
   

注意：要先做scaling

多分类问题

1. 许多SVM包已经包含了多分类功能
2. 也可以用one-vs-all方法
   

SVM优缺点

支持向量机的优点是:

• 由于SVM是一个凸优化问题，所以求得的解一定是全局最优而不是局部最优。
• 不仅适用于线性线性问题还适用于非线性问题(用核技巧)。
• 拥有高维样本空间的数据也能用SVM，这是因为数据集的复杂度只取决于支持向量而不是数据集的维度，这在某种意义上避免了“维数灾难”。
• 理论基础比较完善(例如神经网络就更像一个黑盒子)。

支持向量机的缺点是:

• 二次规划问题求解将涉及m阶矩阵的计算(m为样本的个数), 因此SVM不适用于超大数据集。(SMO算法可以缓解这个问题)
• 只适用于二分类问题。(SVM的推广SVR也适用于回归问题；可以通过多个SVM的组合来解决多分类问题)

SVM vs 逻辑回归 vs 神经网络

怎么选方法？

作业

gaussianKernel.m

function sim = gaussianKernel(x1, x2, sigma)
%RBFKERNEL returns a radial basis function kernel between x1 and x2
%   sim = gaussianKernel(x1, x2) returns a gaussian kernel between x1 and x2
%   and returns the value in sim

% Ensure that x1 and x2 are column vectors
x1 = x1(:); x2 = x2(:);

% You need to return the following variables correctly.
% sim = 0;

% ====================== YOUR CODE HERE ======================
% Instructions: Fill in this function to return the similarity between x1
%               and x2 computed using a Gaussian kernel with bandwidth
%               sigma
%
%

sim = exp(-sum((x1 - x2).^2)/(2*sigma^2));




% =============================================================
    
end

dataset3Params.m

这里注意两处语法：

1. 类似python的for … in … 遍历列表：

varList = [0.01, 0.03, 0.1, 0.3, 1, 3, 10, 30];
for C = varList,
    for sigma = varList,
    ...

2. 函数作为参数时，表示参数的方式：

model = svmTrain(X, y, C, @(x1, x2) gaussianKernel(x1, x2, sigma));

dataset3Params.m：

function [</