优先算法专题十六——BFS解决最短路径问题

最新推荐文章于 2025-12-27 16:49:17 发布

原创最新推荐文章于 2025-12-27 16:49:17 发布 · 339 阅读

4 ·

CC 4.0 BY-SA版权

文章标签：

#宽度优先 #算法

算法专栏收录该内容

12 篇文章

订阅专栏

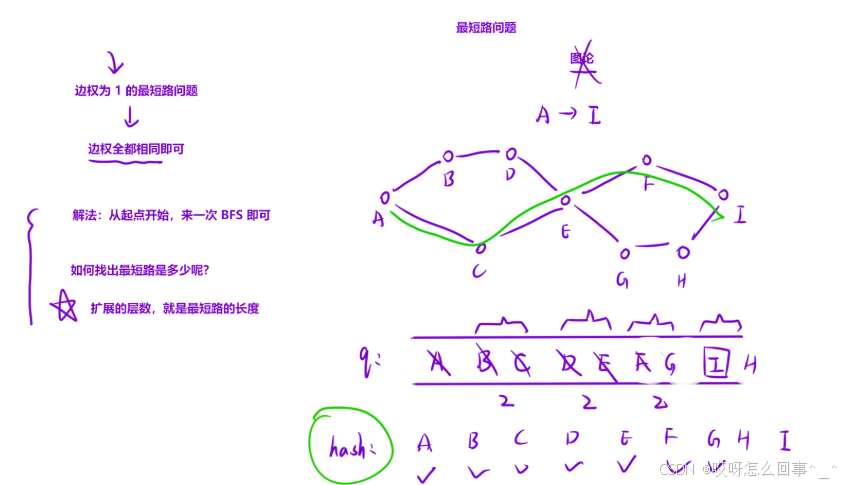
概述：最短路径问题就是边权为一的路径问题，每一次往外走一步步数加上边权，走到目的地步数最少的就是最短路。这种问题一般需要层次遍历来进行辅助，因为层次遍历可以找出本层连接的下一层的地点；一般还要有个哈希表记录地点访问过没有，防止走重复的路。

1926. 迷宫中离入口最近的出口 - 力扣（LeetCode）

每次向外扩展一层，扩展之前提前让总步数加一（下一次向外扩展），若是在下一次扩展中找到了出口就直接返回

class Solution {
public:
    vector<int> dx = {0, 0, -1, 1};
    vector<int> dy = {-1, 1, 0, 0};
    vector<vector<bool>> vis{100, vector<bool>(100, false)};

    int nearestExit(vector<vector<char>>& maze, vector<int>& entrance) {
        int n = maze.size(), m = maze[0].size();
        int ans = 0;
        queue<pair<int, int>> myq;

        myq.push({entrance[0], entrance[1]});
        vis[entrance[0]][entrance[1]] = true;
        while(myq.size())
        {
            ans++;
            //开始向外扩展一层
            int size = myq.size();
            for(int i = 0; i < size; i++)
            {
                auto [a, b] = myq.front();
                myq.pop();
                for(int k = 0; k < 4; k++)
                {
                    int x = a + dx[k], y = b + dy[k];
                    if(x >= 0 && x < n && y >= 0 && y < m && !vis[x][y] && maze[x][y] == '.')
                    {
                        if(x == 0 || x == n - 1 || y == 0 || y == m - 1) return ans;

                        myq.push({x, y});
                        vis[x][y] = true;
                    }
                }
            }
        }
        return -1;
    }
};

433. 最小基因变化 - 力扣（LeetCode）

新增用法：在unordered_map和unordered_set中取一个用，若是不需要映射值就用unordered_set

思路：

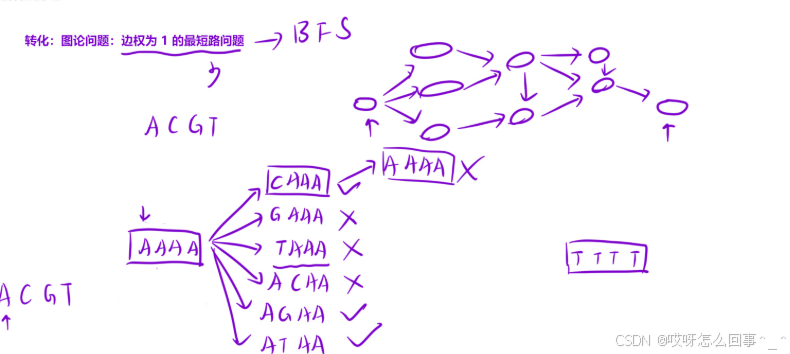
//将问题转换为BFS解决最短路径问题
//由最开始的基因序列一层层扩展查找，每一次扩展的内容为这个基因序列变化的所有可能
//由一个队列记录某一次扩展的基因序列
//只有之前没有被扩展（若是之前已经扩展过再加入队列，那么就重复扩展了，这条路上一定不是最小的次数）的并且在bank里面的才会入队列

class Solution {
public:

    int minMutation(string startGene, string endGene, vector<string>& bank) 
    {
        int ans = 0;//最终结果

        unordered_set<string> hash_bank(bank.begin(), bank.end()), hash_search;//方便查看某个序列在不在bank内、查看某个序列是否被遍历过
            
        if(startGene == endGene) return ans;
        if(hash_bank.find(endGene) == hash_bank.end()) return -1;//最终结果本身不在

        queue<string> myq;
        myq.push(startGene);
        hash_search.insert(startGene);

        char genes[4] = {'A', 'G', 'C', 'T'};
        while(myq.size())
        {
            ans++;//准备开始下一次扩展
            int size = myq.size();
            while(size--)//将上一次的序列全部扩展完
            {
                string str = myq.front();//将此序列变化，扩展
                myq.pop();
                for(int i = 0; i < str.size(); i++)
                {
                    char origin = str[i];
                    for(auto& gene : genes)
                    {
                        if(gene == origin)
                            continue;//跳过原来的字符串
                        string next = str;
                        next[i] = gene;//扩展字符串

                        //先判断是不是结果字符串,因为之前判断了endGene在不在bank中，走到这一定是在。那么只需要判断next和endGene相同与否即可
                        if(endGene == next) return ans;

                        //不是并且没有被访问过并且在bank中就入队列
                        if(hash_bank.find(next) != hash_bank.end() && hash_search.find(next) == hash_search.end())
                        {
                            myq.push(next);
                            hash_search.insert(next);
                        }
                    }
                }
            }
        }
        return -1;
    }
};

127. 单词接龙 - 力扣（LeetCode）

和上题类似

class Solution {
public:
    int ladderLength(string beginWord, string endWord, vector<string>& wordList) {
        if(beginWord == endWord) return 1;//相同直接返回0
        unordered_set<string> hash_list(wordList.begin(), wordList.end());//简化在wordlist里面查找存不存在的过程
        if(hash_list.count(endWord) == 0) return 0;//endWord不存在直接返回0

        unordered_set<string> hash_search;//标记访问过
        hash_search.insert(beginWord);

        queue<string> myq;//层次遍历
        myq.push(beginWord);

        int ans = 1;
        vector<char> words(26, 0);
        for(int i = 0; i < 26; i++)
            words[i] = 'a' + i;
        while(myq.size())
        {
            ans++;
            int size = myq.size();
            while(size--)//一次扩展
            {
                string cur = myq.front();
                myq.pop();
                for(int i = 0; i < cur.size(); i++)
                {
                    char origin = cur[i];
                    for(auto& ch : words)
                    {
                        if(ch == origin) continue;

                        string next = cur; next[i] = ch;
                        if(next == endWord) return ans;
                        //在hash_list里面并且未被访问就进队列并且标记已访问过
                        if(hash_list.count(next) && !hash_search.count(next))
                        {
                            myq.push(next);
                            hash_search.insert(next);
                        }
                    }
                }
            }
        }
        return 0;
    }
};

675. 为高尔夫比赛砍树 - 力扣（LeetCode）

因为题意是按照树的高度进行砍树，所以要找出下一次砍树的坐标，需要先将树的坐标按照树的高度排序；

之后将下棵树的下标作为迷宫问题的终点，起点为上一次的终点开始进行bfs查找

class Solution {
public:
//将这个问题分解为多步的迷宫问题，每次的出口换成了下一次应该砍的树的下标，依次统计步数即可
typedef pair<int, int> PII;
int n, m;
    int cutOffTree(vector<vector<int>>& forest) 
    {
        n = forest.size();
        m = forest[0].size();
        //首先将砍的树的下标按照树的高度排序
        vector<PII> sortindex;
        for(int i = 0; i < n; i++)
            for(int j = 0; j < m; j++)
                if(forest[i][j] > 1) sortindex.push_back({i, j});
        sort(sortindex.begin(), sortindex.end(), [&](const PII& xy1, const PII xy2)->bool{
            return forest[xy1.first][xy1.second] < forest[xy2.first][xy2.second];
        });//[&]捕捉forest里面的数

        //多次进行统计寻找下一颗树所需步数的操作
        int ans = 0;
        int bx = 0, by = 0;//起点
        for(auto& [a, b] : sortindex)
        {
            int ret = bfs(forest, bx, by, a, b);
            if(ret == -1) return -1;//说明下一棵树的位置到不了
            ans += ret;
            //下一次寻找的起点为上一次寻找的终点
            bx = a;
            by = b;
        }
        return ans;
    }
int dx[4] = {0, 0, 1, -1};
int dy[4] = {1, -1, 0, 0};
bool vis[51][51] = {false};//避免重复回走
    int bfs(vector<vector<int>>& forest, int bx, int by, int ex, int ey)
    {
        if(bx == ex && by == ey) return 0;

        memset(vis, false, sizeof vis);//每一次都是新的查找，所以要重新标记
        int ret = 0;
        queue<PII> q;
        q.push({bx, by});
        vis[bx][by] = true;

        while(q.size())
        {
            ret++;
            int sz = q.size();
            while(sz--)
            {
                auto [a, b] = q.front();
                q.pop();
                for(int i = 0; i < 4; i++)
                {
                    int x = a + dx[i], y = b+ dy[i];

                    if(x == ex && y == ey) return ret;

                    if(x >= 0 && x < n && y >= 0 && y < m && !vis[x][y] && forest[x][y] != 0)
                    {
                        q.push({x, y});
                        vis[x][y] = true;
                    }
                }
            }
        }
        return  -1;
    }
};