一、概念
- AVL树基于二叉搜索树;要么是空树,要么是一颗每个节点的左右子树的高度差都不超过一的二叉搜索树;
- AVL树引入平衡因子(balance factor),这个平衡因子是每个节点的属性,它的值等于当前节点的右子树高度减去左子树的高度;
- 不设计成相差0就是AVL树的原因:当节点数是2时,根节点的左右子树高度差为1,这种情况下做不到高度差为0;
- AVL树结构和完全二叉树相近,查找的时间复杂度在O(logN)。
二、AVL树的插入
1、插入叙述:
- AVL树类中私有成员变量是一个根节点,初始化为空指针;插入的第一个值用来给这个根节点;后面插入的值先通过和二叉搜索树一样的查找,找到插入的位置节点(也就是新节点的父节点),判断新节点的值是大于还是小于父节点,再判断让父节点的左指针还是右指针指向新节点;AVL树设计成三叉链的结构,每一个节点的成员变量除了有左右节点指针还有一个父节点指针;所以再插入之后还要将新节点的父节点指针指向父节点;
- 插入并且链接完成之后要更新平衡因子;进入循环(通过每个节点的父节点指针向上调整)首先是当前的父节点(也是最底部的),看新节点插入的是它的左边还是右边,是右边就让它的平衡因子加加,反之减减;之后这个父节点的平衡因子若是0,那么就更新完了,说明上面的节点的左右子树高度差没有被影响;若父节点的平衡因子是-1或者1,那么目前的这颗小树的高度变化了,说明上面节点的左右子树的高度差发生了变化,需要继续向上更新,此时通过父节点指针向上遍历;若是2或者-2就要旋转;不可能是其他的情况了,因为其他的情况出现了说明插入之前就不是AVL树;
- 旋转:旋转是一种调节,旋转是为了让这棵树平衡,旋转不会破坏AVL树的规则,旋转之后的平衡因子也是正确的;旋转的触发条件是当前父节点的平衡因子是2或者-2;旋转有四种:左单旋、右单旋,左右双旋、右左双旋;
2、旋转解析:
旋转的代码写出是根据图形来的;
1、右单旋:
单旋就是单纯的一边高(父节点是右边高并且当前节点也是右边高(或者都是左边))
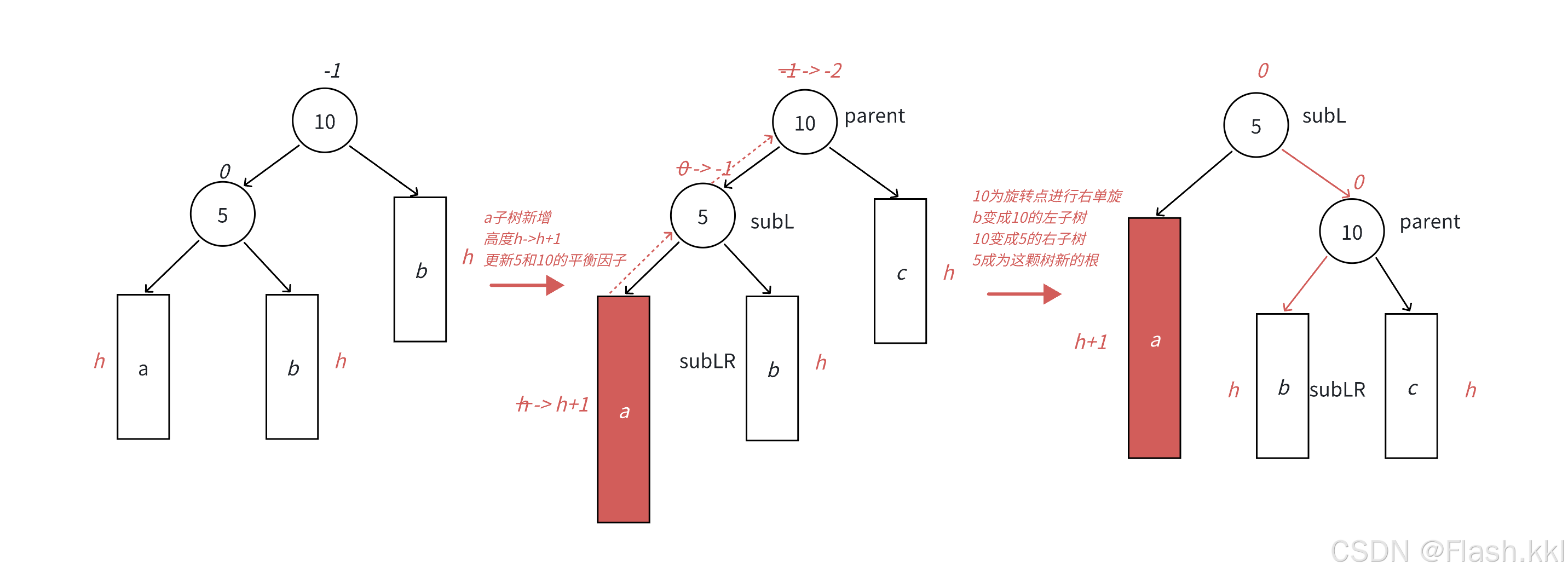
插入的是a,更新到10这个节点时,10这个节点就是当前父节点,它的平衡因子是2,需要旋转来调节;
首先将5这个节点的右子树给10这个节点的左子树,再把10这个节点给5的右子树;之后让5这个节点的父节点指针和10这个节点的父节点链接。
最后将10和5这两个节点的平衡因子手动置为0,其他的节点的额平衡因子在之前就更新好了并且在旋转后没有发生变化;右旋结束。
2、左单旋:
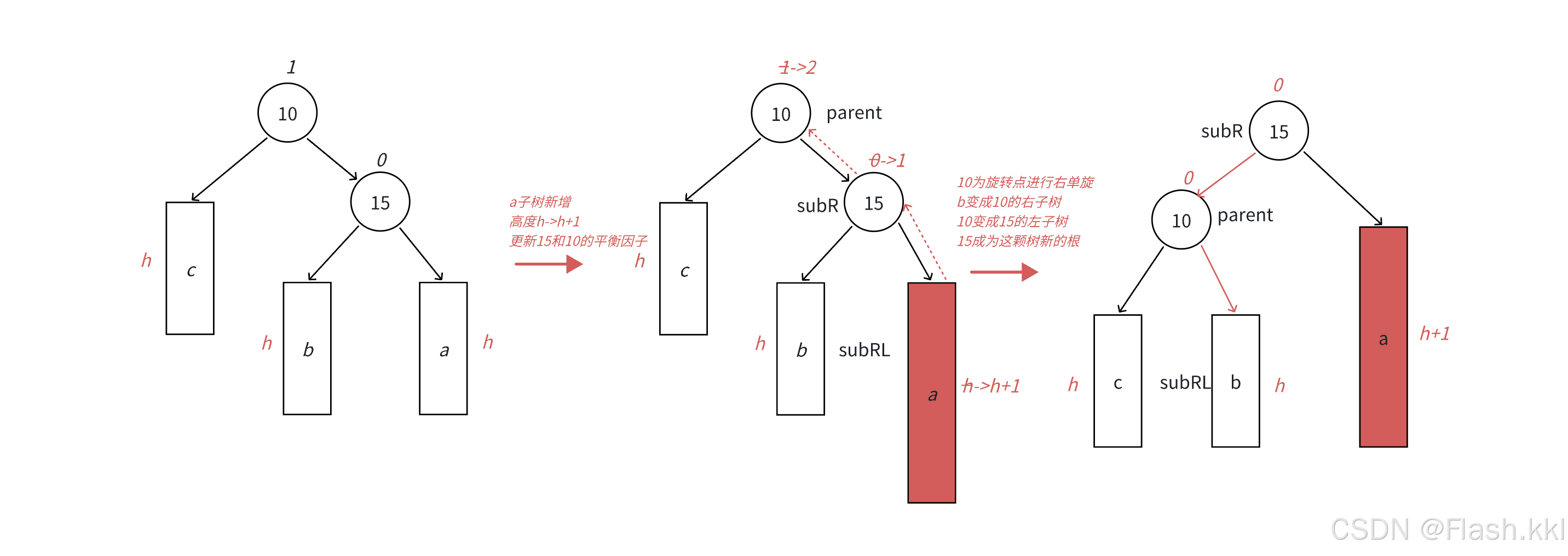
左单旋和有单旋类似;
3、左右双旋:
双旋不是单纯的一边高(父节点是左边高但是当前节点是右边高(或者相反))
触发旋转后,当父节点的平衡因子和当前节点的平衡因子异号时需要双旋,之前的单旋解决不了问题,只会将右边的变为左边,或者左边变为右边,没有解决父节点左右子树高度差超过一的问题;
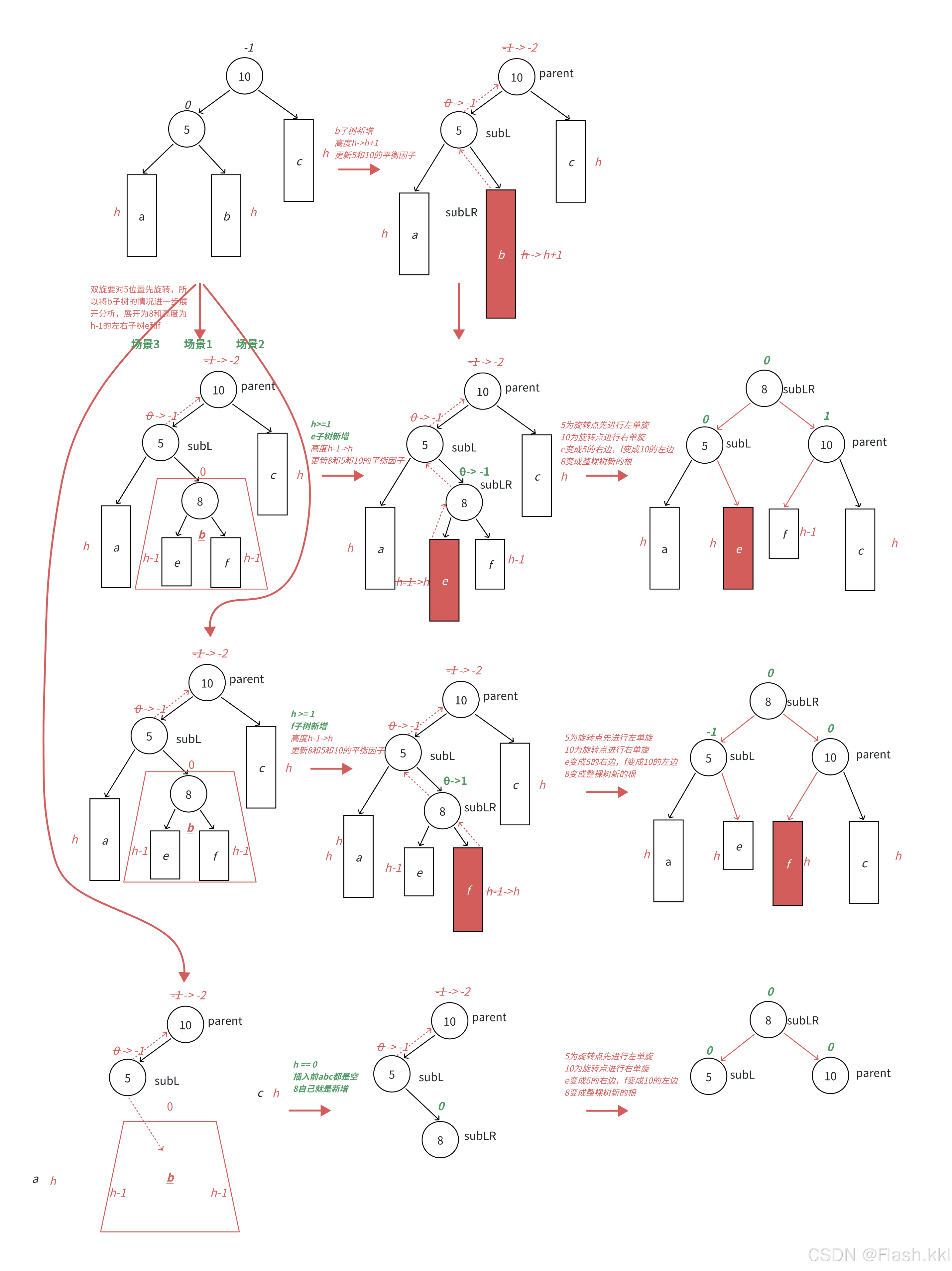
先将当前节点作为一个父节点进行左旋,之后再让当前节点的父节点右旋;这里复用了单旋的代码;
但是双旋完之后会三种情况(也就是双旋完之后三个节点的平衡因子的手动置给的值会右三种情况),这三种情况的产生是因为插入的情况不同(上图)
就拿这个图为例子:
先看图中前两个旋转:e和f的位置最终是固定的,当插入到e时,e的父节点的平衡因子是一种情况,但是插入到f时,e的父节点的平衡因子又是另外一种情况,而这种差异的产生是因为插入的位置不同,也就是当前节点的右子树根节点的平衡因子的不同;当a、b、c都是空时插入新节点又是另一张情况,也就是第三个旋转,最后所有节点平衡因子都是0;
为了解决这个问题,需要提前记录当前节点的的右子树节点的平衡因子(单旋会改变这个节点的平衡因子,不记录最后判断有误),旋转完之后,通过判断这个平衡因子的不同来手动给这三个关键节点的平衡因子置值,其他的节点的平衡因子没有变化;
4、右左双旋:
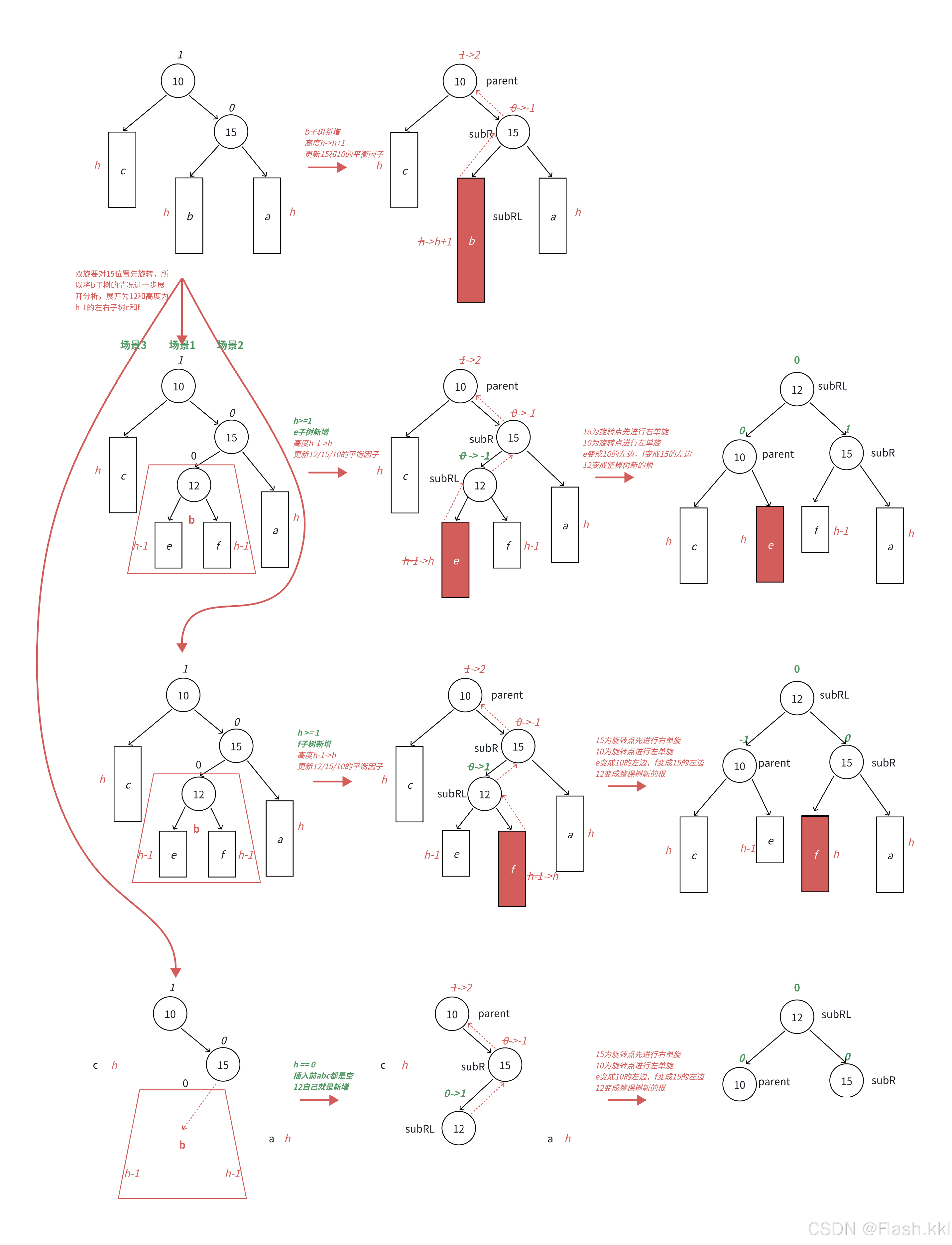
和左右双旋类似;
三、具体代码:
#include<iostream>
#include<assert.h>
#include<vector>
using namespace std;
template<class T>
struct AVLTreeNode
{
AVLTreeNode(const T& data = T())
: _pLeft(nullptr)
, _pRight(nullptr)
, _pParent(nullptr)
, _data(data)
, _bf(0)
{}
AVLTreeNode<T>* _pLeft;
AVLTreeNode<T>* _pRight;
AVLTreeNode<T>* _pParent;
T _data;
int _bf; // 节点的平衡因子
};
// AVL: 二叉搜索树 + 平衡因子的限制
template<class T>
class AVLTree
{
typedef AVLTreeNode<T> Node;
public:
AVLTree()
: _pRoot(nullptr)
{}
// 在AVL树中插入值为data的节点
bool Insert(const T& data)
{
if (_pRoot == nullptr)
{
_pRoot = new Node(data);
return true;
}
Node* pParent = nullptr;
Node* cur = _pRoot;
while (cur)
{
if (data > cur->_data)
{
pParent = cur;
cur = cur->_pRight;
}
else if (data < cur->_data)
{
pParent = cur;
cur = cur->_pLeft;
}
else
{
return false;//相同就返回假,插入失败了
}
}
//出循环找到了插入的位置(即插入之后的父节点)
cur = new Node(data);
cur->_pParent = pParent;//链接父亲
if (data > pParent->_data)
{
pParent->_pRight = cur;
}
else
{
pParent->_pLeft = cur;
}
//插入完成之后更新平衡因子
while (pParent)
{
if (pParent->_pLeft == cur)
{
pParent->_bf--;
}
else
{
pParent->_bf++;
}
if (pParent->_bf == 0)
{
break;
}
else if (pParent->_bf == -1 || pParent->_bf == 1)
{
cur = pParent;
pParent = pParent->_pParent;
}
else if (pParent->_bf == 2 || pParent->_bf == -2)
{
if (pParent->_bf == -2 && cur->_bf == -1)
{
// 右单旋
RotateR(pParent);
}
else if (pParent->_bf == 2 && cur->_bf == 1)
{
// 左单旋
RotateL(pParent);
}
else if (pParent->_bf == 2 && cur->_bf == -1)
{
// 右左双旋
RotateRL(pParent);
}
else if (pParent->_bf == -2 && cur->_bf == 1)
{
// 左右双旋
RotateLR(pParent);
}
else
{
assert(false);
}
break;//没有走else就说明是正常情况,那么最后会走 break
}
else
{
//平衡因子有问题
assert(false);
}
}
return true;
}
Node* Find(const T& data)
{
Node* cur = _pRoot;
while (cur)
{
if (data > cur->_data)
{
cur = cur->_pRight;
}
else if (data < cur->_data)
{
cur = cur->_pLeft;
}
else
{
return cur;
}
}
return nullptr;
}
// AVL树的验证
bool IsAVLTree()
{
return _IsAVLTree(_pRoot);
}
size_t Height()
{
return _Height(_pRoot);
}
void Inorder()
{
_Inorder(_pRoot);
cout << endl;
}
size_t Size()
{
return _Size(_pRoot);
}
private:
// 根据AVL树的概念验证pRoot是否为有效的AVL树
bool _IsAVLTree(Node* pRoot)
{
if (pRoot == nullptr)
{
return true;
}
size_t L = _Height(pRoot->_pLeft);
size_t R = _Height(pRoot->_pRight);
int differ = (int)(R - L);
if (abs(differ) > 1)
{
cout << "The tree is not an AVLTree." << endl;
return false;
}
if (pRoot->_bf != differ)
{
cout << "The bf is wrong." <<endl;
return false;
}
return _IsAVLTree(pRoot->_pLeft) && _IsAVLTree(pRoot->_pRight);
}
size_t _Height(Node* pRoot)
{
if (pRoot == nullptr)
{
return 0;
}
size_t L = _Height(pRoot->_pLeft);
size_t R = _Height(pRoot->_pRight);
return (L > R ? L : R) + 1;
}
size_t _Size(Node* pRoot)
{
if (pRoot == nullptr)
{
return 0;
}
return _Size(pRoot->_pLeft) + _Size(pRoot->_pRight) + 1;
}
void _Inorder(Node* pRoot)
{
if (pRoot == nullptr)
{
return;
}
_Inorder(pRoot->_pLeft);
cout << pRoot->_data << " ";
_Inorder(pRoot->_pRight);
}
// 右单旋
void RotateR(Node* pParent)
{
Node* subl = pParent->_pLeft;
Node* sublr = subl->_pRight;
pParent->_pLeft = sublr;
if (sublr)
sublr->_pParent = pParent;
Node* p_pParent = pParent->_pParent;//提前记录下父节点的父节点
subl->_pRight = pParent;
pParent->_pParent = subl;
if (pParent == _pRoot)
{
_pRoot = subl;
subl->_pParent = nullptr;
}
else
{
if (p_pParent->_pLeft == pParent)
{
p_pParent->_pLeft = subl;
subl->_pParent = p_pParent;
}
else
{
p_pParent->_pRight = subl;
subl->_pParent = p_pParent;
}
}
pParent->_bf = subl->_bf = 0;
}
// 左单旋
void RotateL(Node* pParent)
{
Node* subr = pParent->_pRight;
Node* subrl = subr->_pLeft;
pParent->_pRight = subrl;
if (subrl)
subrl->_pParent = pParent;
Node* p_pParent = pParent->_pParent;//提前记录
subr->_pLeft = pParent;
pParent->_pParent = subr;
if (pParent==_pRoot)
{
_pRoot = subr;
subr->_pParent = nullptr;
}
else
{
if (p_pParent->_pLeft == pParent)
{
p_pParent->_pLeft = subr;
subr->_pParent = p_pParent;
}
else
{
p_pParent->_pRight = subr;
subr->_pParent = p_pParent;
}
}
pParent->_bf = subr->_bf = 0;
}
// 右左双旋
void RotateRL(Node* pParent)
{
Node* subr = pParent->_pRight;
Node* subrl = subr->_pLeft;
int bf = subrl->_bf;//提前记录一份,因为单旋会改变
RotateR(subr);
RotateL(pParent);
//旋转完之后是AVL,但是平衡因子会不匹配
if (bf == -1)
{
pParent->_bf = 0;
subr->_bf = 1;
subrl->_bf = 0;
}
else if (bf == 1)
{
pParent->_bf = -1;
subr->_bf = 0;
subrl->_bf = 0;
}
else if (bf == 0)
{
pParent->_bf = 0;
subr->_bf = 0;
subrl->_bf = 0;
}
else
assert(false);
}
// 左右双旋
void RotateLR(Node* pParent)
{
Node* subl = pParent->_pLeft;
Node* sublr = subl->_pRight;
int bf = sublr->_bf;
RotateL(subl);
RotateR(pParent);
if (bf == -1)
{
pParent->_bf = 1;
subl->_bf = 0;
sublr->_bf = 0;
}
else if (bf == 1)
{
pParent->_bf = 0;
subl->_bf = -1;
sublr->_bf = 0;
}
else if (bf == 0)
{
pParent->_bf = 0;
subl->_bf = 0;
sublr->_bf = 0;
}
else
assert(false);
}
private:
Node* _pRoot;
};
关键是记下图来;





















 1418
1418

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








