论文笔记：Efficient Multi-Stage Video Denoising with Recurrent Spatio-Temporal Fusion

这是Huawei Noah‘s Ark Lab在CVPR2021上的文章。他们针对于终端设备算力有限的条件下，提出了一种有效的视频降噪算法EMVD，其主要特点在于

1. 通过可学习的可逆变换，将图像的亮度和颜色信息，以及不同的频率信息进行分解，在变换域进行图像降噪处理；
2. 使用了三级结构，包括时域融合（temporal fusion）、空域降噪（spatial denoising）、时空精修（spatio-temporal refinement）三个阶段，每级结构都有明确的任务和可解释性；
3. 使用很小的参数和计算量就可以取得较好的效果；

Overview

降噪方法针对于RAW域图像，假设噪声模型是异质性高斯噪声，即由读出噪声和散粒噪声构成。

${\sigma }_t^2(y_t)=a_t{y}_t+b_t$

在这种假设下，噪声参数$a_t$和$b_t$只与给定的传感器和相机ISO参数有关，因而可以提前进行噪声标定获得噪声参数。

整个方法流程图如下图所示

Learnable Invertible Transforms

受YUV和小波变换的启发，可以将RAW图像的颜色信息和频率信息做分解，这种变换是线性且可逆的，可以通过设计为标准卷积操作来学习。

其中颜色变换可以设计为$1\times 1$卷积，输入4通道（RGGB），输出4通道；通常颜色矩阵定义为

$M=\left[\begin{array}{cccc}0.5& 0.5& 0.5& 0.5\\ -0.5& 0.5& 0.5& -0.5\\ 0.65& 0.2784& -0.2784& -0.65\\ -0.2784& 0.65& -0.65& 0.2784\end{array}\right]=\left[\begin{array}{c}Y\\ U\\ V\\ W\end{array}\right]$

在本文中使用该矩阵作为卷积初始化初始化。

频率变换可以像如Haar小波一样，设计为4个$n\times n$的卷积。文章使用两个$1\times n$一维滤波器，包括一个低通滤波${\psi }_L$和一个高通滤波${\psi }_H$。两者相互组合的外积作为$n\times n$的卷积核初始化。

为了保证学习到的正变换和逆变换是相互可逆的，在学习时加入了约束

$L_c=\Vert M\cdot M^{\prime }-I_C{\Vert }_F^2$ 和$L_f=\Vert \psi \cdot \varphi -I_2{\Vert }_F^2$

其中，$I_c$和$I_2$分别为秩为C和2的单位矩阵。

Fusion Stage

该阶段的目的是使用视频的时域相关特征来减小噪声同时不引入其他的伪纹理。因而，时域融合可以定义为

${\bar{y}}_t(x)={\bar{y}}_{t-1}(x){\bar{\gamma }}_{t-1}(x)+z_t(x){\gamma }_t(x)$

其中，$\gamma$是非负的凸权重，通道数为1，且满足${\bar{\gamma }}_{t-1}(x)+{\gamma }_t(x)=1$。在$t=0$时刻初始化${\bar{y}}_0\equiv z_0$。

融合权重使用网络进行估计

{ γ t , γ ˉ t − 1 } = F C N N ( ∣ z L L ∣ t − y ˉ L L ∣ t − 1 ∣ , σ ^ t 2 ) \{\gamma_t,\bar{\gamma}_{t-1}\}=FCNN(|z_{LL|t}-\bar{y}_{LL|t-1}|,\hat{\sigma}^2_t) {γt​,γˉ​t−1​}=FCNN(∣zLL∣t​−yˉ​LL∣t−1​∣,σ^t2​)

其中，$z_{LL|t}$和${\bar{y}}_{LL|t-1}$分别表示噪声输入和上一时刻融合帧的低通分量。${\hat{\sigma }}_t^2={\sigma }_t^2(z_{LL|t})$表示输入帧的噪声方差，此处使用$z_{LL|t}$代表$y_t$来减小噪声对方差估计的影响。FCNN的输出层使用sigmoid函数作为激活函数。当使用多尺度时，低尺度的融合权重也被上采样作为额外的输入，正如方法流程图所示。

时域融合也可以解释为核预测网络的一种核为$1\times 1$的特殊情况。因此时域融合的广义形式可以定义为：

${\bar{y}}_t(x)={\bar{y}}_{t-1}(x)⊛{\bar{k}}_{t-1}(x)+z_t(x)⊛k_t(x)$

其中$⊛$表示卷积操作，$k$表示应用于当前噪声帧大小为$p\times p$的空间自适应核，${\bar{k}}_{t-1}$表示应用于前一帧的大小为$\bar{p}\times \bar{p}$的核。

Denoising Stage

仅仅采用时域融合进行降噪是不充分的，因为图像中的运动区域不能被时域信息有效地补偿。因而，在时域融合之后进行空域降噪。

${\tilde{y}}_t=DCNN({\bar{y}}_t,z_{LL|t},{\bar{\sigma }}_t^2)$

其中，$\overline{{\sigma }_t^2}$是融合图像${\bar{y}}_t$的噪声方差，其不仅依赖于第$t$帧的信号依赖方差，同时也依赖于融合的所有过去帧的累加效应。

${\bar{\sigma }}_t^2\equiv {\sigma }_t^2({\bar{y}}_{LL|t})={\bar{\gamma }}_{t-1}^2{\sigma }_{t-1}^2({\bar{y}}_{LL|t-1})+{\gamma }_t^2{\sigma }_t^2(z_{LL|t})$

其中，视频噪声在时域上认为是独立的，因而去掉了互相关项，且初始化条件为${\sigma }_t^2({\bar{y}}_{LL|0})\equiv {\sigma }_t^2(Z_{LL|0})$。既然${\gamma }_t(x)\le 1$，方差${\bar{\sigma }}_t^2$随时间减小。

当使用多尺度时，低尺度的数据也被上采样作为额外的输入。

Refinement Stage

降噪可能会带来伪纹理和信息丢失，因而在进行降噪之后，加入了精修阶段提升降噪效果。精修阶段通过将融合阶段图像${\bar{y}}_t$（有高频纹理但存在噪声）中的高频信息叠加到降噪阶段输出图像${\tilde{y}}_t$（无噪声但过平滑）上，达到提升图像细节的效果。

${\hat{y}}_t(x)={\bar{y}}_t(x){\bar{\omega }}_t(x)+{\tilde{y}}_t(x){\tilde{\omega }}_t(x)$

其中，凸权重满足${\bar{\omega }}_t(x)+{\tilde{\omega }}_t(x)=1$。精修权重也通过一个网络来进行计算

{ ω ~ t , ω ˉ t } = R C N N ( y ~ t , y ˉ t , σ ˉ t 2 ) \{\tilde{\omega}_t,\bar{\omega}_{t}\}=RCNN(\tilde{y}_t,\bar{y}_{t},\bar{\sigma}^2_t) {ω~t​,ωˉt​}=RCNN(y~​t​,yˉ​t​,σˉt2​)

同样，RCNN的输出层使用sigmoid函数作为激活函数。而且精修网络仅仅在最高的尺度上进行。

Experiment

数据集

CRVD Benchmark 其包括了一个利用SONY IMX385传感器拍摄的真实RAW视频数据集（CRVD）和一个合成数据集SRVD。所有视频有五个不同的ISO水平，ISO范围为[1600,25600]。文章使用完整的SRVD加上CRVD的1-6场景作为训练集，CRVD的7-11场景作为验证集。CRVD也包含了少量没有GT的户外噪声视频作为视觉质量比较。

IMX327 Dataset 使用SONY IMX327传感器拍摄了更多的图像。使用1042张高质量RAW图合成训练集，ISO从25600到96000取值。验证集包含了6个合成噪声视频，ISO分别为25600,51200和96000。测试集使用了6个在低照度场景（1l ux以下）下拍摄的真实噪声视频。

训练

在合成IMX327数据集时，通过合成随机运动轨迹从单帧图像上进行裁剪，从而模拟不同的位移。在生成长序列数据时，可以通过将每个序列进行时间反转叠加起来。训练损失函数定义为$L=L_r+L_c+L_f$。其中$L_r$定义为$L_1$损失。

消融实验

下表展示了不同的消融实验在CRVD上测试的结果。

实验说明了在降噪阶段分配更多的参数和算力是更有效的。下表展示了时域融合阶段使用不同核大小对结果的影响。

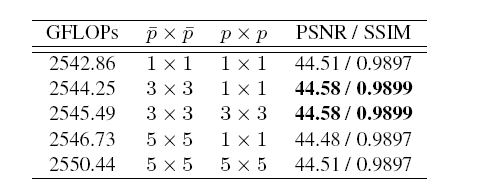
可以观察到对以前帧使用更大的核有利于运动补偿，从而得到更好的结果。

实验结果

左图展示了不同方法的运算开销和结果指标之间的相对关系，可以看出EMVD在比较小的计算量的条件下能取得更好的性能。右图展示了使用更多的输入帧对结果的影响。其他使用多帧输入的方法在经过初始的帧数增加后达到一个稳定的水平，而EMVD是使用递归的方法，因而积累长时间的信息更加有利。

下表展示了在Huawei P40 Pro手机芯片上，处理单精度720p视频序列的测试结果。可以看到EMVD可以实现接近30fps的处理速度。

Conclusion

本文提出了一种多阶段的视频降噪的方法EMVD。其最大的特点在于其可解释性和高效性。对于每一阶段的功能和效果都能给予解释和分析，整体的算法可以有效地应用于终端设备中，实现落地应用。