论文笔记：ROBUST AND INTERPRETABLE BLIND IMAGE DENOISING VIA BIAS-FREE CONVOLUTIONAL NEURAL NETWORKS

这是ICLR 2020的一篇文章，单位为纽约大学。其主要讨论了通过将网络结构中的所有加性参数去掉，得到无偏置网络（bias-free network）可以在不同的噪声水平下有更好的泛化性能，即使其只在一个非常小的的噪声水平上做训练。对于无偏置网络来说，每个局部位置都可以将网络权重看做是一个滤波器，其自适应于图像结构和噪声水平。

NETWORK BIAS IMPAIRS GENERALIZATION

假设噪声图像包含加性噪声：$y=x+n$，而且噪声$n$是独立同分布的高斯白噪声，方差为${\sigma }^2$。

当使用神经网络进行降噪时，由于$\sigma$未知（盲去噪），因而网络需要对噪声水平有一定的泛化性能，特别是当测试的噪声水平不包含在训练集中时。

使用ReLUs的前馈神经网络是分段仿射的（piecewise affine）。对于一个固定的噪声输入$y$，神经网络拟合的降噪函数$f(\cdot )$可以表示为：

$$f(y)=W_{L}R(W_{L-1}...R(W_{1}y+b_1)+...b_{L-1})+B_L=A_{y}y+b_y$$

其中，$W_k$表示线性变换（卷积或全连接层，$k$s是网络层数），$b_k$表示加性偏置，$R$表示固定的激活图样。

$A_y$是$f(\cdot )$相对于输入$y$的雅可比矩阵（Jacobian）,$b_y$表示网络偏置（net bias）。他们都依赖于ReLU的激活图样，从而依赖于输入$y$。

下图展示了使用不同噪声水平范围的训练集得到的结果。CNN使用DnCNN结构。

图 1

可以看到，当网络在整个噪声水平范围上做训练时，网络偏置整体都是比较小的，随着噪声增加略微有增长。这说明了线性项（$W_k$）在降噪中起到更大的作用。当网络在一个更小的噪声范围内做训练时，网络偏置会在噪声水平超出训练范围后突然增大。这说明此时网络已经出现过拟合了，因而对超出训练范围的噪声水平泛化性能下降。

PROPOSED METHODOLOGY: BIAS-FREE NETWORKS

通过上面的观察，可以通过去除加性偏置项来改善网络的过拟合，提升泛化性能。因而文章提出了无偏执CNN（bias-free CNN，BF-CNN），就是将网络中各个阶段的偏置项（包括BN层中的偏置项）全部去掉。而这会使得使用ReLU的前馈神经网络具有缩放不变性，即输入经过一个常数缩放等于网络输出经过相同常数的缩放。

引理 1. 令$f_{BF}:R^N\to R^N$是一个使用ReLU作为激活函数的前馈神经网络，且在任何层中都没有加性常数项。对于任意输入$y\in R$和任意非负常数$\alpha$，都有

$f_{BF}(\alpha y)=\alpha f_{BF}(y)$。

上述引理对于有并联或加性跳跃连接的网络同样适用，他们都是线性操作。

下图展示了BF-CNN和传统CNN的降噪性能的比较。两者使用了相同的网络结构（DnCNN）。可以看到BF-CNN在训练范围外有更好的泛化性能。

图2

文章测试了包括DnCNN，Recurrent CNN，UNet，Simplified DenseNet四种网络结构。不同的网络结构都能得到相似的现象，原始有偏置的CNN都在训练范围内取得好的性能，但是在新的噪声水平上出现明显下降。而对应的BF-CNN都在不同的噪声范围中体现了好的泛化性能。

从左到右依次为DnCNN、Recurrent CNN、UNet、DenseNet 图3

REVEALING THE DENOISING MECHANISMS LEARNED BY BF-CNNS

一个无偏置网络是局部线性的，可以表示为

$$f_{BF}(y)=W_{L}R(W_{L-1}...R(W_{1}y))=A_{y}y$$

对于固定输入的雅可比矩阵$A_y$展示了去噪图的局部特性。

局部自适应滤波

输出图像的第$i$个像素可以使用$A_y$第$i$行（$a_y(i)$）与输入图像的内积计算得到：

$f_{BF}(y)(i)={\sum }_{j=1}^N{A}_y(i,j)y(j)=a_y(i{)}^{T}y$

向量$a_y(i)$可以解释为自适应滤波器，其通过对噪声像素进行加权平均得到去噪像素。

下图展示了一个BF-CNN中线性加权函数（向量$a_y(i)$）的可视化结果。

图4

可以看出这些权重是自适应于图像的局部特征，只对均质区域进行加权平均而避免模糊边缘。而且可以看到，随着噪声水平$\sigma$增大，权重函数的空间延伸也在增大。不同像素位置的权重函数大不相同。

自适应低维子空间的投影

对一个给定的输入$y$，计算雅克比矩阵的SVD分解$A_y=US{V}^T$，可得到

$f_{BF}(y)=A_{y}y=US{V}^{T}y={\sum }_{i=1}^N{s}_i(V_i^{T}y)U_i$

输出是左奇异向量的线性组合。每个向量的权重由输入在对应右奇异向量的投影给出，并由对应的奇异值进行放缩。下图给出了对雅克比均值SVD的分析。

图5

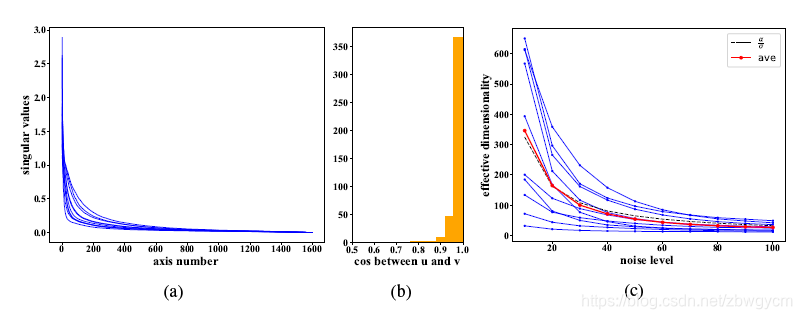
从图5（a）可以看到，大多数的奇异值都是非常接近于0，说明网络将输入图像的的大多数成分都抛弃了，只保留了一个非常低维的部分。从图5（b）可以看到对应于同一个不可忽略的奇异值（奇异值比较大）的左右奇异向量是近似相同的。这说明雅克比矩阵是近似对称的，可以将其解释为网络将噪声信号投影到了一个低维子空间，正如小波阈值降噪法一样。下图展示了左特征向量（$U_i$）的可视化结果，从左到右依次对应于不同的奇异值（奇异值递减）。从下图可以看出，对应于较大奇异值的奇异向量捕捉了输入图像的特征。而对应于接近于0的奇异值的奇异向量是非结构化的。

图6

定义信号空间的有效维度（effective dimensionality）为，将方差为${\sigma }^2$的N维高斯噪声向量做线性映射得到的方差经过噪声方差做归一化后的值，$d:=E_n\Vert A_{y}n{\Vert }^2/{\sigma }^2={\sum }_{i=1}^N{s}_i^2$。

当对保留的信号子空间进行测试时，发现清晰图像几乎完整地包含在内。对于输入$y:=x+n$，由维度$d$以内的奇异向量张成的子空间几乎完整包含了清晰图像$x$，这意味着将$x$投影于子空间可以保持大部分能量。

从下左图可以看到，投影于子空间所保留下的相对范数比例在噪声方差从10变到100时都接近于1。说明在每个特定的噪声水平下，信号子空间都几乎包含了清晰图像的信息。从下右图可以看到，不同噪声水平的信号子空间是嵌套的。更高的噪声水平的子空间坐标轴很大程度上位于最低噪声水平（$\sigma =10$）的子空间内。

图7

同时，从图5（c）可以看出，对于任意给定的清晰图像，信号子空间的有效维度$d$随着噪声水平同步下降。在更低的噪声水平下，网络检测到更丰富的图像特征，构建一个更大的信号子空间来捕捉和保存这些图像特征。另外还可以看到平均来说，$d$近似正比于$\frac{1}{\sigma }$。

最后，信号子空间维度的这些特性，以及其包含清晰图像信息这个事实，解释了观察到的在不同信号水平下的降噪性能。假设$d\approx \alpha /\sigma$，均方误差正比于$\sigma$：

$MSE=E_n\Vert A_y(x+n)-x{\Vert }^2\approx E_n\Vert A_{y}n{\Vert }^2\approx {\sigma }^{2}d\approx \alpha \sigma$

这也说明了如图2所示，去噪图像的PSNR与输入PSNR呈线性关系，而且即使网络在一个较小噪声范围内进行训练，上述关系依然保持。

Conclusion

作者只在高斯噪声上测试了无偏置网络的有效性，对于该模型是否适用于真实噪声和其他图像复原任务还待验证。从目前作者的实验来看，对于图像去模糊任务中的不同大小模糊核，该模型是不充分的，无法复现去噪的结论。