覆盖矩形

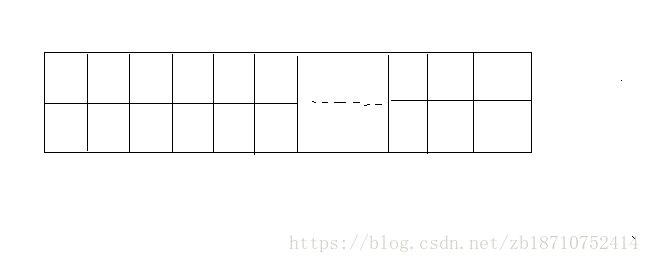
f(n)表示2*n个矩形共有f(n)种放法。

当最后一列竖着放的时候，而有f(n - 1)种放法 ；

当最后四个方格横着放时，共有f(n-2)种放法。

所有f(n) = f(n -1) +f(n-2)，即为斐波那契数列。

public class Solution {
    public int RectCover(int target) {
        if(target < 3) {
            return target;
        } else {
            int t1 = 1,t2 = 2;
            for(int i = 2; i < target; i++) {
                t2 = t1 + t2;
                t1 = t2 - t1;
            }
            return t2;
        }
    }
}