支持向量机（SVM）和python实现（一）

1. 问题的提出

若存在一个样本集，其中有两类数据，我们希望将他们分类

像上图(a)那样的样本集，SVM的目的就是企图获得一个超平面（在这个例子中超平面是一个直线），这个超平面可以完美的分割不同的数据集，我们用下面的线性方程来表示这个超平面：
$${\omega }^{\mathbf{T}}\mathbf{x}+b=0$$
对于二维空间的超平面，实际上就是：
$$\left[\begin{array}{cc}w1& w2\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]+b=0$$
我们再观察图(b)和©的两个直线，很明显b中的直线对样本集的划分更好一些，因为，在直线边缘的样本点离直线更远一些，这样就提高了样本划分的鲁棒性，所以我们就有了一个寻找超平面的最开始的理念：找到的这个超平面要离2组样本集尽量的远，即点到超平面的距离尽量大。
这里直接给出点到超平面的距离：
$$d=\frac{\left|{\omega }^T\mathbf{x}+b\right|}{\Vert \omega \Vert }$$
我们现在再给出样本的类别标签，红色点为-1，蓝色点为1，则有：
$$\{\begin{array}{cc}{\omega }^T{\mathbf{x}}_{\mathbf{i}}+b>0& y_i=1\\ {\omega }^T{\mathbf{x}}_{\mathbf{i}}+b<0& y_i=-1\end{array}$$
如果我们要求再高一些，我们希望这些点到超平面的距离都要大于d，则有：
$$\{\begin{array}{cc}({\omega }^T{\mathbf{x}}_{\mathbf{i}}+b)/\Vert \omega \Vert \ge d& y_i=1\\ ({\omega }^T{\mathbf{x}}_{\mathbf{i}}+b)/\Vert \omega \Vert \le d& y_i=-1\end{array}$$
不等式两边同时除以d，可以得到：
$$\{\begin{array}{cc}{\omega }_d^T{\mathbf{x}}_{\mathbf{i}}+b_d\ge 1& y_i=1\\ {\omega }_d^T{\mathbf{x}}_{\mathbf{i}}+b_d\le -1& y_i=-1\end{array}$$
其中
$${\omega }_d=\frac{\omega }{\Vert \omega \Vert d},b_d=\frac{b}{\Vert \omega \Vert d}$$
实际上 ${\omega }_d^T{\mathbf{x}}_{\mathbf{i}}+b_d=0$和 ${\omega }^T{\mathbf{x}}_{\mathbf{i}}+b=0$是同样的超平面，既然如此我们就把 ${\omega }_d$和 $ b_{d}$继续叫做 $\omega$和 $b$，那么我们就获得了SVM优化问题的约束条件:
$$\{\begin{array}{cc}{\omega }^T{\mathbf{x}}_{\mathbf{i}}+b\ge 1& y_i=1\\ {\omega }^T{\mathbf{x}}_{\mathbf{i}}+b\le -1& y_i=-1\end{array}\text{\hspace{1em}(1.1)}$$

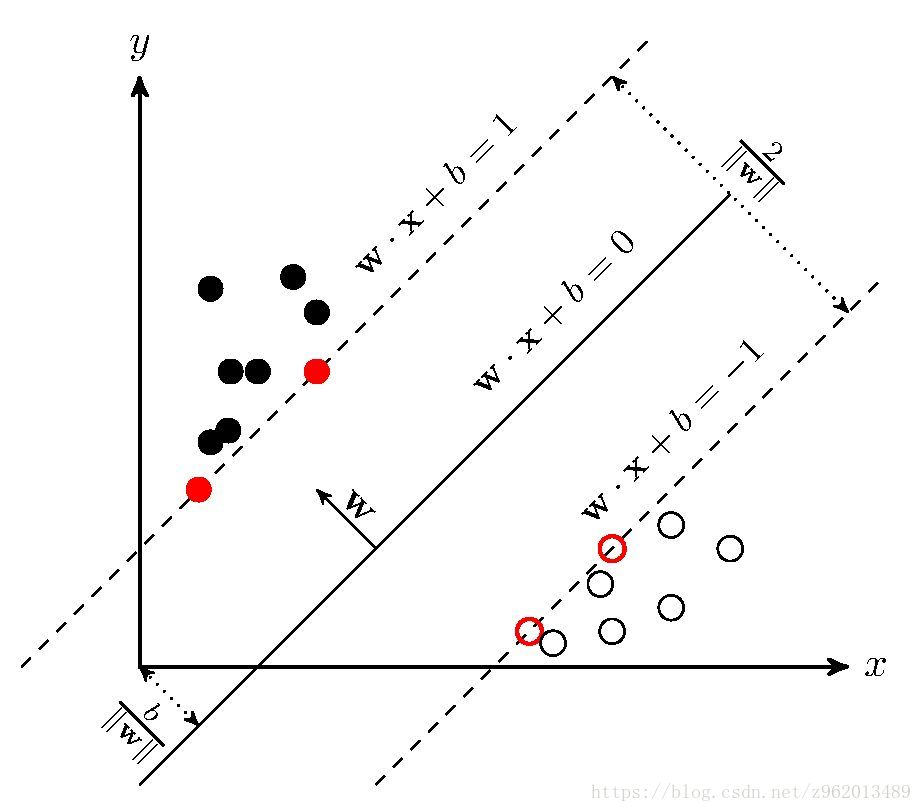
(图片来自https://www.cnblogs.com/freebird92/p/8909546.html)

如上图所示的距离超平面最近的几个训练样本点使(1.1)中的等号成立，这些点我们称为“支持向量”，两个异类支持向量到超平面的距离之和为$\frac{2}{\Vert \omega \Vert }$，我们希望这个值越大越好，即$\frac{1}{2}{\Vert \omega \Vert }^2$越小越好，所以我们的问题就变成了：
$$\begin{gathered} min\frac{1}{2}{\Vert \omega \Vert }^2 \\ s.t.y_i({\omega }^T{\mathbf{x}}_{\mathbf{i}}+b)\ge 1,i=1,2,...,m.\text{\hspace{1em}(1.2)} \end{gathered}$$

2. 对偶问题##

式(1.2)是一个凸二次规划问题，我们可以使用拉格朗日乘子法获取其对偶问题来求解，引入拉格朗日乘子${\alpha }_i\ge 0i=1,2,...,m$,则式(1.2)写为：
$$L(\omega ,b,\alpha )=\frac{1}{2}{\Vert \omega \Vert }^2+\sum _{i=1}^m{\alpha }_i(1-y_i({\omega }^T{x}_i+b))\text{\hspace{1em}(2.1)}$$
对$\omega$，b求偏导为0可得：
$$\omega =\sum _{i=1}^m{\alpha }_i{y}_i{\mathbf{x}}_{\mathbf{i}}0=\sum _{i=1}^m{\alpha }_i{y}_i\text{\hspace{1em}(2.2)}$$
将(2.2)带入(2.1)可得：
$$\begin{gathered} L(\omega ,b,\alpha )=\frac{1}{2}{\Vert \omega \Vert }^2+\sum _{i=1}^m{\alpha }_i(1-y_i({\omega }^T{x}_i+b)) \\ =\frac{1}{2}{\omega }^T\omega -{\omega }^T\sum _{i=1}^m{\alpha }_i{y}_i{\mathbf{x}}_{\mathbf{i}}+\sum _{i=1}^m{\alpha }_i-\sum _{i=1}^m{\alpha }_i{y}_{i}b \\ =\frac{1}{2}{\omega }^T(\omega -2\sum _{i=1}^m{\alpha }_i{y}_i{\mathbf{x}}_{\mathbf{i}})+\sum _{i=1}^m{\alpha }_i \\ =\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1,j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{\mathbf{x}}_{\mathbf{i}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{j}}\text{\hspace{1em}(2.3)} \end{gathered}$$
最后的对偶问题为：
$$\begin{gathered} max.\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1,j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{\mathbf{x}}_{\mathbf{i}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{j}} \\ s.t.{\alpha }_i\ge 0\sum _{i=1}^m{\alpha }_i{y}_i\text{\hspace{1em}(2.4)} \end{gathered}$$
解出$\alpha$后求出$\omega$和b就可以得到模型：
$$\begin{gathered} f(\mathbf{x})={\omega }^T\mathbf{x}+b \\ =\sum _{i=1}^m{\alpha }_i{y}_i{\mathbf{x}}_{\mathbf{i}}\mathbf{x}+b\text{\hspace{1em}(2.5)} \end{gathered}$$
因为式(1.2)含有不等式约束，因此对偶问题应满足KKT条件，这里稍微说一下KKT条件怎么获得的。

KKT条件

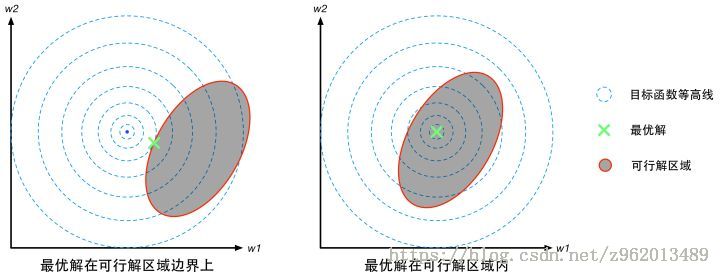
（图来自https://zhuanlan.zhihu.com/p/24638007）

不等式约束 $g(x)\le 0$即为图中的可行解区域，最优解 $x^{*} $的位置有两种情况：在可行区域边界上或者在可行区域内部。
**在边界上：**这种情况下 $g(x)=0$，目标函数$f(x)$在可行解区域边缘更大，可行解区域其他地方更小，而$g(x)$在可行解区域内小于0，外部大于0，意味着$f(x)$的梯度方向与约束条件函数$g(x)$的梯度方向相反，则在最优解处满足下式：
$$\nabla f({\mathbf{x}}^{\ast })+\lambda \nabla g({\mathbf{x}}^{\ast })=0$$
根据上式可以推出当最优解在边界上时$\lambda >0$
**在区域内：**这种情况相当于约束条件不存在，因此拉格朗日乘子$\lambda =0$，$g(x)<0$
这样就得出了KKT条件
$$\{\begin{array}{c}g(\mathbf{x})\le 0\\ \lambda \ge 0\\ \lambda g(\mathbf{x})=0\end{array}$$
其中第一个式子是约束本身，第二个式子是对拉格朗日乘子的描述，第三个式子是综合上述2种情况后获得的表达。

现在我们再回到之前的对偶问题中，(2.4）需要满足的KKT条件为：
$$\{\begin{array}{c}{\alpha }_i\ge 0\\ y_{i}f({\mathbf{x}}_{\mathbf{i}})-1\ge 0\\ {\alpha }_i(y_{i}f({\mathbf{x}}_{\mathbf{i}})-1)=0\end{array}$$
于是，对于任意训练样本，总有${\alpha }_i=0$或$y_{i}f({\mathbf{x}}_{\mathbf{i}})=1$，当${\alpha }_i=0$时，该样本不会对目标函数产生影响，若${\alpha }_i>0$，则必有$y_{i}f({\mathbf{x}}_{\mathbf{i}})=1$，此时对应样本位于最大间隔边界上，是一个支持向量。

##3. 核函数##
前面我们举的例子都是线性可分的，如果找不到一条直线将两个数据集分离的时候该怎么办呢？

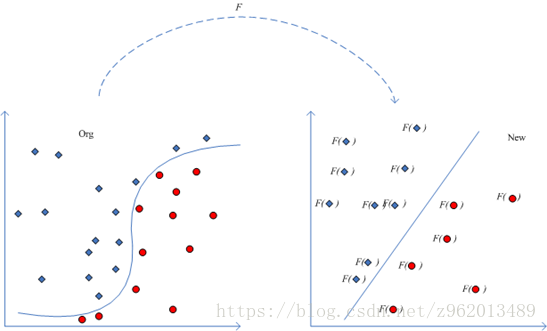
（图片来自http://www.360doc.com/content/14/0526/16/10724725_381159791.shtml）
对于这样的问题，我们可以通过将样本点从原始空间映射到一个更高维的特征空间，使在这个新的特征空间内，样本点变得线性可分，就像上图描述的那样，我们用 $\phi (\text{x})$来表示将x映射后的特征向量，于是我们就可以将模型写为：
$$\begin{gathered} f(\mathbf{x})={\omega }^T\phi (\text{x})+b \\ =\sum _{i=1}^m{\alpha }_i{y}_i\phi (\text{x}{)}^T\phi ({\mathbf{x}}_{\mathbf{i}})+b\text{\hspace{1em}(3.1)} \end{gathered}$$
对偶问题也描述为：
$$\begin{gathered} max.\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1,j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j\phi ({\text{x}}_i{)}^T\phi ({\mathbf{x}}_{\mathbf{j}}) \\ s.t.{\alpha }_i\ge 0\sum _{i=1}^m{\alpha }_i{y}_i\text{\hspace{1em}(3.2)} \end{gathered}$$
求解(3.2)涉及到计算 $\phi ({\text{x}}_i{)}^T\phi ({\mathbf{x}}_{\mathbf{j}})$考虑到样本x映射到特征空间后维数可能很高，因此直接计算 $\phi ({\text{x}}_i{)}^T\phi ({\mathbf{x}}_{\mathbf{j}})$是很困难的，为了避免这种情况，我们引入下面这样的函数：
$${\kappa }_{ij}=\kappa ({\mathbf{x}}_{\mathbf{i}},{\mathbf{x}}_{\mathbf{j}})=⟨\phi ({\mathbf{x}}_{\mathbf{i}}),\phi ({\mathbf{x}}_{\mathbf{j}})⟩=\phi ({\mathbf{x}}_{\mathbf{i}}{)}^T\phi ({\mathbf{x}}_{\mathbf{j}})$$
即${\mathbf{x}}_{\mathbf{i}}$和${\mathbf{x}}_{\mathbf{j}}$在特征空间的内积等于他们在原始样本空间中通过函数$\kappa ({\mathbf{x}}_{\mathbf{i}},{\mathbf{x}}_{\mathbf{j}})$计算的结果，于是式(3.2)就可以重新写为：
$$\begin{gathered} max.\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1,j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{\kappa }_{ij} \\ s.t.{\alpha }_i\ge 0\sum _{i=1}^m{\alpha }_i{y}_i\text{\hspace{1em}(3.3)} \end{gathered}$$
式(3.1)重写为：
$$\begin{gathered} f(\mathbf{x})={\omega }^T\phi (\text{x})+b \\ =\sum _{i=1}^m{\alpha }_i{y}_i\kappa ({\mathbf{x}}_{\mathbf{i}},\mathbf{x})+b\text{\hspace{1em}(3.4)} \end{gathered}$$
这里的 $\kappa ({\mathbf{x}}_{\mathbf{i}},{\mathbf{x}}_{\mathbf{j}})$就是核函数，显然，如果已知合适的$\phi (\mathbf{x})$，我们很容易就可以写出核函数$\kappa ({\mathbf{x}}_{\mathbf{i}},{\mathbf{x}}_{\mathbf{j}})$，但是在一个任务中我们通常都不知道$\phi (\mathbf{x})$是什么形式的，那么我们该怎么取核函数呢？

令$\chi$为输入空间，$\kappa ({\mathbf{x}}_{\mathbf{i}},{\mathbf{x}}_{\mathbf{j}})$是定义在$\chi \times \chi$上的对称函数，则$\kappa$是核函数当且仅当对于任意数据D={x1,x2,...,xm}D=\left \{ \mathbf{x_{1},x_{2},...,x_{m}} \right \}D={x1​,x2​,...,xm​}，“核矩阵”K总是半正定的：
$$K=\left[\begin{array}{ccccc}\kappa ({\mathbf{x}}_1,{\mathbf{x}}_1)& ...& \kappa ({\mathbf{x}}_1,{\mathbf{x}}_{\mathbf{j}})& ...& \kappa ({\mathbf{x}}_1,{\mathbf{x}}_{\mathbf{m}})\\ ...& ...& ...& ...& ...\\ \kappa ({\mathbf{x}}_{\mathbf{i}},{\mathbf{x}}_1)& ...& \kappa ({\mathbf{x}}_{\mathbf{i}},{\mathbf{x}}_{\mathbf{j}})& ...& \kappa ({\mathbf{x}}_{\mathbf{i}},{\mathbf{x}}_{\mathbf{m}})\\ ...& ...& ...& ...& ...\\ \kappa ({\mathbf{x}}_{\mathbf{m}},{\mathbf{x}}_1)& ...& \kappa ({\mathbf{x}}_{\mathbf{m}},{\mathbf{x}}_{\mathbf{j}})& ...& \kappa ({\mathbf{x}}_{\mathbf{m}},{\mathbf{x}}_{\mathbf{m}})\end{array}\right]$$

只要一个对称函数所对应的核矩阵半正定，他就能作为核函数使用，实际上，对于一个半正定核矩阵，总能找到一个与之对应的映射$\varphi $，换言之，任何一个核函数都隐式地定义了一个称为“再生和希尔伯特空间”的特征空间。前面说过，我们希望选取合适的核函数使样本在新特征空间内线性可分，因此特征空间的好坏对SVM的性能至关重要，下面给出一些常用的核函数：

• 线性核：${\kappa }_{ij}=\kappa ({\mathbf{x}}_{\mathbf{i}},{\mathbf{x}}_{\mathbf{j}})={\mathbf{x}}_{\mathbf{i}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{j}}$
• 多项式核：${\kappa }_{ij}=\kappa ({\mathbf{x}}_{\mathbf{i}},{\mathbf{x}}_{\mathbf{j}})={\left({\mathbf{x}}_{\mathbf{i}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{j}}\right)}^d$
• 高斯核：${\kappa }_{ij}=\kappa ({\mathbf{x}}_{\mathbf{i}},{\mathbf{x}}_{\mathbf{j}})=exp\left(-\frac{{\Vert {\mathbf{x}}_{\mathbf{i}}-{\mathbf{x}}_{\mathbf{j}}\Vert }^2}{2{\sigma }^2}\right)$
• 拉普拉斯核：${\kappa }_{ij}=\kappa ({\mathbf{x}}_{\mathbf{i}},{\mathbf{x}}_{\mathbf{j}})=exp\left(-\frac{\Vert {\mathbf{x}}_{\mathbf{i}}-{\mathbf{x}}_{\mathbf{j}}\Vert }{\sigma }\right)$
• Sigmoid核：${\kappa }_{ij}=\kappa ({\mathbf{x}}_{\mathbf{i}},{\mathbf{x}}_{\mathbf{j}})=tanh(\beta {\mathbf{x}}_{\mathbf{i}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{j}}+\theta )$

此外，还可以通过函数组合得到核函数：

• 存在2个核函数${\kappa }_1$和${\kappa }_2$，他们的线性组合$a{\kappa }_1+b{\kappa }_2$也是核函数
• 存在2个核函数${\kappa }_1$和${\kappa }_2$，他们的直积${\kappa }_1\otimes {\kappa }_2$也是核函数
• 存在核函数${\kappa }_1$，对于任意函数$g(\mathbf{x})$,$\kappa =g(\mathbf{x}){\kappa }_{1}g(\mathbf{x})$也是核函数

###传送门###
支持向量机（SVM）和python实现（二）https://blog.youkuaiyun.com/z962013489/article/details/82559626
支持向量机（SVM）和python实现（三）https://blog.youkuaiyun.com/z962013489/article/details/82622036