粒子群优化算法PSO(matlab代码)

单目标单变量的粒子群算法代码

clear
clc
%定义参数
w=2; %惯性权重
c1=1.5; %个体权重
c2=2; %社会权重
P=10; %粒子数
liter=50; %迭代次数
vmax=2;%最大速度
vmin=-2;%最小速度
limit=[-10,10]; %位置范围(自变量x的取值范围)
dim=1; %自变量维数
t=0.99;
%定义函数
Objective=@(x) x.*sin(x).*cos(2.*x)-2.*x.*sin(3.*x)+3.*x.*sin(4.*x)+x; %(定义单目标单变量的函数，可修改目标函数)
% Objective=@(x) x.^2;
%初始化种群位置和速度
x=limit(1)+(limit(2)-limit(1)).*rand(P,dim);   %初始化粒子个体位置
v=2*rand(P,dim);                               %初始化粒子速度

%初始化函数值，初始化当前个体最优和全局最优
for i =1:P
    f(i)=Objective(x(i));
end
Pbest_x=x;
Pbest_f=f;
[Gbest_f,Number]=min(Pbest_f);
Gbest_x=Pbest_x(Number);

%主循环迭代
for i=1:liter
    for j=1:P
    v(j)=w.*v(j)+c1.*rand().*(Pbest_x(j)-x(j))+c2.*rand().*(Gbest_x-x(j)); %计算粒子移动速度(方向和大小)
    if v(j)>=vmax || v(j)<=vmin     %约束速度大小不超过极限值
        v(j)=vmin+(vmax-vmin).*rand();
    end


    x(j)=x(j)+v(j);               %更新粒子的位置

    if x(j)>=limit(2) || x(j)<=limit(1)     %边界修复函数，对于超出取值范围的粒子返回随机位置
    x(j)=limit(1)+(limit(2)-limit(1)).*rand();
    end

    f_val=Objective(x);           %计算更新后的函数值(适应度)
      
    if Pbest_f(j)>=f_val(j)      %如果个体适应度更优，则更新个体的自变量和函数值
        Pbest_f(j)=f_val(j);
        Pbest_x(j)=x(j);
    end
    if Gbest_f>=Pbest_f(j)        %更新全局的最优自变量和函数值
        Gbest_f=Pbest_f(j);
        Gbest_x=Pbest_x(j);
    end
    end
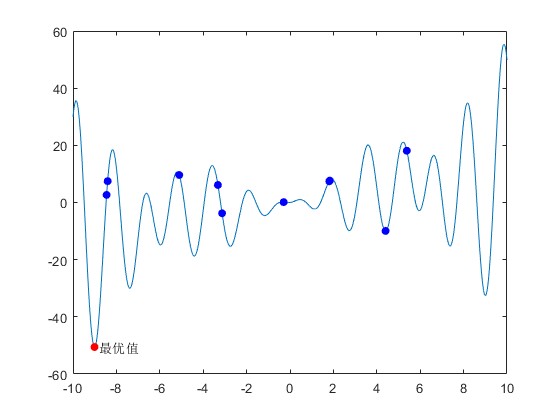
    figure(1)
    X=linspace(limit(1),limit(2),1000);
    Y=Objective(X);
    figure(1)
    plot(X,Y)
    hold on
    scatter(x,f_val,'b','filled')
    pause(0.1)
    hold off
    w=w.*t;
end
hold on
%输出结果
sprintf("当x=%d时最小函数值为%d",Gbest_x,Gbest_f)
%画图
scatter(Gbest_x,Gbest_f,'filled','r')
txt = '最优值';
text(Gbest_x+0.01*(limit(2)-limit(1)),Gbest_f,txt)

      

个人学习用