Efficient Lattice (H)IBE In The Stand Model学习记录
文章内容参考Steven Yue的知乎专栏, 博客
目录
前言
网络安全课程讲到了基于格的密码学内容,看了篇经典的IBE(Identity-Based Encryption)算法,文章提出了一种基于格(lattice)的身份加密,相较于CHKP10,该算法加密矩阵长度固定。
初识比较晦涩,因此在此处记录一下。
一、格(Lattice)的简介

Λ
=
Z
n
\Lambda =\Z^{n}
Λ=Zn
可以对整数格进行线性变换B,得到一个新的格

Λ
=
B
⋅
Z
\Lambda = B \cdot \Z
Λ=B⋅Z
lattice的基
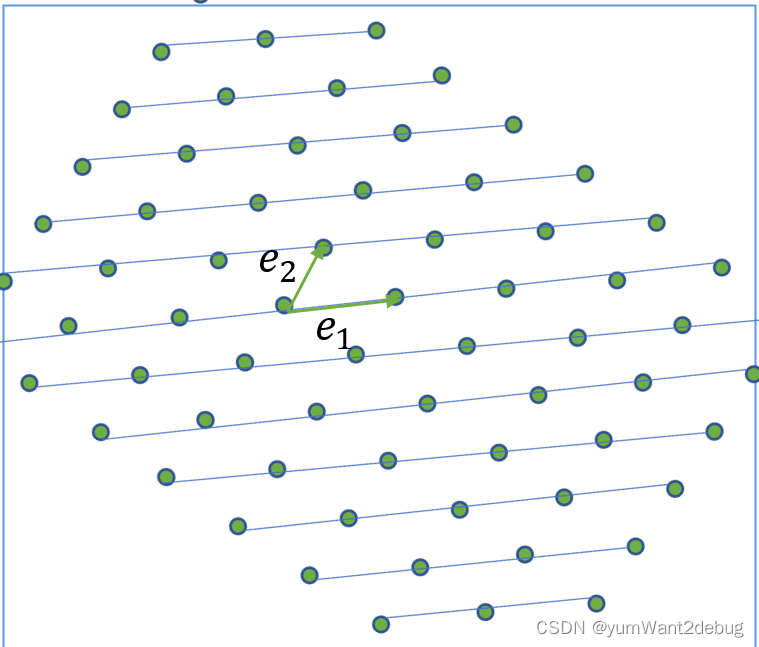 我们假设一个格拥有基向量
b
1
,
b
2
,
…
,
b
n
b_{1},b_{2},\dots,b_{n}
b1,b2,…,bn。那么这个Lattice就是它的基向量的任意线性组合的集合,我们也可以把所有基向量组合成矩阵
B
\mathbf{B}
B来表示。
我们假设一个格拥有基向量
b
1
,
b
2
,
…
,
b
n
b_{1},b_{2},\dots,b_{n}
b1,b2,…,bn。那么这个Lattice就是它的基向量的任意线性组合的集合,我们也可以把所有基向量组合成矩阵
B
\mathbf{B}
B来表示。
L
=
∑
i
=
1
n
b
i
⋅
Z
=
{
B
x
:
x
∈
Z
n
}
\mathcal{L} =\sum_{i=1}^{n}\mathbf{b_{i}}\cdot\Z=\{\mathbf{Bx:x}\in\Z^{n}\}
L=∑i=1nbi⋅Z={Bx:x∈Zn}
同理,可以通过线性代数进行基变换,得到一组新的基
C
\mathbf{C}
C

格的距离
给定点
t
\mathbf{t}
t,用
λ
\lambda
λ表示其他点与点
t
\mathbf{t}
t的距离。
一般用
λ
1
\lambda_1
λ1定义整个格中点与点之间最短的距离。
同理可得,我们也可以定义距离第二近的点距离
λ
2
\lambda_2
λ2,第三近的
λ
3
\lambda_3
λ3,一直到第n近的
λ
n
\lambda_n
λn

二、格中的难题
基于格的密码学算法具有量子抵抗性
最短向量问题(SVP,Shortest Vector Problem)
问题的定义为:给定一个基为
B
\mathbf{B}
B的Lattice
L
(
B
)
\mathcal{L}(\mathbf{B})
L(B),找到一个这个基构成的格点
B
x
:
x
\mathbf{Bx:x}
Bx:x,使得这个点距离0坐标点的距离最近。
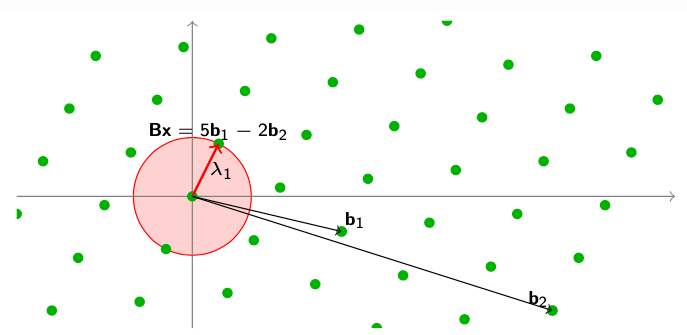
图中
λ
1
\lambda_{1}
λ1为各种点之间的最短距离。图中给出一个例子,加入我们拥有的一组格的基向量
B
=
[
b
1
,
b
2
]
\mathbf{B}=[\mathbf{b_{1},b_{2}}]
B=[b1,b2],我们可以找到一个点
B
x
\mathbf{Bx}
Bx,即
5
b
1
−
2
b
2
\mathbf{5b_{1}-2b_{2}}
5b1−2b2对应的这个点,就是这个格的最短向量
λ
1
\lambda_{1}
λ1
当我们有的基不好时,计算严格的SVP是很难的,SVP的宽松版本为:
S
V
P
γ
\mathit{SVP_{\gamma}}
SVPγ.
在
S
V
P
γ
\mathit{SVP_{\gamma}}
SVPγ中,与SVP问题区别在于要寻找的点
B
x
\mathbf{Bx}
Bx只要满足小于等于
λ
1
\lambda_{1}
λ1的一个倍数
γ
\gamma
γ就行。
∥
B
x
∥
≤
γ
λ
1
\|\mathbf{B} \mathbf{x}\| \leq \gamma \lambda_{1}
∥Bx∥≤γλ1
最近向量问题(CVP,Closest Vector Problem)
问题的定义是这样的:给定连续空间中任意的一个点
t
\mathbf{t}
t,找到距离这个点最近的格点
B
x
\mathbf{B} \mathbf{x}
Bx。
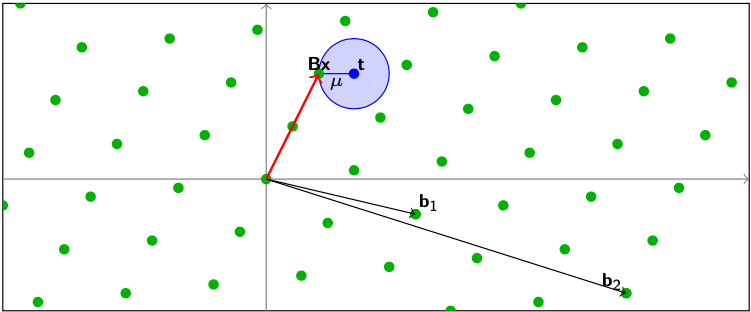
B
x
:
x
∈
Z
k
\mathbf{Bx}: \mathbf{x} \in \mathbb{Z}^k
Bx:x∈Zk
∥
B
x
−
t
∥
≤
μ
\|\mathbf{B} \mathbf{x}-\mathbf{t}\| \leq \mu
∥Bx−t∥≤μ
这里我们的约束距离
μ
\mu
μ就是这个Lattice的覆盖半径(即所有可能的[公式]中距离格点最长的距离)。同理可得,我们也可以得到CVP的宽松版,即
C
V
P
γ
\mathit{CVP_{\gamma}}
CVPγ。
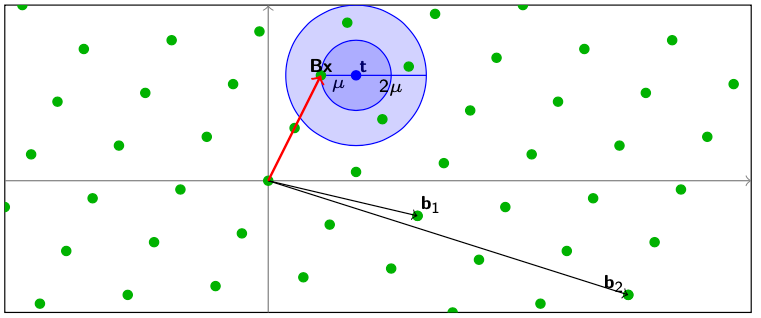
最短独立向量问题(SIVP,Shortest Independent Vectors Problem)
问题定义:给定一个Lattice
(
L
(
B
)
(\mathcal{L}(\mathbf{B})
(L(B),找到
n
n
n个线性独立的向量
B
x
1
,
…
,
B
x
n
\mathbf{Bx_1, \dots, Bx_n}
Bx1,…,Bxn并且这些向量的长度都要小于等于最长的最短向量
λ
n
\lambda_n
λn。
max
i
∣
∣
B
x
i
∣
∣
≤
λ
n
\max_i \lvert \lvert \mathbf{Bx_i} \rvert \rvert \le \lambda_n
maxi∣∣Bxi∣∣≤λn
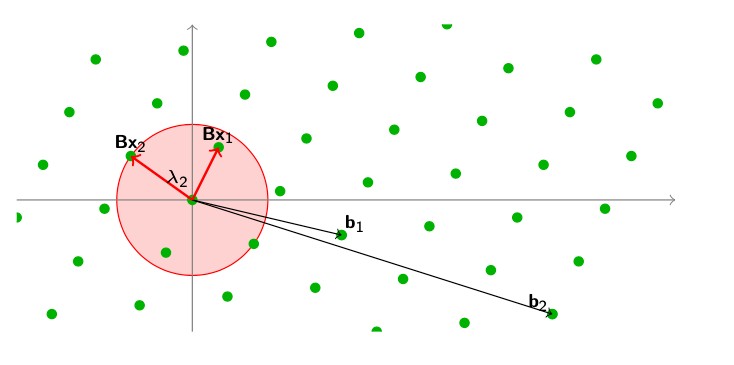
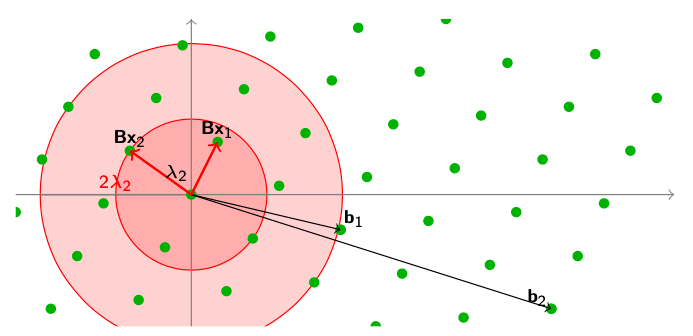
这个图就很好的表达了在(n=2)的情况下,我们找到了两个小于等于
λ
2
\lambda_2
λ2的点。和SVP与CVP问题一样,我们也可以给出SIVP问题的宽松版定义,即
S
I
V
P
γ
SIVP_\gamma
SIVPγ。在宽松版本中,我们只需要找到
γ
λ
n
\gamma \lambda_n
γλn范围内的就可以了。
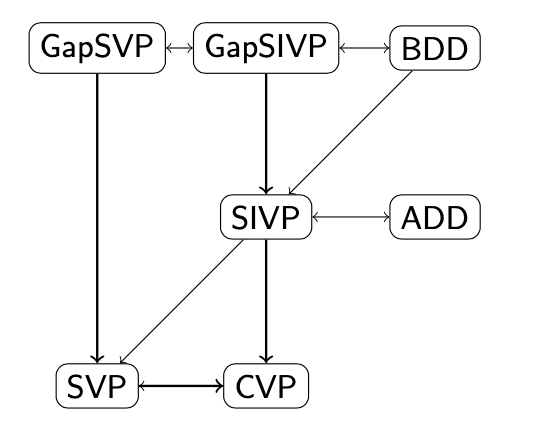
Lattice中难题的关系
LWE问题(Learning With Errors)
2005年,Regev提出基于格的LWE问题,定义如下:
首先,我们随机的选取一个矩阵
A
∈
Z
q
m
×
k
\mathbf{A} \in \mathbb{Z}_q^{m \times k}
A∈Zqm×k,一个随机向量
s
∈
Z
q
k
\mathbf{s} \in \mathbb{Z}_q^k
s∈Zqk,和一个随机的噪音
e
∈
ε
m
\mathbf{e} \in \varepsilon^m
e∈εm。我们定义一个LWE系统的输出
g
A
(
s
,
e
)
g_\mathbf{A}(\mathbf{s, e})
gA(s,e)为:
g
A
(
s
,
e
)
=
A
s
+
e
mod
q
g_\mathbf{A}(\mathbf{s, e}) = \mathbf{As + e} \text{ mod }q
gA(s,e)=As+e mod q
一个LWE问题就是,给定一个矩阵
A
\mathbf{A}
A,和LWE系统的输出
g
A
(
s
,
e
)
g_\mathbf{A}(\mathbf{s, e})
gA(s,e),还原
s
s
s。
如果噪音
e
\mathbf{e}
e是0的话,那么LWE系统输出的
A
s
\mathbf{As}
As其实就是Lattice
Λ
(
A
T
)
\Lambda(\mathbf{A^T})
Λ(AT)中的一个格点。这也就是说,加入噪音不是0的话,那么我们得到的结果就是在
Λ
\Lambda
Λ的某个格点附近的一个向量。这个时候,我们就只需要求解CVP问题,就可以还原出这个格点了。
Regev定义LWE问题的困难度是基于最坏情况的SIVP困难度的。
三、格中的陷门
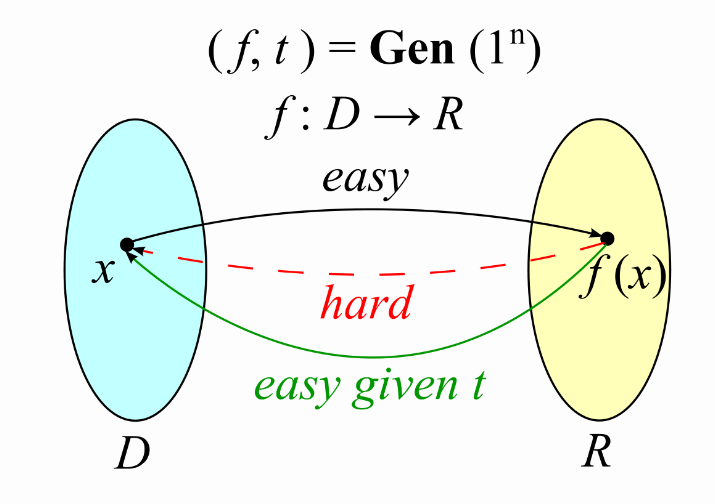
Trapdoor Function(TDF),即陷门函数,是一个密码学中非常常见的一个基础工具。
如果只知道这个函数的本身,那么这个函数就是一个单向函数(OWF)。就是给定一个输入
x
x
x,可以快速地计算
f
(
x
)
f(x)
f(x)。但是如果只知道这个函数的输出
f
(
x
)
f(x)
f(x)的话,我们很难从这个值推算出原本输入
x
x
x的值来。
TDF特殊之处在于,在生成一个TDF实例时,会额外产生这个函数的一个陷门Trapdoor t。如果不知道t,那么TDF是一个单向函数,如果知道Trapdoor t,那么TDF的单向性就被打破,可以有效地从
f
(
x
)
f(x)
f(x)还原
x
x
x。
四、高效的IBE
ABB10是由Agrawal,Boneh与Boyan三位在2010年提出,不同于CHKP10,它的加密矩阵 F i d \mathbf{F_{id}} Fid是恒定大小的,并不会随着 I D ID ID的长度变长而变大。
算法步骤
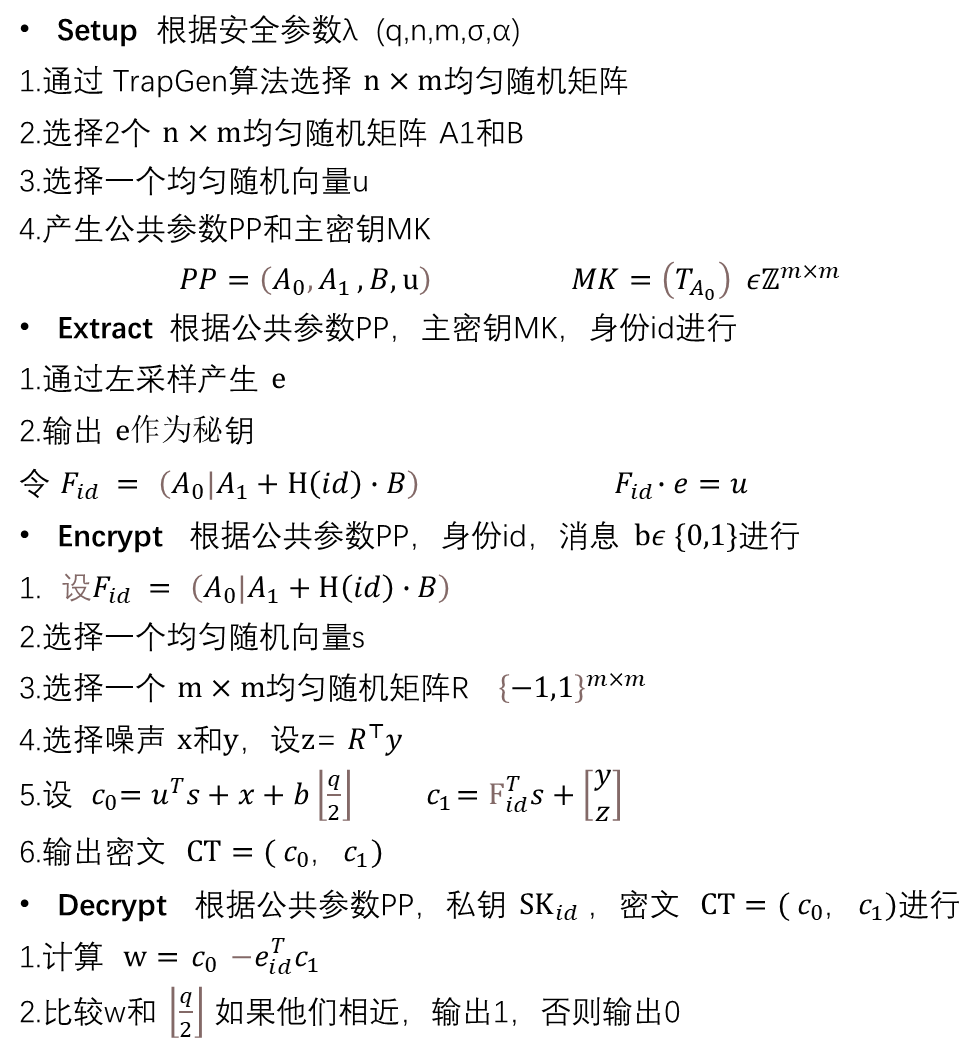
直觉上证明

这里关于为什么
T
B
T_{B}
TB也是
B
′
B'
B′的陷门是由于通过工具矩阵得到看似随机分布的矩阵,构造LWE问题的陷门函数。
具体参见第二类格陷门
安全性规约
这里采用混合论证(Hybrid Argument)的方法
- 要证明 EXP(0) 和 EXP(1) 是不可区分的,要像前文那样,构造一系列中间实验,如EXP(0.1)、EXP(0.2)。
- 证明两个相邻实验之间都是不可区分的。
- 根据不可区分的传递性,归纳出 EXP(0) 和 EXP(1) 之间是不可区分的。
前文定理正式写法的框架如下:
1. 构造如下四个实验:
实验 EXP(0):该实验即为语义安全性模型中的实验 EXP(0)。
实验 EXP(0.1):该实验与 EXP(0) 相似,所不同的是,挑战者收到攻击者发送的明文后,产生一个随机序列 r,并返回密文 c=r⊕m0。
实验 EXP(0.2):该实验与 EXP(0.1) 相似,所不同的是,挑战者返回密文 c=r⊕m1。
实验EXP(1):该实验即为语义安全性模型中的实验 EXP(1)。
2. 分别证明推论1、推论2和推论3,以证明相邻两个实验之间是不可区分的。
推论1:如果G是安全的PRG,则EXP(0)和EXP(0.1)是计算上不可区分的。
推论2:EXP(0.1)和EXP(0.2)是计算上不可区分的。
推论3:如果G是安全的PRG,则EXP(0.2)和EXP(1)是计算上不可区分的。
推论1的证明上节已给出。
推论2的证明不需要利用反证法,只需要利用一次一密完善保密性的定义,得出的结论就是任何攻击者区分EXP(0.1)和EXP(0.2)的优势都等于零。
推论3的证明和推论1的完全相同,至于为什么,前文已经说过。
3. 归纳总结攻击者区分EXP(0)和EXP(1)的优势,得出结论:对于任意概率多项式时间的攻击者,该优势是可忽略的。
至此,证明结束。
Game 0
这是定义中针对我们方案的攻击者A与INDr-sID-CPA挑战者之间的原始INDr-sID-CPA博弈。
Game 1
改变公共参数𝐴_1,设
i
d
∗
id^{*}
id∗是𝒜想攻击的身份,
令
A
1
⟵
A
0
R
∗
−
H
(
i
d
∗
)
B
A_{1} \longleftarrow A_{0} R^{*}-H\left(\mathrm{id}^{*}\right) B
A1⟵A0R∗−H(id∗)B 其余部分不变
𝑅
∗
𝑅^{∗}
R∗仅在构建𝐴_1和构建挑战密文时使用,根据引理,在𝒜视角,
𝐴
0
𝐴_{0}
A0
𝑅
∗
𝑅^{∗}
R∗ 和
𝐴
1
𝐴_{1}
A1是不可区分的。因此Game 0和 Game 1是不可区分的。
Game 2
改变
𝐴
0
𝐴_{0}
A0和
𝐵
𝐵
B的选取,
𝐴
0
𝐴_{0}
A0 为随机矩阵, 𝐵通过TrapGen产生,挑战者拥有 𝐵的陷门
𝑇
𝐵
𝑇_{𝐵}
TB,
𝐴
1
𝐴_{1}
A1的选择和Game 1中一样。
挑战者通过
𝑇
𝐵
𝑇_{𝐵}
TB 响应
ⅈ
𝑑
≠
ⅈ
𝑑
∗
ⅈ𝑑≠ⅈ𝑑^∗
ⅈd=ⅈd∗的私钥查询
F
id
:
=
(
A
0
∣
A
1
+
H
(
i
d
)
⋅
B
)
=
(
A
0
∣
A
0
R
∗
+
(
H
(
i
d
)
−
H
(
i
d
∗
)
)
B
)
F_{\text {id }}:=\left(A_{0} \mid A_{1}+H(\mathrm{id}) \cdot B\right)=\left(A_{0} \mid A_{0} R^{*}+\left(H(\mathrm{id})-H\left(\mathrm{id}^{*}\right)\right) B\right)
Fid :=(A0∣A1+H(id)⋅B)=(A0∣A0R∗+(H(id)−H(id∗))B)
[
𝐻
(
ⅈ
𝑑
)
−
𝐻
(
ⅈ
𝑑
∗
)
]
[𝐻(ⅈ𝑑)−𝐻(ⅈ𝑑^∗ )]
[H(ⅈd)−H(ⅈd∗)]是非奇异的,
𝑇
𝐵
𝑇_{𝐵}
TB也是
𝐵
′
𝐵^′
B′的陷门,挑战者可以通过SampleRight响应私钥查询
e
←
SampleRight
(
A
0
,
(
H
(
i
d
)
−
H
(
i
d
∗
)
)
B
,
R
∗
,
T
B
,
u
,
σ
)
∈
Z
q
2
m
e \leftarrow \text { SampleRight }\left(A_{0}, \quad\left(H(\mathrm{id})-H\left(\mathrm{id}^{*}\right)\right) B, \quad R^{*}, T_{B}, \quad u, \quad \sigma\right) \in \mathbb{Z}_{q}^{2 m}
e← SampleRight (A0,(H(id)−H(id∗))B,R∗,TB,u,σ)∈Zq2m
发送𝑆𝐾_𝑖𝑑=𝑒给𝒜。由于系统参数σ足够大, 𝑒在统计上分布接近Game 1。 在Game 2中获得的优势可以忽略不记。
Game 3
密文
(
𝑐
1
∗
,
𝑐
2
∗
)
(𝑐_1^∗,𝑐_2^∗ )
(c1∗,c2∗)总是随机元素, 𝒜的优势是0
通过对LWE问题归约,对于PPT敌手来说,Game 2和Game 3在计算上是无法区分的。
假设A在区分Game 2和Game 3方面具有不可忽视的优势。我们用𝒜来构造LWE算法ℬ。
LWE问题的实例是对一个秘密s,提供一个采样𝒪 可以是完全随机 或有噪声的伪随机
ℬ通过敌手𝒜区分Game 2和Game 3,过程如下:
Instance: ℬ向𝒪接收和发送请求
Targeting: 𝒜向ℬ宣布要攻击的ⅈ𝑑^∗
Setup: ℬ构建公共参数PP
1.由m个n维列向量构成𝐴_0
2.分配第0个LWE样本(到目前为止未使用)成为公共随机n维向量
3.其余公共参数即𝐴_1 和B与Game 2中一样
Queries: ℬ回答Game 2中的每个私钥提取查询
Challenge:当𝒜发送消息
𝑏
∗
∈
0
,
1
𝑏^∗∈{0,1}
b∗∈0,1, ℬ准备
ⅈ
𝑑
∗
ⅈ𝑑^∗
ⅈd∗ 的挑战密文如下:
1.令
𝑣
0
,
…
,
𝑣
𝑚
𝑣_0,…,𝑣_𝑚
v0,…,vm为LWE实例的元素,设
v
∗
=
[
v
1
⋮
v
m
]
∈
Z
q
m
v^{*}=\left[\begin{array}{c} v_{1} \\ \vdots \\ v_{m} \end{array}\right] \in \mathbb{Z}_{q}^{m}
v∗=⎣⎢⎡v1⋮vm⎦⎥⎤∈Zqm
2.隐藏消息
c
0
∗
=
v
0
+
b
∗
⌊
q
2
⌉
∈
Z
q
c_{0}^{*}=v_{0}+b^{*}\left\lfloor\frac{q}{2}\right\rceil \in \mathbb{Z}_{q}
c0∗=v0+b∗⌊2q⌉∈Zq
3.设
c
1
∗
=
[
v
∗
(
R
∗
)
⊤
v
∗
]
c_{1}^{*}=\left[\begin{array}{c} v^{*} \\ \left(R^{*}\right)^{\top} v^{*} \end{array}\right]
c1∗=[v∗(R∗)⊤v∗]
4.选择随机
r
⟵
R
{
0
,
1
}
r \stackrel{R}{\longleftarrow}\{0,1\}
r⟵R{0,1} ,r=0时,发送
𝐶
𝑇
∗
=
(
𝑐
1
∗
,
𝑐
2
∗
)
𝐶𝑇^∗=(𝑐1^∗,𝑐_2^∗ )
CT∗=(c1∗,c2∗)给敌手,r=1时,选择随机(
𝑐
1
,
𝑐
2
𝑐_1,𝑐_2
c1,c2 )并发送给敌手。
Guess:在被允许进行额外查询后, 𝒜会猜测它是在与Game 2或Game 3的挑战者互动。我们的模拟器输出𝒜的猜测,作为它试图解决的LWE挑战的答案。 模拟器判断是随机矩阵还是LWE生成的矩阵,即参加的是Game2还是Game3
总结
参考链接 https://www.zhihu.com/column/c_1190932930565013504
https://www.bilibili.com/read/cv6842798/




 本文详细介绍了格理论在身份加密(IBE)中的应用,特别是EfficientLattice(H)IBE算法,探讨了最短向量问题、最近向量问题等核心概念,涉及格中的陷门机制和高效IBE算法步骤。学习笔记还涵盖了量子抵抗性和安全性规约,以及与LWE问题的联系。
本文详细介绍了格理论在身份加密(IBE)中的应用,特别是EfficientLattice(H)IBE算法,探讨了最短向量问题、最近向量问题等核心概念,涉及格中的陷门机制和高效IBE算法步骤。学习笔记还涵盖了量子抵抗性和安全性规约,以及与LWE问题的联系。
















 682
682

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








