1,函数逼近
1、插值问题: 求一条曲线严格通过数据点
2、曲线拟合问题: 求一条曲线在一定意义下靠近数据点
2,插值问题
1、定义:
求一个简单函数φ(x)作为f(x)的近似表达式,以满足 
我们称这样的问题为插值问题; 并称φ(x)为 f (x)的插值函数; f (x)为被插函数, x0 , x1, x2, …, xn是插值节(基)点; 是插值原则。
3,插值多项式
1、定义:

求一个次数不超过n的多项式 使满足插值原则(条件) 称Pn(x)为 f (x)的n次插值多项式
2、定理:
在n+1个互异节点处满足插值原则且次数不超过n的多项式Pn(x)存在并且唯一。
注:若不将多项式次数限制为 n ,则插值多项式不唯一。
 也是一个插值多项式,其中 可以是任意多项式。
也是一个插值多项式,其中 可以是任意多项式。




5,最小二乘法
1、 定义:已知:一组实验数据(xi,yi)(i=0,1,…,m),且观测数据有误差
求:自变量x与因变量y之间的函数关系y=F(x) ,不要求y=F(x)经过所有点,而只要求在给定点上误差 按某种标准最小。
2、 度量标准:
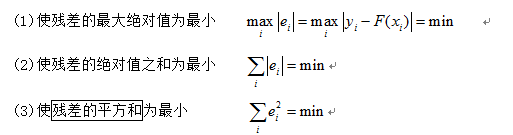











 本文探讨了函数逼近中的插值问题与曲线拟合,详细解释了插值多项式的概念及最小二乘法的应用,旨在帮助读者理解如何通过数学方法找到最接近数据点的函数表达式。
本文探讨了函数逼近中的插值问题与曲线拟合,详细解释了插值多项式的概念及最小二乘法的应用,旨在帮助读者理解如何通过数学方法找到最接近数据点的函数表达式。
















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








