并查集 L2-048

最新推荐文章于 2025-12-26 16:25:00 发布

原创最新推荐文章于 2025-12-26 16:25:00 发布 · 354 阅读

4 ·

CC 4.0 BY-SA版权

文章标签：

#算法

并查集是一种用于处理不交集问题的数据结构，以及一些图的连通操作
find 操作 $→O(1)\rightarrow O(1)$
union 操作 $n)O(n\;log\;n)$

L2-048

编码

对地图中的每一组 $(i, j)$ ，可以不重复地表示为 $i×m+ji\times m+j$ 的形式。

解码

同样地，对一个 $i×m+ji\times m+j$ ，也可以得到唯一的
$m\begin{cases}i=\frac{v}{m}\\j=i\bmod m\end{cases}$
至此，我们可以使用一个数 $n$ 来唯一表示地图矩阵中的一点，这么做是为了避免在并查集中使用 pair 存储点坐标。

总体思路

通过并查集表示各个岛屿，并且在处理并查集的过程中同步记录各个连通块中的最大值。最后遍历各个并查集的内容确定岛屿和宝藏数量。
为了避免超时，需要使用路径压缩优化查询的时间复杂度。

偏移量搜索周围元素

定义偏移量数组 $d_x=\{-1,0,1,0\},d_y=\{0,1,0,1\}$ ，表示上下左右四个方向。
|300
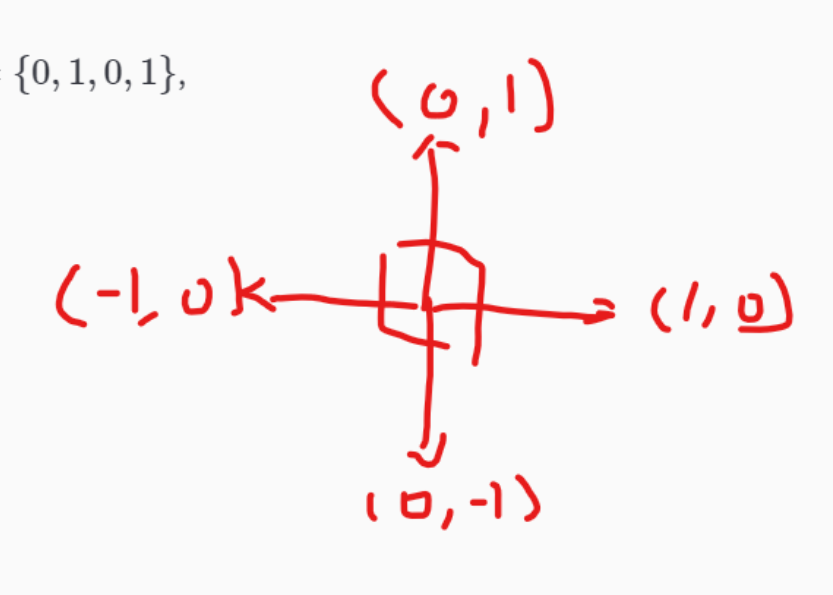
注意在循环更新坐标的时候要检查是否越界。

路径压缩

int find(int u){//路径压缩
    return u == p[u] ? p[u] : (p[u] = find(p[u]));
}

这个就是检查当前值是否等于特征节点的值，如果是，则将 u 设为 p[u]，中断递归，否则将其设置为其父节点（也就是 p[u] 的值），向上搜索直到根节点为止。
这个 find 函数最终会返回根节点的值，再将根节点和当前节点直接连通即可。

#include <bits/stdc++.h>
using namespace std;

vector<int> p;
vector<char> mx;//宝藏

int find(int u){//路径压缩
    return u == p[u] ? p[u] : (p[u] = find(p[u]));
}

int n,m;
vector<string> g;
int dx[] = {-1,0,1,0};
int dy[] = {0,1,0,-1};

int main(){
    cin >> n >> m;
    g.resize(n);//地图
    p.resize(n*m);//标记地图上每个岛屿点的根节点
    mx.resize(n*m);//把岛屿的父节点标记成宝藏的值
    

    for(auto &s : g) cin >> s;//读入地图
    for(int i = 0;i<n*m;i++){
        p[i] = i;
        mx[i] = g[i / m][i % m];//根绝地图特征值确定坐标，mx如果
    }//初始化并查集，令其特征节点均为自身
    for(int i = 0;i<n;i++){
        for(int j = 0;j<m;j++){
            if(g[i][j] == '0'){
                continue;
            }
            //陆地上下左右合并联通块
            int u = i*m + j;//确定坐标特征值
            for(int k = 0;k<4;k++){
                int ni = i + dx[k], nj = j + dy[k];
                if(ni < 0 || ni >= n || nj < 0 || nj >= m) continue;//越界
                int v = ni*m + nj;//当前检查的坐标的特征值
                if(g[ni][nj] != '0'){
                    u = find(u);//找该节点所在路径上的根节点，压缩当前路径
                    v = find(v);
                    if(u != v){//还未合并入当前连通块，合并之
                        p[u] = v;
                        mx[v] = max(mx[u], mx[v]);//标记宝藏节点
                    }
                }
            }
        }
    }

    int num_cc = 0,num_t = 0;
    for(int i = 0;i<n*m;i++){
        if(p[i] == i){
            int x = i / m;
            int y = i % m;
            if(g[x][y] != '0'){
                num_cc++;
                if(mx[i] > '1'){
                    num_t++;
                }
            }
        }
    }
    cout << num_cc << " " << num_t;
}