【中等】力扣算法题解析LeetCode141：环形链表

关注文末的名片达文汐，回复关键词“力扣源码”，即可获取完整源码！！详见：源码和核心代码的区别

题目详情

给你一个链表的头节点 head，判断链表中是否有环。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

如果链表中存在环，则返回 true；否则，返回 false。

示例 1：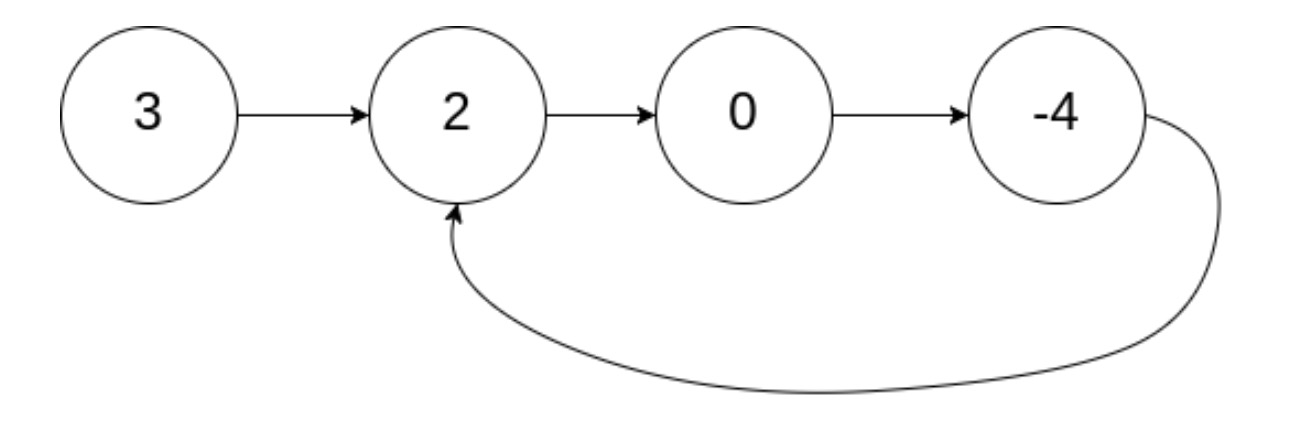

输入：head = [3,2,0,-4], pos = 1
输出：true
解释：链表中有一个环，其尾部连接到第二个节点。

示例 2：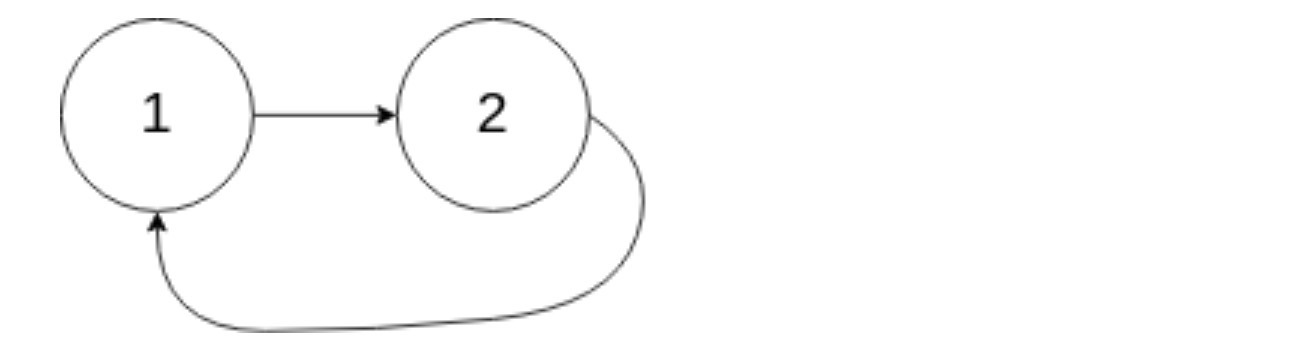
输入：head = [1,2], pos = 0
输出：true
解释：链表中有一个环，其尾部连接到第一个节点。

示例 3：

输入：head = [1], pos = -1
输出：false
解释：链表中没有环。

提示：

• 链表中节点的数目范围是 [0, 10^4]
• -10^5 <= Node.val <= 10^5
• pos 为 -1 或者链表中的一个有效索引。

进阶： 你能用 O(1)（即，常量）内存解决此问题吗？

---

解题思路

最优解法：快慢指针（Floyd 判圈算法）

• 核心思想：使用两个指针，慢指针每次移动一步，快指针每次移动两步。如果链表存在环，快指针最终会追上慢指针（相遇）；如果无环，快指针会先到达链表尾部（null）。
• 时间复杂度：O(n)。
  • 当链表无环时，快指针遍历一次链表即可结束。
  • 当链表有环时，快慢指针会在慢指针完成第一圈前相遇（具体分析见下文）。
• 空间复杂度：O(1)。仅使用两个指针，常数空间。
• 正确性分析：
  1. 无环情况：快指针会先到达链表尾部（fast == null 或 fast.next == null），返回 false。
  2. 有环情况：设环外长度为 a，环内长度为 b。慢指针进入环时，快指针已在环内，且此时快指针落后慢指针的距离为 b - (a mod b)。由于快指针每次比慢指针多走一步，两者会在 b / gcd(1, b) 步内相遇。

为什么快指针每次走两步？

• 两步能保证在 O(n) 时间内完成检测，且空间最优。若步长更大（如三步），可能增加复杂度但不会提升效率。

---

代码实现（Java版）

public class Solution {
    public boolean hasCycle(ListNode head) {
        if (head == null) {
            return false;  // 空链表直接返回false
        }
        ListNode slow = head;  // 慢指针，每次移动一步
        ListNode fast = head;  // 快指针，每次移动两步
        
        while (fast != null && fast.next != null) {
            slow = slow.next;           // 慢指针移动一步
            fast = fast.next.next;      // 快指针移动两步
            
            if (slow == fast) {          // 快慢指针相遇，说明有环
                return true;
            }
        }
        return false;  // 快指针到达链表尾部，无环
    }
}

---

代码说明

1. 初始化指针：
   • 慢指针 slow 和快指针 fast 均从链表头节点 head 开始。
2. 循环条件：
   • 判断 fast != null && fast.next != null，确保快指针能安全移动两步。
3. 移动逻辑：
   • 慢指针每次移动一步：slow = slow.next。
   • 快指针每次移动两步：fast = fast.next.next。
4. 相遇检测：
   • 若 slow == fast，说明快指针追上慢指针，存在环，返回 true。
5. 退出条件：
   • 若快指针到达链表末尾（fast 或 fast.next 为 null），说明无环，返回 false。

---

提交详情（执行用时、内存消耗）

我的名片👇👇👇👇👇👇👇👇👇👇👇