快速傅里叶变换与快速数论变换

在拉格朗日插值法与牛顿插值多项式
中有说明当给定n+1个点值序列$(x_0,y_0)，(x_1,y_1)，\cdot \cdot \cdot ，(x_n,y_n)$，其中任意两个$x$都互不相同时，有且只有一个n次多项式函数包含这些点值，换句话说，一个n次多项式可以由$n+1$个点值来表示，如果我们需要获取一个多项式的点值表示，只需要选取$n+1$个互不相同的$x$代入即可，这样做的复杂度是O(n^2)，有没有可能更快呢？考虑代入单位复数根$e^{2\pi i/n}$，选择单位复数根代入获取点值表示的这样一种方式，和离散傅里叶变换(DFT)完全相同，或者说这就是离散傅里叶变换，采用快速傅里叶变换(FFT)可以将DFT复杂度降低至O(nlogn)，也就是说可以采用快速傅里叶变换将多项式点值表示的复杂度降至O(nlogn)

快速傅里叶变换

设已有的一个多项式函数为$P(x)=a_0+a_{1}x+a_2{x}^2+\cdot \cdot \cdot +a_n{x}^n$，$w_n^i=e^{2\pi i/n}$，n是已知的要变换的序列的长度，并且一般限制为2的幂次，如果多项式的次数不够，就往后补一些系数为0的幂次。现在我们的目的是获取点值序列：$$(P(w_n^0),P(w_n^1),P(w_n^2),\cdot \cdot \cdot ,P(w_n^{n-1}))$$
$P(w_n^i)={\sum }_{j=0}^n{a}_j(w_n^i{)}^j$，这样算完整个序列显然复杂度为$O(n^2)$，考虑将这个求和式按照奇偶性分组：$$P(w_n^i)=\sum _{j=0}^{\frac{n}{2}-1}{a}_{2j}(w_n^i{)}^{2j}+\sum _{j=0}^{\frac{n}{2}-1}{a}_{2j+1}(w_n^i{)}^{2j+1}$$
由于复数根有性质：$w_n^i=w_{\frac{n}{2}}^{\frac{i}{2}}$，$(w_n^i{)}^{2j+1}=(w_n^i)(w_n^i{)}^{2j}=w_n^i{w}_{\frac{n}{2}}^{ij}$
因此：$$P(w_n^i)=\sum _{j=0}^{\frac{n}{2}-1}{a}_{2j}{w}_{n/2}^{ij}+w_n^i\sum _{j=0}^{\frac{n}{2}-1}{a}_{2j+1}{w}_{n/2}^{ij}$$
还有性质：$w_n^{n/2}=e^{\pi }=-1,$$(w_n^i{)}^{2j+n/2}=(w_n^{n/2}(w_n^i{)}^{2j})=-(w_n^i{)}^{2j}$
因此$$P(w_n^{i+n/2})=\sum _{j=0}^{\frac{n}{2}-1}{a}_{2j}(w_n^{i+n/2}{)}^{2j}+w_n^{i+n/2}\sum _{j=0}^{\frac{n}{2}-1}{a}_{2j+1}(w_n^{i+n/2}{)}^{2j}$$ $$=\sum _{j=0}^{\frac{n}{2}-1}{a}_{2j}(-w_n^i{)}^{2j}-w_n^i\sum _{j=0}^{\frac{n}{2}-1}{a}_{2j+1}(-w_n^i{)}^{2j}$$ $$=\sum _{j=0}^{\frac{n}{2}-1}{a}_{2j}(w_n^i{)}^{2j}-w_n^i\sum _{j=0}^{\frac{n}{2}-1}{a}_{2j+1}(w_n^i{)}^{2j}$$ $$=\sum _{j=0}^{\frac{n}{2}-1}{a}_{2j}{w}_{n/2}^{ij}-w_n^i\sum _{j=0}^{\frac{n}{2}-1}{a}_{2j+1}{w}_{n/2}^{ij}$$

可以发现，如果说算出$A={\sum }_{j=0}^{\frac{n}{2}-1}{a}_{2j}{w}_{n/2}^{ij}$和$B={\sum }_{j=0}^{\frac{n}{2}-1}{a}_{2j+1}{w}_{n/2}^{ij}$，那么就可以直接得到两个要求的值$P(w_n^i)=A+w_n^{i}B$和$P(w_n^{i+n/2})=A-w_n^{i}B$，也就是说在计算$P(w_n^i)$时，就可以顺带计算出$P(w_n^{i+n/2})$。因此我们应当采用计算$A$和$B$的方式，那么观察一下$A$和$B$，它们的形式与计算$P(w_n^i)$完全相同，并且输入的规模减少了一半！也就是说现在将一个大问题划分为了规模减半的两个子问题，这两个子问题的形式与大问题完全相同，因此可以继续递归计算，具个具体的例子：假如现在n=8，要求$$(P(w_n^0),P(w_n^1),P(w_n^2),\cdot \cdot \cdot ,P(w_n^7))$$采用这个算法的子问题划分应该是：
$P(w_n^0)$和$P(w_n^4)$：通过代入$w_n^0$，得到对应的A，B然后将A，B的结果合并得到$P(w_n^0)$和$P(w_n^4)$
$P(w_n^1)$和$P(w_n^5)$：通过代入$w_n^1$，得到对应的A，B然后将A，B的结果合并得到$P(w_n^1)$和$P(w_n^5)$
$P(w_n^2)$和$P(w_n^6)$：通过代入$w_n^2$，得到对应的A，B然后将A，B的结果合并得到$P(w_n^2)$和$P(w_n^6)$
$P(w_n^3)$和$P(w_n^7)$：通过代入$w_n^3$，得到对应的A，B然后将A，B的结果合并得到$P(w_n^3)$和$P(w_n^7)$
以上是算法运行的最上一层
因此这个算法的复杂度应该满足：$$T(n)=2T(n/2)+O(n)=O(nlogn)$$

FFT的递归实现：

//epsilon 用到的复数根
//buffer 需要变换的序列 如果变换的是实数序列 那么虚部全为0
//n序列的长度
//step初始为1 表示w的变化幅度 
//offset表示当前处理的子序列的偏移量
void fft(complex<double> * epsilon, complex<double> * buffer, int n, int step, int offset)
{
	if (n == 1)
	{
		return;
	}
	int m = n >> 1;
	fft(epsilon, buffer, m, step << 1, offset);
	fft(epsilon, buffer, m, step << 1, offset + step);
	for (int i = 0; i < m; i++)
	{
		int pos = 2 * i * step;
		//相应的A和B 保存在了buffer[offset+pos] 和 buffer[offset+pos+step]中
		tmp[i] = buffer[offset + pos] + epsilon[i * step] * buffer[offset + pos + step];
		tmp[i + m] = buffer[offset + pos] - epsilon[i * step] * buffer[offset + pos + step];
	}
	for (int i = 0; i < n; i++)
	{
		buffer[offset + i * step] = tmp[i];
	}
}

如果对于上述递归过程理解还是有一些困难，就自己举一个实例，手动写一遍运行过程来理解。

FFT的迭代实现
$n=16$时的迭代执行过程如图：

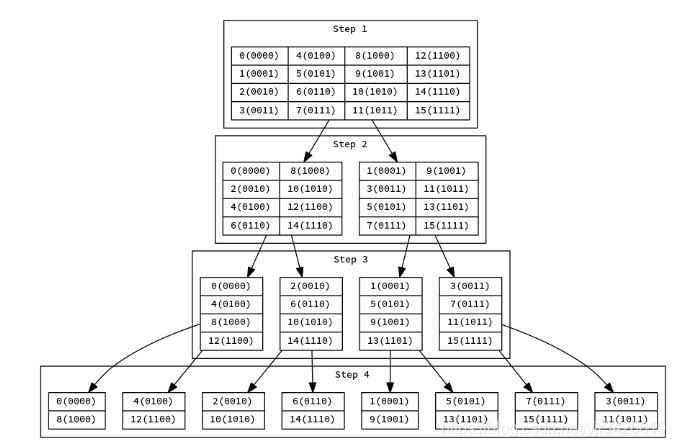
因为在每一轮执行的过程中，都是将当前的序列中取出其奇数项划分到一组去计算A，然后取出偶数项到一组去计算B，经过观察可以发现在第i轮中被划分到同一组的应该在其二进制表示中最后的i位数完全相同。
如果现在要迭代实现这个算法的话，最好是要将最末一层划分在同一组的两项在原本的序列中调整到相邻位置，比如上图中是将最初的系数序列调整为$(a_0,a_8,a_4,a_{12},a_2,a_{10},a_6,a_{14},a_1,a_9,a_5,a_{13},a_7,a_{15},a_3,a_{11})$，这样就可以直接一层一层地向上合并。
而再仔细看这张图可以发现，如果我们将这些项的二进制表示全部反转，那么它们就是$(a_0,a_1,a_2,\cdot \cdot \cdot ,a_{15})$，因此调整的方式就是将每一项放到其二进制反转后的项的位置。

FFT的迭代实现：

void bit_reverse(int n, complex<double> * x)
{
	for (int i = 0, j = 0; i < n; i++)
	{
		if (i > j) swap(x[i], x[j]);
		for (int l = n >> 1; (j ^= l) < l; l >>= 1);//二进制反转加法 从最高位开始加
	}
}

void fft_transform(complex<double> * epsilon, complex<double> * buffer, int n)
{
	bit_reverse(n, buffer);
	for (int i = 2; i <= n; i <<= 1)
	{
		int m = i >> 1;
		for (int j = 0; j < n; j += i)
		{
			for (int k = 0; k < m; k++)
			{
				complex<double> z = buffer[k + j + m] * epsilon[n / i * k];
				buffer[k + j + m] = buffer[k + j] - z;
				buffer[k + j] += z;
			}
		}
	}
}

快速傅里叶逆变换
在离散逆傅里叶变换的运算中，只需要将复数根的指数全部乘上-1，其他的过程与离散傅里叶变换完全相同，但是要在最后将所得到的结果除以N，因此快速傅里叶逆变换也只需更改复数根的指数，其余与FFT完全相同，在最后将得到的序列全部除以N即可，在O(nlogn)的时间内可以将点值序列变换回原序列。

利用FFT算法，可以加速多项式的点值表示，在离散傅里叶变换中有介绍由于复数根具备的正交性，两个序列在经过离散傅里叶变换后做乘法，就相当于原序列做卷积 并且再将结果都扩大N倍（N为序列长度），因此FFT算法可以用来加速任何需要用到卷积的算法，比如多项式相乘，多项式乘法直接相乘的复杂度为$O(n^2)$，而如果先利用FFT在O(nlogn)内得到其点值表示，在将点值对应相乘(O(n))，然后再将其在O(nlogn)内变换回系数即可。

快速数论变换

在FFT中，利用复数根的性质
1.对任意$0<=i<j<=n-1$，$w_n^i̸=w_n^j$
2.$w_n^i=w_{n/2}^{i/2}$
3.$w_n^{n/2}=e^{\pi }=-1$

将大问题划分为子问题降低复杂度，但是复指数的运算难免会有一些误差，如果我们希望在处理整数序列的时候能够避免精度的损失，就可以采用快速数论的方式。在数论中，存在一个叫做原根的东西，它也具有复数根的这些性质，如果对于数论完全没什么了解，建议先去查阅相关资料，这里简要介绍一下相关概念 ：

原根：设$a,p$互素，若使得$a^m\equiv 1(modp)$的最小正整数m为$\varphi (p)$，那么就称$a$是p的原根。
其中$\varphi (p)$为欧拉函数，表示小于p的正整数中与p互素的整数的个数，当$p$是素数时，其值为$p-1$

原根存在性：当且仅当$n=2,4,p^a,2p^a$其中p为奇素数时，n存在原根
现在取素数$p=k\cdot 2^m+1$，并且找到其原根$g$
设$g_n=g^{(p-1)/n}$(n为进行点值变换的序列长度)，现在来对应复数根的性质来看原根：
1.$设1<=i<j<=(p-1)/n$，若$g_n^i\equiv g_n^j(modp)$则$g_n^i\equiv g_n^i(g_n^{j-i})modp$，由于$(g_n^i,p)=1$，因此$g_n^{j-i}\equiv 1modp$，因此存在一个比$p-1$更小的$m$使得$g^m\equiv 1modp$，这与原根的定义矛盾，因此$g_n^{i}modp$与$g_n^{j}modp$一定不相同。
2.$g_{n/2}^{i/2}=g^{\frac{(i/2)(p-1)}{n/2}}=g^{\frac{i(p-1)}{n}}=g_n^i$
3.$g_n^{n/2}=g^{\frac{p-1}{2n}}$，$(g_n^{n/2}{)}^2=g^{\frac{p-1}{n}}\equiv 1modp$，而同余方程$x^2\equiv 1modp$只有1和-1两个解，而又由性质1，可知$g_n^{n/2}modp$只能为-1

也就是说原根也满足和单位复数根的那三条性质，因此在做求点值表示的时候，可以选择代入原根，将$w_n^i$替换为$g_n^i$，然后所有的运算都在模P的意义下进行，所有的除法转换为乘上模P意义下的逆元。

快速数论变换实现：

typedef long long ll;
const ll p = 1004535809;
const int g = 3;
//取素数p 原根为g
ll fast_pow(ll p, ll g, ll n)
{
	ll ans = 1;
	for (; g; g >>= 1, p = p * p % n)
	{
		if (g & 1) ans = ans * p % n;
	}
	return ans;
}

void ntf_reverse(ll * c, int n)
{
	for (int i = 0, j = 0; i < n; i++)
	{
		if (i > j) swap(c[i], c[j]);
		for (int l = n >> 1; (j ^= l) < l; l >>= 1);
	}
}

//flag=1 快速数论变换 flag=-1 快速数论逆变换
void nft_transform(int flag, int n, ll * c)
{
	ll g_p = ((flag == 1) ? g_k : p - 1 - g_k);
	ll g_n = fast_pow(g, g_p, p);
	for (int i = 0; i < n; i++)
	{
		g_data[i] = fast_pow(g_n, i, p);
	}
	ntf_reverse(c, n);
	for (int i = 2; i <= n; i <<= 1)
	{
		int m = i >> 1;
		ll wn = fast_pow(g, flag == 1 ? (p - 1) / i : (p - 1 - (p - 1) / i), p);
		for (int j = 0; j < n; j += i)
		{
			ll w = 1;
			for (int k = 0; k < m; k++)
			{
				ll z = c[j + k + m] * w % p;
				c[j + k + m] = (c[j + k] - z + p) % p;
				c[j + k] = (c[j + k] + z) % p;
				w = w * wn % p;
			}
		}
	}
	if (flag == -1)
	{
		ll inv = fast_pow(n, p - 2, p);
		for (int i = 0; i < n; i++)
		{
			c[i] = c[i] * inv % p;
		}
	}
}